코노이드

기하학에서 코노이드(그리스어: κωνς cone콘 및 -ειδδ similar similar 유사)는 지배된 표면으로, 판결(선)이 추가 조건을 충족한다.

(1) 모든 판결은 비행기인 다이렉트릭스 비행기와 평행하다.

(2) 모든 판결은 일정한 선인 축과 교차한다.

• 코노이드의 축이 다이렉트릭스 평면에 수직인 경우 코노이드(conoid)는 우측 코노이드다. 따라서 모든 판결은 축에 수직이다.

(1) 때문에 모든 코노이드는 카탈로니아 표면이며, 다음과 같이 파라메트릭적으로 나타낼 수 있다.

• ${\displaystyle \mathbf {x}(u,v)=\mathbf {c}(u)+v\mathbf {r}(u)\,}$

Any curve ${\displaystyle \mathbf {x} (u_{0},v)}$ with fixed parameter ${\displaystyle u=u_{0}}$ is a ruling, ${\displaystyle \mathbf {c} (u)}$ describes the directrix and the vectors ${\displaystyle \mathbf {r} (u)}$ are all parallel to the directrix plane. 벡터 $r{\displaystyle \mathbf{}}$(${\displaystyle u}$) ${\displaystyle \mathbf {r}(u)}$의 평면성은 다음과 같이 나타낼 수 있다$$.

${\displaystyle det}$( ${\displaystyle r\mathbf{},}$ ${\displaystyle r\stackrel{}{\mathbf{}}\stackrel{}{\mathbf{}}\dot{},}$ r ${\displaystyle \stackrel{}{\mathbf{¨}}}$)${\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle \det(\mathbf {r},\mathbf {r},${r},\mathbf ${\dot{r}},\mathbf$ {\dot${r}$ )=$0}$.

• 다이렉트릭스가 원일 경우, 코노이드를 원형 코노이드라고 한다.

코노이드라는 용어는 아르키메데스의 논문 On conoids와 spheroides에서 이미 사용되었다.

예

우측 원형 코노이드

모수 표현

${\displaystyle \mathbf {x}(u,v)=(\cosu,\sin u,\sin u,z_{0})+v(0,\leq u)\2\pi,v\in \mathb {R}}}$

x-y-평면의 단위 원을 directrix로 하고 y-z-평면에 평행한 directrix 평면을 가진 우측 원형 코노이드(conoid)를 설명한다. 그것의 축은 선$({\displaystyle x,}$ ${\displaystyle 0,}$ z ${\displaystyle {0\mathrm{}}_{}}$) ${\displaystyle \text{x}}$ ${\displaystyle \in }$ ${\displaystyle R\mathbb{}.}$ ${\displaystyle (x,0,z_{0})\ x\in \mathb {R}\ .}$이다.

특수 기능:

1. 수평면이 있는 교차점은 타원이다.
2. ${\displaystyle (}$ ${\displaystyle 1}$- ${\displaystyle {}^{}}$ 2${\displaystyle {}^{}}$)${\displaystyle }$( ${\displaystyle z}$- ${\displaystyle {z\mathrm{}}_{}}$ ${\displaystyle {}_{}{}^{}}$) ${\displaystyle {2\mathrm{}}^{}}$- y ${\displaystyle {2\mathrm{}}^{}}$ z ${\displaystyle {\mathrm{}}_{}^{}}$ ${\displaystyle 2{}_{}^{}}$= 0 ${\displaystyle (1-x^{0})^{2}-y^{2}z_{0}^{0$}=$0}$는 암묵적인 표현이다$$. 따라서 오른쪽 원형 코노이드는 4도 표면이다.
3. 케플러의 규칙은 반지름 $r{\displaystyle }$ ${\displaystyle r}$과 높이 h ${\displaystyle$ h}을$($를) 가진 오른쪽 원형 코노이드에 정확한$$ 볼륨을 부여한다. ${\displaystyle V}$= ${\displaystyle \pi \frac{}{}}$ ${\displaystyle \frac{2}{}}$ ${\displaystyle r{}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle$ V$={\tfrac {\pi }{2}}r^{2}h}$.

암시적 표현은 선$({\displaystyle x}$, ${\displaystyle 0}$, ${\displaystyle {z\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ $){\displaystyle (x,0,z_{0}})$의 포인트로도 충족된다$.$ 이러한 지점에는 접선 평면이 존재하지 않는다. 그런 점들을 단수라고 한다.

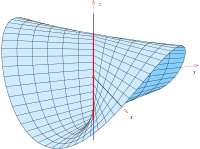
포물선 코노이드

모수 표현

${\displaystyle \mathbf {x}(u,v)=\좌측(1,u,-u^{2}\우측)+v\좌측값1,0,u^{2}\우측)}$

${\displaystyle =\좌측(1-v,u,-(1-v)u^{2}\우측)\,u,v\in \mathb {R}\,}$

$등식{\displaystyle }$ z =${\displaystyle }$- ${\displaystyle x}$ y ${\displaystyle {2\mathrm{}}^{}}$ ${\$의 포물선 코노이드 식을 설명한다$.$ 코노이드에는 다이렉트릭스로서의 포물선이 있고, 축으로서의 Y축과 다이렉트릭스 평면으로 x-z 평면에 평행한 평면이 있다. 건축가가 지붕 표면(아래)으로 사용한다.

포물선 코노이드에는 특이점이 없다.

추가 예

1. 쌍곡선 포물선 모양의
2. 플뤼커 코노이드
3. 휘트니 우산
4. 헬리코이드의

• 

  쌍곡선 포물선 모양의

• 

  플뤼커 코노이드

• 

  휘트니 우산

적용들

수학

단수점을 가진 코노이드들이 많이 있는데, 이 코노이드들은 대수 기하학에서 조사된다.

건축

다른 지배 표면과 마찬가지로 코노이드도 건축가들에게 높은 관심을 가지고 있는데, 그것은 그것들은 빔이나 바를 사용하여 건설될 수 있기 때문이다. 오른쪽 코노이드들은 쉽게 제조될 수 있다: 한 개의 나사산이 축을 따라 회전할 수 있도록 막대를 달았다. 그 후 다이렉트로 막대를 꺾어 코노이드(s. 포물선 코노이드)를 생성한다.

외부 링크

• mathworld: Plucker conoid
• "Conoid", Encyclopedia of Mathematics, EMS Press, 2001 [1994]

참조

• A. Gray, E. Abbena, S. S. Salamon, Mathematica를 사용한 곡선과 표면의 현대적 차등 기하학, 3차 에드. 2006년, FL:CRC 프레스 보카 라톤. [1] (ISBN 978-1-58488-448-4)
• 블라디미르 Y. Rovenskii, MAPLE을 사용한 곡선과 표면의 기하학 [2] (ISBN 978-0-8176-4074-3)