분할 및 변환 고유값 알고리즘

분할 및 변환 고유값 알고리즘은 최근(서클 1990년대) QR 알고리즘과 같은 전통적인 알고리즘으로 안정성과 효율성 면에서 경쟁력이 높아진 에르미트나 실제 대칭 행렬에 대한 고유값 알고리즘의 일종이다.이러한 알고리즘 뒤에 숨겨진 기본 개념은 컴퓨터 과학에서 분리-금융 접근법이다.고유치 문제는 대략 절반 크기의 두 문제로 나뉘는데, 각각은 재귀적으로 해결되며, 원래 문제의 고유치는 이러한 작은 문제의 결과로 계산된다.

여기서 우리는 1981년에 Cuppen에 의해 원래 제안되었던 것과 유사한, 분할 및 재무 알고리즘의 가장 간단한 버전을 제시한다.이 글의 범위 밖에 있는 많은 세부사항은 생략될 것이다. 그러나 이러한 세부사항을 고려하지 않으면 알고리즘이 완전히 안정적이지 않다.

배경

에르미트 행렬에 대한 대부분의 고유값 알고리즘과 마찬가지로, 분할 및 재무는 삼지각형 형태로 감소하는 것으로 시작한다.${\displaystyle m}$ ${\displaystyle \times }$ m ${\displaystyle m\time m}$ 행렬의$$ 경우, Householder reflection을 통해 4 ${\displaystyle 3m{}^{}}$ ${\frac{4$}{3}}{$3}m^{$3$$}} 부동 소수점 연산을 수행하거나, 고유 벡터가 필요한 경우 ${\displaystyle \frac{\mathrm{8m}}{}}$ $3m$ 3${$을 사용한다.아놀디 반복과 같은 다른 알고리즘들이 있는데, 이것은 특정 등급의 매트릭스에 더 도움이 될 수 있다; 우리는 여기서 더 이상 이것을 고려하지 않을 것이다.

어떤 경우에는 고유치 문제를 더 작은 문제로 압축하는 것이 가능하다.블럭 대각 행렬 고려

${\displaystyle T={\begin{bmatrix}T_{1}&0\\0&T_{2}\end{bmatrix}.}$

$T{\displaystyle }$ ${\displaystyle T}$의 고유값과 고유 벡터는 $단순히$ ${\displaystyle {T\mathrm{}}_{}}$ 1 ${\$}와$$ $T{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$}}의 값이며$,$ 이 두 가지 작은 문제를 한꺼번에 해결하는 것보다 거의 항상 더 빠를 것이다.이 기법은 많은 고유값 알고리즘의 효율성을 향상시키기 위해 사용될 수 있지만, 분할 및 조정에는 특별한 의미가 있다.

이 글의 나머지 부분에 대해서는, 분할-통화 알고리즘에 대한 $입력$은 m${\displaystyle }$× ${\displaystyle m}$ ${\displaystyle$ m$\times m}$ 실제 대칭$$ 3지각 행렬 $T{\displaystyle }$ ${\displaystyle T}$이라고 가정한다$.$ 비록 알고리즘은 은둔자 행렬에 대해 수정할 수 있지만, 여기서는 자세한 내용을 설명하지 않는다.

나누다

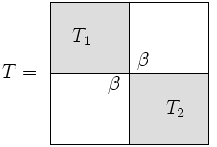
분할-분할 알고리즘의 분할 부분은 삼지각 행렬이 "거의" 블록 대각선이라는 깨달음에서 비롯된다.

The size of submatrix ${\displaystyle T_{1}}$ we will call ${\displaystyle n\times n}$, and then ${\displaystyle T_{2}}$ is ${\displaystyle (m-n)\times (m-n)}$. Note that the remark about ${\displaystyle T}$ being almost block diagonal is true regardless of how ${\d$$isplaystyle n}$이(가) 선택됨$$(즉, 매트릭스를 그렇게 분해하는 방법은 여러 가지가 있다).그러나 효율성 측면에서 n${\displaystyle n}$ m${\displaystyle }$/ ${\displaystyle 2\mathrm{}}$ $[\displaystyle n\$ 약 $m/2$}을$($를) 선택하는 것이 타당하다$.$

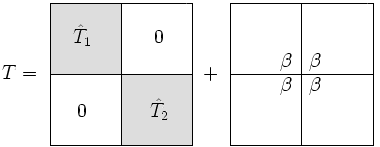
블록 대각 행렬에 $순위$ 1$$보정을 $더한$ T {\$displaystyle$ T}을$($를) 쓴다.

The only difference between ${\displaystyle T_{1}}$ and ${\displaystyle {\hat {T}}_{1}}$ is that the lower right entry ${\displaystyle t_{nn}}$ in ${\displaystyle {\hat {T}}_{1}}$ has been replaced with ${\displaystyle t_{nn}-\beta }$ and similarly, in $$${\displaystyle {\stackrel{}{T}}_{}}$^ ${\displaystyle 2_{\mathrm{}}}$ ${\$${\displaystyle {\}}_{}}$$_{$2}} 상단$$ 왼쪽 $항목{\displaystyle {}_{}}$ t ${\displaystyle {\mathrm{n}}_{}}$+${\displaystyle {}_{}}$${\displaystyle 1_{}}$, ${\displaystyle {\mathrm{n}}_{}}$ + 1 ${\$${\displaystyle {\{}_{}}$$n$${\displaystyle {+}_{}}$$1$,$n$$+$1${\displaystyle {}_{}}$n+1}-{$displaystytle t_{n+1}-\beta }$로 대체되었다$.$

The remainder of the divide step is to solve for the eigenvalues (and if desired the eigenvectors) of ${\displaystyle {\hat {T}}_{1}}$ and ${\displaystyle {\hat {T}}_{2}}$, that is to find the diagonalizations ${\displaystyle {\hat {T}}_{1}=Q_{1}D_{1}Q_{1$$}^{T}}$ and ${\displaystyle {\hat {T}}_{2}=Q_{2}D_{2}Q_{2}^{T}}$. This can be accomplished with recursive calls to the divide-and-conquer algorithm, although practical implementations often switch to the QR algorithm for small enough submatrices.

정복하다

알고리즘의 정복 부분은 비논리적인 부분이다.위에서 계산된 하위 행렬의 대각화를 고려할 때 원본 행렬의 대각화를 어떻게 찾을 수 있는가?

First, define ${\displaystyle z^{T}=(q_{1}^{T},q_{2}^{T})}$, where ${\displaystyle q_{1}^{T}}$ is the last row of ${\displaystyle Q_{1}}$ and ${\displaystyle q_{2}^{$$T}}}{{}}}{{{}}}}}$의 첫 번째 행으로$$, 이제 이 행을 보여 주는 것이 초등이다$.$

${\displaystyle T={\begin{bmatrix}Q_{1}&\\&Q_{2}\end{bmatrix}}\{bmatrix}}}\좌측({\begin{bmatrix}D_{1}&D_{2}\end{bmatrix}}+\beta z^{{{}}}}}}}}}}}}}}T}\오른쪽){\begin{bmatrix}Q_{1}^{{T}&\\&Q_{2}^{{}}T}\end{bmatrix}}$

나머지 과제는 대각 행렬의 고유값과 순위 1 보정을 찾는 것으로 축소되었다.이것을 어떻게 하는지 보여주기 전에 표기법을 단순화하자.우리는 매트릭스 $D{\displaystyle }$+ ${\displaystyle w}$ ${\displaystyle W^{}}$ ${\displaystyle {}^{}}$ ${\$ D$+w^{$$여기$서$$D$$${\displaystyle D}$은(는) 구별되는 항목이 있는 대각선이고$$ $w{\displaystyle }$ ${\displaystyle w}$은(는) 0이 아닌 항목이 있는 벡터입니다.

w가_i 0인 경우(${\displaystyle e_{}}$ i ${\$d_i)는 $D{\displaystyle }$+ ${\displaystyle w}$ ${\displaystyle {}^{}}$ ${\$d)의 고유공기다.$T}$ 이후$$${\displaystyle }$(${\displaystyle D}$+ ${\displaystyle w}$ ${\displaystyle T^{}}$) ${\displaystyle {}_{}}$ ${\displaystyle i_{}}$= ${\displaystyle d}$ e ${\displaystyle i_{}{}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle e_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\$$T}e_{i}=De_{i}=d_{i}e_{i$

$\lambda {\displaystyle }$ ${\displaystyle \lambda }$이(가) 고유 값인$$ 경우 다음을 수행하십시오.

${\displaystyle(D+www^{T}}q=\lambda q}$

여기서 $q{\displaystyle }$ ${\displaystyle q}$은(는) 해당 고유 벡터다.지금

${\displaystyle(D-\lambda I)q+w(w^{T}q)=0}$

${\displaystyle q+(D-\lambda I)^{-1w(w^{T}q)=0}$

${\displaystyle w^{T}q+w^{T}(D-\lambda I)^{-1w(w^{T}q)=0}$

$w{\displaystyle {}^{}}$ ${\displaystyle T^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle$ w$^{$$T}q}$은(는) 0이 아닌 스칼라이다.$w{\displaystyle }$ ${\displaystyle w}$도 $q{\displaystyle }$ ${\displaystyle q}$도 0이$$ 아니다.$w{\displaystyle {}^{}}$ ${\displaystyle T^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle$ w$^{$$T}q}$은(는) 0이어야 하며, $q{\displaystyle }$ ${\$$displaystyle$ $q}$은$({\displaystyle D}$+ ${\displaystyle {}^{}}$ ${\displaystyle T^{}}$ ${\displaystyle q}$= ${\displaystyle \lambda }$ ${\displaystyle q}$ ${\displaystyle(D+w^){$$T}q=\lambda q$ 그렇다면 $q{\displaystyle }$ ${\displaystyle d}$은(는) 구별되는 대각선이기$$ 때문에 q {\$displaystyle$ $q$$}$은(는) 0이 아닌 하나의 위치만 포함할 것이고$$, 따라서 내부 $제품$은 ${\displaystyle T^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle$ w$^{$$T}q}$은(는) 결국 0일 수 없다$$.따라서 다음과 같은 이점이 있다.

${\displaystyle 1+w^{T}(D-\lambda I)^{-1}w=0}$

스칼라 방정식으로 쓰이거나

${\displaystyle 1+\sum _{j=1}^{m}{\frac {w_{j}^{2}}:{d_{j}-\}}}=0.}$

이 방정식은 세속 방정식으로 알려져 있다.따라서 문제는 이 방정식의 왼쪽에서 정의한 합리적 함수의 근원을 찾는 것으로 축소되었다.

모든 일반 고유값 알고리즘은 반복적이어야 하며, 분할 및 재무 알고리즘도 다르지 않다.비선형 세속 방정식을 풀려면 뉴턴-랩슨 방법과 같은 반복적 기술이 필요하다.그러나 각 루트는 O(1) 반복에서 찾을 수 있으며, 각 루트는 $\theta {\displaystyle \mathrm{}(m}$ ${\displaystyle )}$ ${\displaystyle \Theta(m)}$플롭$$($m{\displaystyle }$ ${\displaystyle m}$ -di$$ rational function의 경우)을 필요로 하므로 이 알고리즘의 반복 부분 $\theta {\displaystyle \mathrm{}({m\mathrm{}}^{}}$ 2${\displaystyle {}^{}}$) ${\displaystylease \Theta(m^{2$

분석

알고리즘을 분할·정복하는 것이 일반적이듯이 분할·정복 반복에 대한 마스터 정리를 이용하여 실행시간을 분석한다.위에서 n${\displaystyle }n{\displaystyle }$ m /${\displaystyle 2\mathrm{}}$ ${\displaystyle n\$ 약 $m/2$}을$($를) 선택한다고 말한 것을 기억하십시오$.$ 우리는 다음과 같은 반복 관계를 작성할 수 있다.

${\displaystyle T(m)=2\time T\left({\frac {m}{2}}\오른쪽)++\테타(m^{2})}$

마스터 정리 $표기법$에서 a${\displaystyle }$= b${\displaystyle }$= ${\displaystyle 2}$ ${\displaystyle a=b=2},$ 따라서$$ ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle b{}_{}}$⁡ ${\displaystyle \mathrm{a}}$= 1 ${\displaystyle \log _{b}a=1$ 분명히 $\theta {\displaystyle \mathrm{}({}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$)${\displaystyle }$= ${\displaystyle \mathrm{\Omega }({}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$) ${\displaystyle \Teta(m^{2=})$$\Oomega (m^{1$ 그래서 우리는

$[\displaystyle T(m)=\테타(m^{2})}$

위에서 우리는 은둔자 행렬을 3각형 형태로 축소하는 데 $4{\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle {3m\mathrm{}}^{}}$ 3${\$}}}{3$}}}$플롭이$$ 필요하다는 점을 지적한 것을 기억하십시오.이는 분할 및 변환 부분의 실행 시간을 왜소하게 하며, 이 시점에서 분할 및 변환 알고리즘이 3지각 행렬에 대해 QR 알고리즘(또한 $\theta {\displaystyle \mathrm{}}$ ${\displaystyle ({}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$) ${\displaystyle \Theta (m^{2})$ 플롭을$$ 통해 제공하는 이점이 무엇인지 명확하지 않다.

분할-통화 이점은 고유 벡터도 필요할 때 발생한다.이런 경우 삼두각형 형태로의 축소는 8 ${\displaystyle {3m\mathrm{}}^{}}$ 3${\$이 걸리지만 알고리즘의 두 번째 부분 역시 $takes$(${\displaystyle {m\mathrm{}}^{}}$3 )${\displaystyle \Theta(m^{3})$가 걸린다.타당한 목표 정밀도의 QR 알고리즘의 경우${\displaystyle {this\mathrm{}}^{}}$ ${\displaystyle \mathrm{6m}}$ ${\displaystyle {}^{}}$ ${\$ 6m$^{3},$분할 및 변환의 경우${\displaystyle 4\frac{\mathrm{}}{}}$ ${\displaystyle \frac{4}{}}$ ${\displaystyle {3m\mathrm{}}^{}}$ 3 ${\$\$$약${\frac$ {$4}{3}m^{3$이러한 개선의 이유는 분할 및 변환에서 알고리즘의 $\theta {\displaystyle \mathrm{}({}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$) ${\displaystyle \Theta(m^{3})$ 부분$$(다중 $Q{\displaystyle }$ ${\displaysty Q}$ 행렬$$)은 반복과는 별개인 반면 QR에서는 모든 반복 단계에서 이러한 현상이 일어나야 하기 때문이다.8 ${\displaystyle 3m{}^{}}$ ${\$플롭을$$ 더하면 총 개선량은${\displaystyle }$9 ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$ ${\$에서 $\approx {\displaystyle }$ ${\displaystyle {4m3\mathrm{}}^{}}$ ${\$\ 약 $4m^{3}}$플롭이다$$.

분할 및 재무 알고리즘의 실용적 사용은 가장 현실적인 고유값 문제에서 알고리즘이 실제로 이것보다 더 잘 작동한다는 것을 보여주었다.그 이유는 $행렬{\displaystyle }$ Q ${\displaystyle Q}$과 벡터 $z{\displaystyle }$ ${\displaystyle$ z$}$이(가) 숫자로 희박해지는 경향이 매우 많으므로, 이는 부동소수점 정밀도보다 작은 값을 가진 항목이 많다는 것을 의미하며, 즉, 숫자 디플레이션(숫자 디플레이션)을 허용하기 때문이다.

변형 및 구현

여기에 제시된 알고리즘은 가장 간단한 버전이다.많은 실제 구현에서는 안정성을 보장하기 위해 더 복잡한 순위 1 보정이 사용된다. 일부 변형에서는 순위 2 보정을 사용하기도 한다.^{[citation needed]}

성능과 안정성 측면에서 뉴턴-래프슨 방법보다 더 잘할 수 있는 합리적인 기능에 대한 전문화된 뿌리 찾기 기법이 존재한다.이것들은 분할-금융 알고리즘의 반복적인 부분을 개선하는 데 사용될 수 있다.

분할-상호 알고리즘은 쉽게 병렬화되며, LAPACK과 같은 선형 대수 계산 패키지는 고품질 병렬 구현을 포함하고 있다.

참조

• Demmel, James W. (1997), Applied Numerical Linear Algebra, Philadelphia, PA: Society for Industrial and Applied Mathematics, ISBN 0-89871-389-7, MR 1463942.
• Cuppen, J.J.M. (1981). "A Divide and Conquer Method for the Symmetric Tridiagonal Eigenproblem". Numerische Mathematik. 36: 177–195.