디랜지먼트
Derangement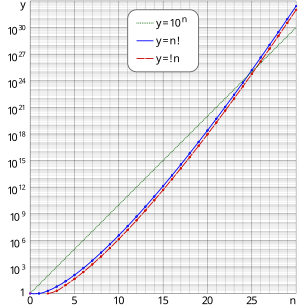
| 값표 | |||
|---|---|---|---|
| 순열, n | derangements, | ||
| 0 | 1 =1×100 | 1 =1×100 | = 1 |
| 1 | 1 =1×100 | 0 | = 0 |
| 2 | 2 =2×100 | 1 =1×100 | = 0.5 |
| 3 | 6 =6×100 | 2 =2×100 | ≈0.33333 33333 |
| 4 | 24 =2.4×101 | 9 =9×100 | = 0.375 |
| 5 | 120 =1.20×102 | 44 =4.4×101 | ≈0.36666 66667 |
| 6 | 720 =7.20×102 | 265 =2.65×102 | ≈0.36805 55556 |
| 7 | 5 040=5.04×103 | 1 854≈1.85×103 | ≈0.36785 71429 |
| 8 | 40 320≈4.03×104 | 14 833≈1.48×104 | ≈0.36788 19444 |
| 9 | 362 880≈3.63×105 | 133 496≈1.33×105 | ≈0.36787 91887 |
| 10 | 3 628 800≈3.63×106 | 1 334 961≈1.33×106 | ≈0.36787 94643 |
| 11 | 39 916 800≈3.99×107 | 14 684 570≈1.47×107 | ≈0.36787 94392 |
| 12 | 479 001 600≈4.79×108 | 176 214 841≈1.76×108 | ≈0.36787 94413 |
| 13 | 6 227 020 800≈6.23×109 | 2 290 792 932≈2.29×109 | ≈0.36787 94412 |
| 14 | 87 178 291 200≈8.72×1010 | 32 071 101 049≈3.21×1010 | ≈0.36787 94412 |
| 15 | 1 307 674 368 000≈1.31×1012 | 481 066 515 734≈4.81×1011 | ≈0.36787 94412 |
| 16 | 20 922 789 888 000≈2.09×1013 | 7 697 064 251 745≈7.70×1012 | ≈0.36787 94412 |
| 17 | 355 687 428 096 000≈3.56×1014 | 130 850 092 279 664≈1.31×1014 | ≈0.36787 94412 |
| 18 | 6 402 373 705 728 000≈6.40×1015 | 2 355 301 661 033 953≈2.36×1015 | ≈0.36787 94412 |
| 19 | 121 645 100 408 832 000≈1.22×1017 | 44 750 731 559 645 106≈4.48×1016 | ≈0.36787 94412 |
| 20 | 2 432 902 008 176 640 000≈2.43×1018 | 895 014 631 192 902 121≈8.95×1017 | ≈0.36787 94412 |
| 21 | 51 090 942 171 709 440 000≈5.11×1019 | 18 795 307 255 050 944 540≈1.88×1019 | ≈0.36787 94412 |
| 22 | 1 124 000 727 777 607 680 000≈1.12×1021 | 413 496 759 611 120 779 881≈4.13×1020 | ≈0.36787 94412 |
| 23 | 25 852 016 738 884 976 640 000≈2.59×1022 | 9 510 425 471 055 777 937 262≈9.51×1021 | ≈0.36787 94412 |
| 24 | 620 448 401 733 239 439 360 000≈6.20×1023 | 228 250 211 305 338 670 494 289≈2.28×1023 | ≈0.36787 94412 |
| 25 | 15 511 210 043 330 985 984 000 000≈1.55×1025 | 5 706 255 282 633 466 762 357 224≈5.71×1024 | ≈0.36787 94412 |
| 26 | 403 291 461 126 605 635 584 000 000≈4.03×1026 | 148 362 637 348 470 135 821 287 825≈1.48×1026 | ≈0.36787 94412 |
| 27 | 10 888 869 450 418 352 160 768 000 000≈1.09×1028 | 4 005 791 208 408 693 667 174 771 274≈4.01×1027 | ≈0.36787 94412 |
| 28 | 304 888 344 611 713 860 501 504 000 000≈3.05×1029 | 112 162 153 835 443 422 680 893 595 673≈1.12×1029 | ≈0.36787 94412 |
| 29 | 8 841 761 993 739 701 954 543 616 000 000≈8.84×1030 | 3 252 702 461 227 859 257 745 914 274 516≈3.25×1030 | ≈0.36787 94412 |
| 30 | 265 252 859 812 191 058 636 308 480 000 000≈2.65×1032 | 97 581 073 836 835 777 732 377 428 235 481≈9.76×1031 | ≈0.36787 94412 |
결합수학에서, 교란이란 집합의 원소를 순열하는 것으로, 원소가 원래 위치에 나타나지 않는 것을 말한다.즉, 변칙은 고정된 포인트가 없는 순열이다.
n 크기 집합의 변이 수를 n의 하위 요인 또는 n-th 변이 번호 또는 n-th de Montmort 숫자로 알려져 있다.일반적으로 사용되는 하위 요인에 대한 표기에는 !n, Dn, d 또는n n이 포함된다.[1][2]
하위 요인 !n은 n!/e에 가장 가까운 정수와 같으며, 여기서 n!은 n의 인자를 나타내고 e는 오일러의 수이다.[3]
난해도를 세는 문제는 1708년 피에르 레이몬드 드 몽모트에[4] 의해 처음 고려되었다; 그는 니콜라스 베르누이가 거의 동시에 그랬던 것처럼 1713년에 그것을 해결했다.
예
한 교수가 A, B, C, D 등 4명의 학생들에게 시험을 주었고, 그들이 서로의 시험 점수를 매기기를 원한다고 가정해보자.물론, 어떤 학생도 자신의 시험 성적을 매겨서는 안 된다.교수가 학생들에게 시험을 다시 돌려줄 수 있는 방법은 몇 가지인가? 즉, 학생들이 자신의 시험을 다시 받지 못하도록 할 수 있는 방법은 몇 가지인가?시험 반환을 위한 24개의 순열(4!) 중에서,
ABCD, ABC, ACBD, ACDB, ADBC, ADCB, BACD, BADC, BCAD, BCDA, BDAC, BDCA, CABD, CADB, CBAD, CBDA, CDAB, CDBA, DABC, DACB, DBAC, DBCA, DCAB, DCBA.
단지 9가지 색상이 있을 뿐이다(위의 파란색 이탤릭체로 표현된다.이 4인조 세트의 다른 모든 순열에서, 적어도 한 명의 학생은 그들 자신의 시험을 다시 받는다(대담한 빨간색으로 표시된다.
문제의 또 다른 버전은 우리가 각각 다른 사람에게 주소가 지정된 n개의 문자를 미리 주소가 지정된 봉투에 넣을 수 있는 방법의 수를 요구할 때 발생한다.
계량해석
집합의 변이도를 계산하면 모자(h ~ h라고 부름)가 n명(P1 ~ Pn)에게 돌아갈 수 있는 방법의 수를 고려하여 모자(H1 ~ Hn)가 주인에게 돌아가지 않도록 하는 해트 체크 문제에 해당된다.[5]
각 사람은 자신의 모자가 아닌 n - 1 모자 중 하나를 받을 수 있다.P가1 h를i 받는 모자에 전화를 걸어 h의i 소유자를 고려하라: P는i P의1 모자, h1 또는 다른 어떤 것을 받는다.따라서 이 문제는 가능한 두 가지 경우로 나뉜다.
- P는i h가1 아닌 다른 모자를 받는다.이 경우는 N - 1인, N - 1인 모자의 경우 P 외에1 n - 1인 모자의 경우 나머지 n - 1인 모자의 경우(Pi 이외의 P의j 경우, 상상할 수 없는 모자는 h인j 반면 P의i 경우 h인1 경우 h인 경우)가 있기 때문에 n - 1인, n - 1인 모자의 문제를 해결하는 것과 같다.이것을 볼 수 있는 또 다른 방법은 h에서1i h로 이름을 바꾸는 것이다. 여기서 derange는 더 노골적이다: 2에서 n까지의 어떤 j에 대해서도 P는j h를j 받을 수 없다.
- P는i h를1 받는다.이 경우 문제는1 P가i h의 모자를 받았고i P가1 h의 모자를 받았기 때문에 n - 2인 및 n - 2인자로 감소하여 사실상 이 두 가지 모두를 더 이상 고려하지 않게 된다.
P가1 받을 수 있는 n - 1 모자 각각에 대해, P2, …, P가n 모두 모자를 받을 수 있는 방법의 수는 두 경우에 대한 카운트의 합이다.
이것은 해트 체크 문제에 대한 해결책을 우리에게 준다: 대수학적으로 말해서, n-element 세트의 변이들의 숫자!n은
- =( n-)(! (( - )+(n - )) n\
여기서! = 1 및! 1= [6].
작은 길이의 변색 횟수는 아래 표에 제시되어 있다.
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| !n | 1 | 0 | 1 | 2 | 9 | 44 | 265 | 1,854 | 14,833 | 133,496 | 1,334,961 | 14,684,570 | 176,214,841 | 2,290,792,932 |
위에 주어진 공식과 동등한 !n에 대한 다양한 다른 표현들이 있다.여기에는 다음이 포함된다.
- 0에
그리고
- {1}{2}에 대한
여기서[ 은(는) 가장 가까운 정수 함수이고and 은(는) 바닥 함수다.[3][6]
기타 관련 공식은 다음과[7] 같다.
그리고
다음과 같은 재발도 지속된다.[6]
포함-제외원칙에 의한 파생
또한 n-set의 변이 횟수에 대한 비반복 공식도 도출할 수 있다. {\에 대해 우리는 를 k -th 객체를 고정하는 n 객체의 순열 집합으로 정의한다.이러한 집합의 i 집합의 임의 교차점은 i 객체의 특정 집합을 수정하므로(-i }순열.( ) n이(가) 있으므로 포함-제외 원칙이 산출된다.
그리고 교란이란 n개의 물체를 하나도 고치지 않는 순열이기 때문에, 이것은 암시한다.
n이 다가옴에 따른 변칙의 수 증가 ∞
보낸 사람
그리고
=- 을 대체하여 x을 즉시 얻음
이것은 무작위로 선택된 많은 수의 물체의 순열이 변질일 확률의 한계다.확률은 n이 증가함에 따라 매우 빠르게 이 한계로 수렴되며, 이것이 바로 !n이 n!/e에 가장 가까운 정수인 이유다.위의 세미로그 그래프는 변주 그래프가 순열 그래프를 거의 일정한 값으로 뒤처지게 한다는 것을 보여준다.
이 계산과 위의 한계에 대한 자세한 내용은 무작위 순열 통계에 관한 글에서 찾을 수 있다.
벨 수 측면에서 점근확대
벨 수 측면에서 변색 횟수에 대한 점증적 확장은 다음과 같다.
여기서 은(는) 고정 양의 정수이고, k 는 -th Bell 번호를 나타낸다.더욱이 큰 O기가 내포한 는 B + 1 을 초과하지 않는다[8]
일반화
프로블렘 데 렌컨트리에서는 size-n 집합의 순열 수가 정확히 k개의 고정점을 갖는지를 묻는다.
변조는 제한된 순열의 넓은 영역의 한 예다.예를 들어, 메네지 문제는 이성 커플이 남자-여자-여자-여자-여자가 앉아있는지 물어본다.테이블 주위에, 그들은 얼마나 많은 방법으로 앉을 수 있을까? 그래서 아무도 그의 또는 그녀의 파트너 옆에 앉지 않을 것인가?
More formally, given sets A and S, and some sets U and V of surjections A → S, we often wish to know the number of pairs of functions (f, g) such that f is in U and g is in V, and for all a in A, f(a) ≠ g(a); in other words, where for each f and g, there exists a derangement φ of S such that f(a) = φ(g(a)).
또 다른 일반화는 다음과 같은 문제다.
- 주어진 단어의 고정 글자가 없는 아나그램은 몇 개인가?
예를 들어, n글자 A와 m글자 B와 같이 두 개의 다른 문자로만 이루어진 단어의 경우, 대답은 물론 n = m인지 여부에 따라 1이나 0으로 되어 있는데, 고정된 문자 없이 아그램이 형성되는 유일한 방법은 모든 A를 B와 교환하는 것인데, 이는 n = m일 경우에만 가능하다.일반적인 경우, 문자 X1, 문자22 X, 문자r X가1r n인 단어의 경우, (포함 제외 공식을 적절히 사용한 후) 답이 다음과 같은 형식을 갖는 것으로 나타난다.
다항식 P의n 특정 시퀀스에 대해, 여기서 P는n n도를 가진다.그러나 사례 r = 2에 대한 위의 답변은 직교 관계를 제공하며, P가n 라구에르 다항식(쉽게 결정되는 부호까지)인 경우다.[9]
특히 고전적인 진부함을 위해서.
계산 복잡성
주어진 순열 그룹(순열 그룹을 생성하는 주어진 순열 집합으로 설명됨)에 어떤 변칙이 있는지 여부를 결정하는 것은 NP-완전이다.[10]
참조
- ^ "하위 요소"라는 이름은 윌리엄 앨런 휘트워스에서 유래되었다. 참조Cajori, Florian (2011), A History of Mathematical Notations: Two Volumes in One, Cosimo, Inc., p. 77, ISBN 9781616405717.
- ^ Ronald L. Graham, Donald E. Knuth, 오렌 파타슈닉, 콘크리트 수학 (1994), 애디슨-웨슬리, 리딩 MA. ISBN 0-201-55802-5
- ^ a b Hassani, M. "변칙과 응용" J. 정수 Seq. 6, 03.1.2, 1–8, 2003
- ^ 드 몽모트, P. R. (1708)에세이 단날리스 수르 레즈 턱스 드 해저드파리: 자크 퀼라우.Seconde Edition, Revue & aguentée de Plusieurs Letres.파리: 자크 퀼라우, 1713년
- ^ Scoville, Richard (1966). "The Hat-Check Problem". American Mathematical Monthly. 73 (3): 262–265. doi:10.2307/2315337. JSTOR 2315337.
- ^ a b c Stanley, Richard (2012). Enumerative Combinatorics, volume 1 (2 ed.). Cambridge University Press. Example 2.2.1. ISBN 978-1-107-60262-5.
- ^ Weisstein, Eric W. "Subfactorial". MathWorld.
- ^ Hassani, M. "통합에 의한 순열과 교번 합" J. 정수 Seq. 23, 20.7.8조, 1–9조, 2020
- ^ Even, S.; J. Gillis (1976). "Derangements and Laguerre polynomials". Mathematical Proceedings of the Cambridge Philosophical Society. 79 (1): 135–143. doi:10.1017/S0305004100052154. Retrieved 27 December 2011.
- ^ Lubiw, 안나(1981년),"어떤 NP-완전 문제 그래프 isomorphism과 비슷한", SIAM 저널 컴퓨팅에, 10(1):11–21, doi:10.1137/0210002, MR0605600.Babai, 라슬로(1995년),"자기 동형 사상 단체, 유질 동상, 재건", 핸드 북 조합론, Vol1,2(PDF), 암스테르담:.Elsevier,를 대신하여 서명함. 1447–1540, MR1373683, 안나 Lubiw는 다음 문제는 NP-완전을 주장하고 놀랄 만한 결과:.주어진 치환 군?fixed-point-free 요소를 갖고 있나.
외부 링크
| 무료 사전인 Wiktionary에서 이상한 점을 찾아 보십시오. |
- Baez, John (2003). "Let's get deranged!" (PDF).
- Bogart, Kenneth P.; Doyle, Peter G. (1985). "Non-sexist solution of the ménage problem".
- Dickau, Robert M. "Derangement diagrams". Mathematical Figures Using Mathematica.
- Hassani, Mehdi. "Derangements and Applications". Journal of Integer Sequences (JIS), Volume 6, Issue 1, Article 03.1.2, 2003.
- Weisstein, Eric W. "Derangement". MathWorld–A Wolfram Web Resource.








![{\displaystyle !n=\left[{\frac {n!}{e}}\right]=\left\lfloor {\frac {n!}{e}}+{\frac {1}{2}}\right\rfloor }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d522701b28d640964b2e50f781b9e10c385898f5) 대한
대한 ![{\displaystyle \left[x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bee30b48da3d61e9dfa898ca4d209afdcc6503dc)
 (는)
(는) 







 (가) 있으므로
(가) 있으므로 





 (는) 고정 양의 정수이고,
(는) 고정 양의 정수이고, 







