실린더 응력

역학에서 실린더 응력은 회전 대칭이 있는 응력 분포로, 즉 응력된 물체가 어떤 고정 축을 중심으로 회전해도 변하지 않는다.

실린더 응력 패턴은 다음을 포함한다.

• 원주 응력 또는 후프 응력, 접선(azimuth) 방향의 정상 응력.
• 원통형 대칭 축에 평행한 일반적인 응력인 축 응력
• 방사상 응력, 대칭축에 수직이지만 동일 평면 방향에서의 정상 응력.

이 세 가지 주요 응력-후프, 세로 및 방사형 응력은 상호 수직 3축 응력 시스템을 사용하여 분석적으로 계산할 수 있다.^[1]

후프 스트레스의 고전적인 예(그리고 이름 붙임)는 나무 통의 쇠줄, 즉 후프에 가해지는 장력이다. 닫힌 직선 파이프에서 압력 차이에 의해 원통형 파이프 벽에 가해지는 어떤 힘도 궁극적으로 후프 응력을 발생시킬 것이다. 마찬가지로, 이 배관이 평평한 끝 마개를 가진 경우, 정압에 의해 그것들에 가해지는 힘은 동일한 배관 벽에서 수직 축 응력을 유도할 것이다. 얇은 섹션은 종종 무시할 수 없을 정도로 작은 방사상 응력을 가지지만, 더 두꺼운 원통형 쉘의 정확한 모델은 그러한 응력을 고려해야 한다.

두꺼운 벽 압력용기에서는 유리한 초기 응력 패턴을 허용하는 시공 기법을 활용할 수 있다. 내부 표면의 이러한 압축 응력은 가압 실린더의 전체적인 후프 응력을 감소시킨다. 이러한 성격의 원통형 용기는 일반적으로 서로 수축(또는 확장)되는 동심원통(즉, 내장 수축-핏 실린더)으로 구성되지만 두꺼운 실린더의 자동 회수에도 불구하고 단수 실린더로 수행될 수 있다.^[2]

정의들

후프 응력

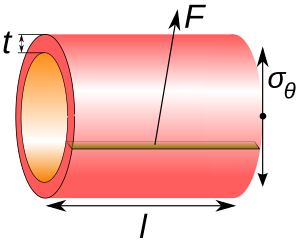
후프 응력은 실린더 벽의 모든 입자에 대해 양방향으로 원주적으로 작용하는 영역(물체의 축과 반지름에 수직)에 대한 힘이다. 그것은 다음과 같이 설명할 수 있다.

${\displaystyle \sigma _{\teta }={\dfrac {F}{tl}\}}$

여기서:

• F는 다음과 같은 두 개의 길이를 측면으로 하는 실린더 벽 면적에 원주적으로 가해지는 힘이다.
• t는 실린더의 방사형 두께다.
• l는 실린더의 축 길이이다.

원주응력을 설명할 때 후프 응력의 대안으로 벽 응력 또는 벽 장력(T)이 있는데, 이는 보통 전체 방사상 두께를 따라 가해지는 총 원주력으로 정의된다.^[3]

${\displaystyle T={\dfrac {F}{l}\ }$

원주응력은 축응력 및 방사응력과 함께 원통형 좌표에서 응력텐서의 구성요소다.

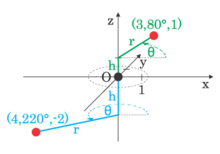
회전 대칭이 있는 물체에 가해지는 힘을 원통형 좌표 r, z, θ에 평행한 성분으로 분해하는 것이 보통 유용하다. 이러한 힘의 구성 요소는 각각 반지름 응력, 축 응력, 후프 응력 등 해당 응력을 유도한다.

내부 압력과 관계

박벽 가정

박벽 가정이 유효하려면 선박의 벽 두께가 반지름의 약 10분의 1(흔히 지름/t > 20으로 언급됨) 이하가 되어야 한다.^[4] 이를 통해 벽을 표면으로 처리하고 이후 얇은 벽 원통형 압력 용기의 내부 압력에 의해 발생하는 후프 응력을 추정하기 위해 Young-Laplace 방정식을 사용할 수 있다.

${\displaystyle {\sigma }_{}}$= ${\displaystyle P{\displaystyle \frac{}{}}}$ ${\displaystyle {\displaystyle \frac{r}{}}}$ ${\displaystyle {\displaystyle \frac{}{}}}$ $displaystyle \sigma _{\ta }={\dfrac {Pr}{t}\}($원통형)

${\displaystyle {\sigma }_{}}$= ${\displaystyle P{\displaystyle \frac{}{}}}$ ${\displaystyle {\displaystyle \frac{r}{}}}$ ${\displaystyle {\displaystyle \frac{\mathrm{}}{}}}$ ${\displaystyle {\displaystyle \frac{t}{}}}$ $displaystyle \sigma _{\ta }={\dfrac {Pr}{2t}\}($구)$$

어디에,

• P는 내부 압력이다.
• t는 벽두께다
• r은 실린더의 평균 반지름이다.
• ${\displaystyle {\sigma }_{}}$ $displaystyle \sigma _{\theta }\\!}$는 후프 응력이다.

얇은 껍질에 대한 후프 응력 방정식은 내부 터고 압력이 여러 대기에 도달할 수 있는 식물 세포와 박테리아를 포함한 구형 혈관에도 근사적으로 유효하다. 실린더(파이프 및 튜브)에 대한 실용적인 엔지니어링 적용에서 후프 응력은 종종 압력을 위해 다시 배열되며, 이를 Barlow의 공식이라고 한다.

P용 인치-파운드-초계통(IPS) 단위는 평방인치당 파운드-힘(psi)이다. t와 d의 단위는 인치(in)이다. P의 SI 단위는 파스칼(Pa)이고, t와 d=2r는 미터(m)이다.

용기의 끝이 닫혔을 때, 내부 압력이 실린더의 축을 따라 힘을 발생시키기 위해 그들에게 작용한다. 이것은 축응력이라고 알려져 있으며 보통 후프 응력보다 적다.

${\displaystyle \sigma _{z}={\dfrac {F}{A}}}={\dfrac {Pd^{2}}{{(d+2t)^{2}-d^{2}}\}}$

이 값은 대략 다음과 같을 수도 있다.

${\displaystyle \sigma _{z}={\dfrac {Pr}{2t}\}$

또한 표면에 수직으로 개발되어 얇은 벽이 있는 실린더에서 다음과 같이 추정할 수 있는$$ 방사상 응력 $\sigma {\displaystyle {}_{}}$ ${\displaystyle r_{}}$ $displaystyle \sigma _{r}\}$도 있다.

${\displaystyle \sigma _{r}={-P}\ }$

단, 박벽 가정에서는 $r{\displaystyle {\displaystyle \frac{}{}}}$ ${\displaystyle {\displaystyle \frac{t}{}}}$ $displaystyle${\$dfrac {r}{t}\}}$이(가) 크기 때문에 대부분의 경우 이 구성요소는 후프 및 축 응력에 비해 무시해도 되는 것으로 간주된다. ^[5]

두꺼운 벽의 용기

언제가 실린더에 연구되어야 하는 r이 나의 u d/thic가 ness{\displaystyle radius/thickness}비율의 10(자주 d로 바삭바삭한 meter/th를 인용했다 나는 c가 ness<>20{\displaystyle diameter/thickness<, 20})은 세벽 실린더 방정식은 더 이상한 이후 스트레스 다양하게 사이에 내부. outside 단면을 통한 표면 및 전단 응력을 더 이상 무시할 수 없다.

이러한 스트레스와 변종은 프랑스 수학자 가브리엘 라메에 의해 개발된 일련의 방정식인 라메 방정식을 사용하여 계산할 수 있다.

${\displaystyle \sigma _{r}=A-{\dfrac {B}{r^{2}}\}}}$

${\displaystyle \sigma _{\theta }=A+{\dfrac {B}{r^{2}}\}}}$

여기서:

${\displaystyle A}${\$displaystyle A}$ 및$$ B ${\displaystyle B}$은(는) 통합 상수로, 경계 조건에서 찾을 수 있다.

${\displaystyle r}$ ${\displaystyle r}$은(예: 내부 또는 외부 벽) 관심 지점의 반지름이다.

$경계$ 조건의 검사를 통해$$a [\displaystayle$$ A$},$ $B$ ${\displaystyle B}.$ 예를 들어, 가장 간단한 경우는 고체 실린더:

${\displaystyle {Ri}_{}}$= ${\displaystyle 0}$ ${\displaystyle R_{i}=0}$이면 ${\displaystyle \mathrm{B<img\; alt="\{\backslash displaystyle\; R\_\{i\}=0\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/87d92cf3158cdc682c0e2a32b891151f1d832914"\; style="vertical-align:\; -0.671ex;\; width:6.825ex;\; height:2.509ex;"\; papago-attr-id="79">}}$= 0 ${\displaystyle B=0}$이고 고체$$ 실린더는 내부 압력을 가질 수 없으므로 $A{\displaystyle }$= ${\displaystyle {}_{}}$ ${\displaystyle o_{}}$ ${\$

Being that for thick-walled cylinders, the ratio ${\displaystyle {\dfrac {r}{t}}\ }$ is less than 10, the radial stress, in proportion to the other stresses, becomes non-negligible (i.e. P is no longer much, much less than Pr/t and Pr/2t), and so the thickness of the wall becomes a major consideration for design (Harvey, 1974, pp. 57).

압력 용기 이론에서, 벽의 주어진 요소는 3축 응력 시스템으로 평가되며, 세 가지 주요 응력은 후프, 세로, 반지름이다. 따라서 정의에 따르면 가로, 접선 또는 방사상 평면에 전단 응력이 존재하지 않는다.^[6]

두꺼운 벽의 실린더에서, 어느 지점에서나 최대 전단 응력은 최대 응력과 최소 응력 사이의 대수적 차이의 절반으로 주어지며, 따라서 후프와 방사형 응력 사이의 차이의 절반과 같다. 내부 표면에서 피복 응력은 최대치에 도달하는데, 이는 두꺼운 실린더의 실제 파열 시험과 잘 상관되기 때문에 실패의 기준이 되기 때문에 중요하다(Harvey, 1974, 페이지 57).

실용효과

공학

골절은 주응력이 가장 크기 때문에 다른 외부 부하가 없을 때 후프 응력에 의해 제어된다. 후프는 내부에서 가장 큰 응력을 경험하므로(외부와 내부는 동일한 총 변형률을 경험하며, 이는 서로 다른 원주에 걸쳐 분포한다) 파이프 내부로부터 파이프 균열이 이론적으로 시작되어야 한다. 지진 후 배관 점검에는 보통 배관 내부에 카메라를 넣어 균열 여부를 점검하는 작업이 수반되는 이유다. 항복은 후프 응력과 부재 시 세로 또는 반지름 응력을 포함하는 등가 응력에 의해 제어된다.

약

혈관벽이나 위장벽의 병리학에서 벽긴장은 혈관벽의 근육긴장을 나타낸다. 라플라스 법칙의 결과 혈관벽에 동맥류가 형성되면 혈관 반경이 높아졌다. 이는 혈관의 내부 힘이 감소하고 따라서 동맥류가 파열될 때까지 계속 확장된다는 것을 의미한다. 비슷한 논리가 내장에 게실리 형성에 적용된다.^[7]

그 이론의 역사적 전개

실린더의 스트레스에 대한 최초의 이론적 분석은 19세기 중반의 엔지니어 윌리엄 페어베언에 의해 그의 수학 분석가 이튼 호지킨슨의 도움을 받아 개발되었다. 그들의 첫 번째 관심은 증기 보일러의 설계와 고장을 연구하는 것이었다.^[9] 페어베언은 후프 응력이 종방향 응력의 두 배라는 것을 깨달았는데, 이는 리벳팅으로 결합된 압연 시트에서 보일러 껍질 조립에 중요한 요소였다. 이후 작업은 교량 건설과 박스 거더의 발명에 적용되었다. 체스토 철교에서는 주철 기둥이 외부 연철 띠에 의해 강화된다. 수직, 종방향 힘은 압축력인데, 주철은 잘 저항할 수 있다. 후프 응력은 인장력이므로 주철보다 인장강도가 우수한 재료인 연철도 첨가된다.

참고 항목

• 실린더 응력에 의해 발생할 수 있음:
  • 보스턴 몰러시스 재난
  • 보일러 폭발
  • 비등액 팽창 증기폭발
• 관련 엔지니어링 주제:
  • 응력집중
  • 정수시험
  • 버클링
  • 혈압#관계_to_wall_tension
  • 배관#스트레스_분석
• 이 스트레스의 영향을 많이 받는 설계:
  • 압력 용기
    • 로켓엔진
  • 플라이휠
  • 플로렌스 대성당의 돔

참조

• Thin-walled Pressure Vessels. Engineering Fundamentals. 19 June 2008.

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "실린더 스트레스" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2012년 3월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)