절삭재고문제

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "주식 절단 문제" – 뉴스 · 신문 · 도서 · 학자 · JSTOR (2015년 4월) (이 템플릿 메시지 제거 방법과 시기 확인)

운영연구에서 절삭재료는 종이롤이나 판금 등 표준 크기의 표준재료를 지정된 크기의 조각으로 자르면서도 낭비되는 재료는 최소화하는 문제가 있다. 그것은 수학의 최적화 문제로서 산업에서의 응용에서 발생한다. 계산 복잡성 측면에서 문제는 배낭 문제로 환원할 수 있는 NP-하드 문제다. 이 문제는 정수 선형 프로그래밍 문제로 공식화될 수 있다.

1차원 절삭기 문제 그림

종이 기계는 각각 폭이 5600mm인 마스터(점보) 롤을 무제한으로 생산할 수 있다. 아래 표에서 다음 13개 항목을 잘라야 한다.

이런 종류의 문제에 있어서 중요한 것은 같은 마스터롤로부터 많은 다른 제품 단위를 만들 수 있다는 것이며, 가능한 조합의 수는 그 자체로 매우 크고, 일반적으로 열거하기에 사소한 것이 아니라는 것이다.

따라서 문제는 수요가 충족되고 낭비가 최소화되도록 마스터롤에서 최적의 제품 롤링 패턴 세트를 찾는 것이다.

폭	# 항목
1380	22
1520	25
1560	12
1710	14
1820	18
1880	18
1930	20
2000	10
2050	12
2100	14
2140	16
2150	18
2200	20

경계 및 검사

제품 총량을 각 마스터 롤의 크기로 나누어 단순 하한을 구한다. 필요한 총 제품은 1380 x 22 + 1520 x 25 + ... + 2200 x 20 = 407160 mm. 각 마스터롤은 5600mm로 최소 72.7롤이 필요하며, 이는 73롤 이상이 필요하다는 것을 의미한다.

해결책

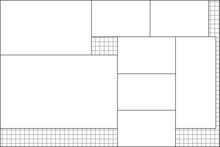
이 작은 경우에 가능한 308개의 패턴이 있다. 최적의 답은 73개의 마스터롤이 필요하며 0.401%의 폐기물을 가지고 있다. 이 경우 이 수준의 폐기물을 가진 최소 패턴 수는 10개임을 계산적으로 보여줄 수 있다. 또한 각각 10개의 패턴과 0.401%의 낭비를 가진 19개의 다른 솔루션이 존재한다고 계산할 수 있으며, 그 중 하나는 아래 그림과 같이 표시된다.

반복	내용물
2	1820 + 1820 + 1820
3	1380 + 2150 + 1930
12	1380 + 2150 + 2050
7	1380 + 2100 + 2100
12	2200 + 1820 + 1560
8	2200 + 1520 + 1880
1	1520 + 1930 + 2150
16	1520 + 1930 + 2140
10	1710 + 2000 + 1880
2	1710 + 1710 + 2150
73

분류

재고 절삭 문제는 여러 가지 방법으로 분류할 수 있다.^[1] 한 가지 방법은 절삭의 치수성이다. 위의 예는 1차원(1D) 문제를 보여준다. 다른 1D 산업 적용은 파이프, 케이블 및 강철봉을 절단할 때 발생한다. 가구, 의류, 유리 생산 등에서 2차원(2D) 문제가 발생한다. 주종목이나 필요한 부품이 불규칙한 형태일 때(피혁, 섬유, 금속 산업에서 흔히 마주치는 상황) 이것을 보금자리 문제라고 한다.

절단을 수반하는 3차원(3D) 애플리케이션은 많이 알려져 있지 않지만, 밀접하게 연관된 3D 패킹 문제는 운송 용기에 물체를 포장하는 것과 같은 산업적 애플리케이션(예: 컨테이너화: 관련 구면 패킹 문제는 17세기(케플러 추측)부터 연구되어 왔다.

적용들

생산량이 많은 경우, 특히 기본 자재가 더 작은 단위로 더 잘려진 큰 롤로 생산될 때 산업적 적용이 발생한다(롤 슬레이팅 참조). 이것은 종이와 플라스틱 필름 산업에서뿐만 아니라 강철이나 황동과 같은 평평한 금속의 생산에서도 이루어진다. 기계 및 공정 한계, 고객 요구사항 및 품질 문제로 인한 특별한 생산 제약으로 인해 발생하는 많은 변형과 추가 제약조건이 있다. 몇 가지 예는 다음과 같다.

• 2단계, 1단계에서 생산되는 롤이 두 번째로 처리된다. 예를 들어, 모든 사무실 문구류(예: 유럽의 A4 크기, 미국의 Letter 크기)는 그러한 과정에서 생산된다. 2단계의 기계가 1단보다 좁기 때문에 합병증이 발생한다. 두 생산단계의 효율적 활용은 (에너지 또는 재료 사용의 관점에서) 중요하며, 1차 단계에 효율적인 것은 2차 단계에 비효율적일 수 있어 절충으로 이어질 수 있다. 야금 처리된 필름(간식 포장에 사용)과 종이에 부착된 플라스틱 압출(액체 포장, 예를 들어 주스 상자 등)은 그러한 과정의 또 다른 예다.
• 슬팅 프로세스가 물리적 또는 논리적 구속조건을 갖는 윈더 구속조건: 매우 일반적인 구속조건은 특정 수의 슬팅 나이프만 사용할 수 있으므로 실현 가능한 패턴이 최대 개수의 롤을 포함해서는 안 된다는 것이다. 윈더기계는 표준화되어 있지 않기 때문에 다른 제약조건들이 매우 많이 부딪힌다.
• 고객 요구사항의 예로는 두 개의 가장자리 위치 중 하나에서 특정 주문을 충족할 수 없는 경우가 있다. 이는 시트의 가장자리는 두께의 차이가 더 큰 경향이 있고 일부 적용은 이에 매우 민감할 수 있기 때문이다.
• 품질 문제의 예로는 마스터 롤에 절단해야 하는 결함이 포함되어 있는 경우를 들 수 있다. 사진용지나 타이벡과 같은 까다로운 품질 특성을 가진 값비싼 재료는 낭비되는 면적을 최소화하도록 조심스럽게 최적화되어야 한다.
• 다중 기계 문제는 둘 이상의 기계에서 주문이 생산될 수 있고 이 기계들의 폭이 다를 때 발생한다. 일반적으로 둘 이상의 마스터 롤 너비를 사용할 수 있으면 낭비가 상당히 개선된다. 그러나 실제로는 추가적인 순서 분할 제약 조건을 고려해야 할 수 있다.
• 생산한 롤이 지름이 같을 필요는 없지만 범위 내에서 달라질 수 있는 반연속적인 문제도 있다. 이것은 일반적으로 시트 오더와 함께 발생한다. 이것은 때때로 1차원 문제로 알려져 있다. 이 변형은 골판지의 생산에서도 발생하는데, 여기서 골판지 스케줄링 문제를 다소 혼란스럽게 부른다.
• 일부 종이 기계는 요구 품목에 비해 상대적으로 협소하기 때문에, 일부 기업은 스키빙(웹용접이라고도 함) 2차 공정에 투자했는데, 여기서 두 개의 리엘(초기 점보 릴을 잘라 생산)이 나란히 결합(중첩이 약간 있음)되어 더 넓은 롤을 구성한다. 1차 공정에서 더 좁은 릴을 생산하면 전체 폐기물이 감소한다.^[2]
• 금속 산업에서 한 가지 중요한 차이점은 일반적으로 마스터 롤이 더 일찍 생산되고 일반적으로 서로 다르다는 것이다(폭과 길이 면에서 모두). 따라서 위에서 언급한 다중 기계 문제와 유사성이 있다. 폐기물은 가로 방향과 세로 방향으로 모두 발생할 수 있기 때문에 길이 편차가 존재하면 2-D 문제가 발생한다.^{[citation needed]}
• 단두대 문제는 시트를 지정된 크기의 직사각형으로 자르는 또 다른 2-D 문제지만, 각 시트에 걸쳐 계속되는 절단만 허용된다. 이 문제의 산업적 적용은 유리 산업에서 찾을 수 있다.

• 1차원 사례의 경우 주어진 수요를 충족시킬 최적의 마스터 크기를 결정하는 절삭 재고 문제는 어소트먼트 문제로 알려져 있다.^[3]

역사

절삭 주식 문제는 1939년 칸토로비치에 의해 처음 공식화되었다.^[4] 컴퓨터가 널리 보급되기 전인 1951년에 L. V. 칸토로비치와 V. A. 잘갈러는 선형 프로그래밍의 도움을 받아 절단 단계에서 재료의 경제적인 사용 문제를 해결할 것을 제안했다^[5]. 제안된 기법은 후에 칼럼 생성법이라고 불렸다.

수학적 공식화 및 솔루션 접근 방식

절삭대금 문제에 대한 표준 공식은 각각 ${\displaystyle q_{}}$ j ${\$ 조각이$$ 필요한 m 오더 목록으로 시작한다$.$ $여기$서${\displaystyle }$j = ${\displaystyle 1}$ ${\displaystyle \dots ,}$ ${\displaystyle m}$ ${\displaysty j=1,\ldots,m}.$ 그런 다음 가능한 모든 절삭 조합의 목록을 작성한다(흔히 "패턴" 또는 "구성"이라고 함). $C{\displaystyle }$ ${\displaystyle C}$을(를) 이러한 패턴의 개수로 설정하십시오$$. $우리$는 각 패턴에 양수 변수 ${\displaystyle x_{}}$ i ${\$를 몇 번 사용해야 하는지 나타내는$$양의 정수 변수 x ${\displaystyle i}$을(를) 연결한다${\displaystyle .}$ 여기서 $i{\displaystyle }$ = ${\displaystyle 1}$,${\displaystyle \dots ,}$ ${\displaystyle C}$ ${\displaystyle i=1,\ldots,$ C$\}.$ 선형 정수 프로그램은 다음과 같다.

${\displaystyle \min \sum _{i=1}^{C}c_{i}x_{i}}}}}$

${\displaystyle {\text{s.t.}}}\sum _{i=1}^{C}a_{ij}x_{i}\geq_{j}}\quad \quad \quad \forall j=1,\dots,m}$

${\displaystyle x_{}}$ ${\displaystyle i_{}}$≥ ${\displaystyle 0}$ ${\displaystyle x_{i}\geq$ 0$\},$ 정수

여기서 ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\$는 패턴 $i{\displaystyle }$ ${\displaystyle i}$에 $j{\displaystyle }$ ${\displaystyle j}$이(가) 나타나는$$ 횟수고$$$$ ${\displaystyle c_{}}$ ${\$는 패턴 $i{\displaystyle }$ ${\displaysty$ i$}$의 비용(폐기물)이다$.$ 수량 제약의 정확한 성질은 미묘하게 다른 수학적 특성으로 이어질 수 있다. 위의 공식의 수량 제약조건은 최소 제약조건이다(최소한 각 주문의 주어진 양을 생산해야 하지만, 아마도 더 많이 생산되어야 한다).

$c{\displaystyle {}_{}}$ ${\displaystyle i_{}}$= ${\displaystyle 1}$ ${\displaystyle c_{i}=1$ 목적상 활용된 마스터 항목의 수를 최소화하고, 생산되는 수량에 대한 제약이 균등으로 대체되면 빈 패킹 문제라고 한다.

가장 일반적인 공식은 양면 제약조건을 가지고 있다(그리고 이 경우 최소 폐기물 용액은 최소 마스터 항목 수보다 더 많이 소비할 수 있다).

${\displaystyle q_{j}\leq \sum _{n}a_{ij}x_{i}\leq Q_{j}\quad \quad \forall j=1,\dots ,m}$

이 공식은 1차원적인 문제에만 적용되는 것이 아니다. 폐기물 최소화가 목적이 아니라 생산된 품목의 총가치를 극대화하여 각 주문이 다른 가치를 가질 수 있도록 하는 것을 포함하여 많은 변형이 가능하다.

일반적으로 가능한 패턴의 수는 주문수인 m의 함수로 기하급수적으로 증가한다. 따라서 주문 수가 증가함에 따라 가능한 절단 패턴을 열거하는 것이 비실용적이 될 수 있다.

대안적 접근법은 지연된 칼럼 생성 방식을 사용한다. 이 방법은 단지 몇 가지 패턴으로 시작함으로써 재고 문제를 해결한다. 그것은 필요할 때 추가 패턴을 생성한다. 1차원 사례의 경우 선형 프로그램의 이중 변수 정보를 이용하여 배낭 문제라는 보조 최적화 문제를 해결함으로써 새로운 패턴이 도입된다. 배낭 문제는 분기와 바운드, 동적 프로그래밍 등 해결 방법이 잘 알려져 있다. 지연 기둥 생성 방법은 특히 문제의 크기가 커짐에 따라 원래의 접근 방식보다 훨씬 더 효율적일 수 있다. 절삭주 문제에 적용되는 칼럼 세대 접근법은 길모어와 고모리가 1960년대에 발표한 연재 논문에서 개척한 것이다.^[6][7] 길모어와 고모리는 이러한 접근방식이 (굴절) 최적의 솔루션으로 수렴할 수 있도록 보장되어 있으며, 사전에 가능한 패턴을 모두 열거할 필요가 없다는 것을 보여주었다.

원래의 길모어와 고모리 방법의 한계는 통합성을 취급하지 않기 때문에 용액에 분수가 포함될 수 있다는 것이다. 예를 들어 특정 패턴을 3.67회 생성해야 한다. 가장 가까운 정수로 반올림하면 차선의 해결책 및/또는 일부 주문의 과소 또는 과잉 생산(그리고 양면 수요 제약이 있는 경우 실현 불가능)으로 이어질 수 있다는 점에서 효과가 없는 경우가 많다. 이러한 제한은 현대 알고리즘에서 극복되는데, 이 알고리즘은 매우 큰 문제 사례(일반적으로 실제보다^[8][9] 더 큰 문제)를 최적성으로 해결할 수 있다.

재고 절삭 문제는 동일한 양의 폐기물을 가진 복수 솔루션이 가능하다는 점에서 종종 매우 퇴보적이다. 이러한 퇴행성은 폐기물의 양에 영향을 주지 않고 새로운 패턴을 만들어내면서 물건을 옮길 수 있기 때문에 발생한다. 이는 다음과 같은 일부 다른 기준과 관련된 전체 관련 문제를 야기한다.

• 최소 패턴 개수 문제: 최소 폐기 솔루션 중에서 최소 패턴 개수 솔루션을 찾는 방법. 이것은 낭비가 알려졌을 때에도 매우 어려운 문제다.^[10][11][12] 크기가 n인 균등 구속적 1차원 인스턴스(instance)는 모두 n + 1 패턴 이하의 최소 1개의 폐기물 용액을 가지고 있다는 추측이 있다. 이런 추측이 처음 반박된 것은 2020년 4월, 11개의 패턴을 필요로 하는 9개의 크기를 가진 예다.^[13]
• 최소 스택 문제: 이는 패턴의 시퀀싱과 관련이 있어 언제든지 부분적으로 완료된 주문이 너무 많아서는 안 된다. 이것은 동적 프로그래밍에 기반한 효율적인 알고리즘이 발표된 2007년까지 개방된 문제였다.^[14]
• 칼의최소개수는(1차원 문제의 경우):이는 슬래팅 칼이 이동해야 하는 횟수를 최소화하기 위해 패턴을 염기서열화하고 허용하는 것과 관련이 있다. 이것은 일반적인 여행 판매원 문제의 특별한 경우다.

참고 항목

• 고다중성 빈 패킹
• 구성 선형 프로그램

참조

추가 읽기

• Chvátal, V. (1983). Linear Programming. W.H. Freeman. ISBN 978-0-7167-1587-0.
• 하템 벤 아모르, J.M. 발레리오 데 카르발호, 칼럼 생성의 절삭 재고 문제, 가이 디폴리에스, 자크 데스로시어즈, 마리우스 M이 편집했다. 솔로몬, 스프링거, 2005, 16세, ISBN 0-387-25485-4
• M. Delorme, M. 이오리, S. 마르텔로, 빈 포장 및 절삭 재고 문제: 수학적 모델 및 정확한 알고리즘, 유럽 운영 연구 저널 2016, 255, 1–20, doi:10.1016/j.ejor.2016.04.030