콕시터 콤플렉스

이 글에는 참고문헌, 관련 독서 또는 외부 링크 목록이 수록되어 있으나 인라인 인용구가 부족하여 출처가 불분명하다. 좀 더 정밀한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오.(2021년 5월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

수학에서 H. S. M. Coxeter의 이름을 딴 Coxeter 콤플렉스는 Coxeter 그룹과 연관된 기하학적 구조(간단한 콤플렉스)이다.콕시터 단지는 건물을 지을 수 있는 기본적인 물체로서 건물의 아파트를 형성한다.

건설

표준 선형 표현

Coxeter 시스템$({\displaystyle W}$, S${\displaystyle }$) ${\displaystyle(W,S)}$과(와) 연관된 Coxeter 복합체 건설의 첫 번째 성분은 $W{\displaystyle }$ ${\displaystyle W}$의 정식 표현이라 불리는$$W ${\displaystyle W}$의 특정 표현이다$.$

Let ${\displaystyle (W,S)}$ be a Coxeter system with Coxeter matrix ${\displaystyle M=(m(s,t))_{s,t\in S}}$. The canonical representation is given by a vector space ${\displaystyle V}$ with basis of formal symbols ${\displaystyle (e_{s})_{s\in S}}$, which isequipped with the symmetric bilinear form ${\displaystyle B(e_{s},e_{t})=-\cos \left({\frac {\pi }{m(s,t)}}\right)}$. In particular, ${\displaystyle B(e_{s},e_{s})=1}$. The action of ${\displaystyle W}$ on ${\displaystyle V}$ is then$s{\displaystyle }$(${\displaystyle v}$ ${\displaystyle )}$= v${\displaystyle }$- ${\displaystyle 2}$ ${\displaystyle \mathrm{B}}$( ${\displaystyle e}$ ${\displaystyle s_{}}$ v${\displaystyle }$) ${\displaystyle {}_{}}$ ${\displaystyle s_{}}$ ${\$로 주어진다$.$

이 표현은 Coxeter 그룹 이론에 몇 가지 기초적 특성을 가지고 있다. 예를 들어, $B{\displaystyle }$ ${\displaystyle B}$은 $W{\displaystyle }$ ${\displaystyle W}$이 유한한 경우에만 양적으로 명확한 것이다$$.$W{\displaystyle }$ ${\displaystyle W}$의 충실한 표현이다$.$

챔버스와 티츠콘

이 표현은 $W{\displaystyle }$ ${\displaystyle W}$을(를) 반사 그룹으로 설명하며, $B{\displaystyle }$ ${\displaystyle B}$이(가) 양적으로 확실하지 않을 수 있다는$$ 점을 유의한다.It becomes important then to distinguish the representation ${\displaystyle V}$ from its dual ${\displaystyle V^{*}}$. The vectors ${\displaystyle e_{s}}$ lie in ${\displaystyle V}$ and have corresponding dual vectors ${\displaystyle e_{s}^{\vee }}$ in ${\displaystyle V^{*}$$}$이(가) 제공

${\displaystyle \langle e_{s}^{\vee },v\rangele =2B(e_{s}v),}$

여기서 각이 있는 $괄호$는 V ${\displaystyle {\ast }^{}}$ ${\$와 V ${\displaystyle V}$ 사이의 자연스러운 쌍을 나타낸다$.$

이제 $W{\displaystyle }$ ${\displaystyle W}$이(가) $V{\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$ ${\$에 대해$$ 동작하고$$ 동작은 다음에 의해 주어진다.

${\displaystyle s(f)=f-\langle f,e_{s}\rangele e_{s}^{\vee }}}$

for ${\displaystyle s\in S}$ and any ${\displaystyle f\in V^{*}}$. Then ${\displaystyle s}$ is a reflection in the hyperplane ${\displaystyle H_{s}=\{f\in V^{*}:\langle f,e_{s}\rangle =0\}}$. One has the fundamental chamber > 0 S} $displaystyle {\mathcal${\$c}=\{f\in$ V$^{*}:\langle f, e_{s}\rangele >0\\\ forall$s\$s$ 이것은 소위 $벽$인 ${\displaystyle H_{}}$ {\$displaystystyle H_{s}$에 면한다$.$${\displaystyle \mathrm{다른}}$ 챔버는 변환을 통해$$ ${\displaystyle C\mathcal{}}$ ${\$에서 얻을$$ 수 있으며$,$ W ${\displaystyle$ w${\$$mathcal$ {$C}$이다$.$

티츠콘은 $X{\displaystyle }$= ${\displaystyle \bigcup _{}}$ ${\displaystyle \underset{}{\mathrm{ww}}}$ ${\displaystyle \underset{}{}}$ ${\displaystyle C}$의${\$ X$=\bigcup _{w\in W}w{\overline{\mathcal{C}}}}}$이다$.$이것이 $∗{\$ V$^{*}}$의 전체일 필요는 없다$.$ 중요한 것은 $X{\displaystyle }$ ${\displaystyle X}$가 볼록하다는 사실이다.$C{\displaystyle \mathcal{}}$ ${\$의 닫힘 $}{\$은(는) X$${\$displaystyle$ X$\}$에서 W$${\$displaystyle W}$의 동작을 위한 기본 도메인이다.

콕시터 콤플렉스

The Coxeter complex ${\displaystyle \Sigma (W,S)}$ of ${\displaystyle W}$ with respect to ${\displaystyle S}$ is ${\displaystyle \Sigma (W,S)=(X\setminus \{0\})/\mathbb {R} _{+}}$, where ${\displaystyle \mathbb {R} _{+}}$ is the multiplicative group of 포지티브 리얼스

예

유한 이면체군

다이헤드 그룹 ${\displaystyle {Dn}_{}}$ ${\$${\displaystyle \mathrm{순서}}$ 2n)은 해당하는 타입 I${\displaystyle {}_{}}$2 (${\displaystyle {\mathrm{}}_{}}$) ${\displaystyle \mathrm$ {$I} _{2}(n)}$의 Coxeter 그룹이다$.$이들은 프레젠테이션 $⟨{\displaystyle s,}$ ${\displaystyle t}$ ${\displaystyle s{}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$,${\displaystyle {}^{}{t\mathrm{}}^{}}$ 2${\displaystyle {}^{}}$,${\displaystyle }$( ${\displaystyle s}$ t${\displaystyle {}^{}}$) ${\displaystyle n^{}}$ ${\displaystyle {}^{}}$ $displaystyle \left\langles,t\,\\,s^{2},(st)^{n}\rigle \right\$$rangle$ \$right$.$}$.

$I{\displaystyle {\mathrm{}}_{}}$ ${\displaystyle {}_{}}$(${\displaystyle n}$) ${\displaystyle \mathrm {I} _{2}(n$$$$)}$의 표준 선형 표현은$$ 평면에서 $n{\displaystyle }$ ${\displaystyle n}$ -곤에$$ 작용하는 것으로서, 이 경우 V${\displaystyle }$= ${\displaystyle {\mathrm{}}^{}}$ $2{\displaystyle }$ ${\$}}{2$}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}{{{{{{{{{{{$2}}}}}}}}예를 들어, 사례 $n{\displaystyle }$= ${\displaystyle 3}$ ${\displaystyle n=3}$에서 타입 ${\displaystyle {\mathrm{}}_{}}$ $2{\displaystyle {\mathrm{}}_{}}$ (${\displaystyle {}_{}3}$)${\displaystyle }$= ${\displaystyle {\mathrm{}}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\$$_{$2}}의 Coxeter 그룹이 평면의 등각 삼각형에 작용한다.각 $반사{\displaystyle }$ s ${\displaystyle s}$에는 이중$$ 벡터 공간(위에서 언급한 바와 같이 이선 $형태{\displaystyle }$ B ${\displaystyle B$을(를) 사용하여 벡터 공간 자체로 표준적으로 식별할 수 있는 연관된 하이퍼플레인 $H{\displaystyle {}_{}}$ ${\displaystyle s_{}}$ ${\$가 있으며$$, 이는 벽이다.아래와 같이 챔버를 절단한다.

Coxeter 콤플렉스는 위의 이미지에서와 같이 해당 ${\displaystyle \mathrm{2n}}$ ${\displaystyle 2n}$ -곤이$$ 된다.이것은 치수 1의 단순한 콤플렉스로, 코타입으로 채색할 수 있다.

무한돌파

또 다른 동기부여의 예로는 무한대 $디헤드{\displaystyle {}_{}}$ 그룹 D$\{\$D_{\$inforty }}$이 있다$.$이는 정수 좌표를 사용하여 점 집합을 보존하는 실제 선의 대칭 집합으로 볼 수 있다.${\displaystyle }x{\displaystyle }$ = ${\displaystyle 0}${\$displaystyle x=0$} $및$ x = ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{2}{}}${\$displaystyle$ x$={1$\1\{1\}}$2}$의 반사에 의해 생성된다.$$이 그룹은 Coxeter 프레젠테이션${\displaystyle presentations,}$ ${\displaystyle t{}^{}}$ ${\displaystyle 2}$, ${\displaystyle {t\mathrm{}}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$⟩ $displaystylease$$\왼쪽\langles s,t\\\왼쪽 \,s^{2},t^{2}\right\angle \right \right.$$}$.

이 경우 $B{\displaystyle }$ ${\displaystyle B}$이(가) 퇴보하므로 이중 공간 $∗{\$ V$^{*}$을(를$)$ 가진 $V$ ${\displaystyle V}$을(를) 더 이상 식별할 수 없다.그런 다음 하이퍼플레인이 정의되어 $있는{\displaystyle {}^{}}$ V $∗{\$ V$^\{*\}\}$만으로 작업하는 것이 좋다.그러면 다음과 같은 그림이 나온다.

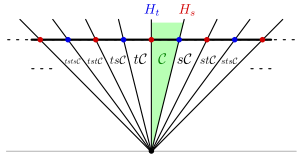
이 경우 티츠 원뿔은 전체 평면이 아니라 상반면일 뿐이다.양수 실수에 의한 지수를 취하면 정수에 표시된 점으로 실제 라인의 또 다른 사본을 산출한다.이것은 무한대 다이헤드 그룹의 콕시터 콤플렉스다.

Coxeter 단지의 대체 시공

Another description of the Coxeter complex uses standard cosets of the Coxeter group ${\displaystyle W}$. A standard coset is a coset of the form ${\displaystyle wW_{J}}$, where ${\displaystyle W_{J}=\langle J\rangle }$ for some subset ${\displaystyle J}$ of ${\displaystyle S}$. For instance, $W{\displaystyle {}_{}}$ ${\displaystyle S{}_{}}$= W ${\displaystyle W_{S}=W}$ 및$$ $W{\displaystyle {}_{}}$ ${\displaystyle {\varnothing \mathrm{}}_{}}$=${\displaystyle }${ ${\displaystyle 1}$} ${\displaystyle W_{\emptyset }=\{1$

Coxeter 복합체 $\sigma {\displaystyle \mathrm{}(W}$, S${\displaystyle }$) ${\displaystyle \Sigma(W,S)}$은 역포함 순서에 따라 표준 코세트의 포셋이다.이것은 다음을 만족시키는 모든 포지션과 마찬가지로 단순화 복합체의 표준 구조를 가지고 있다.

• 어떤 두 원소라도 하한선이 가장 크다.
• 주어진 요소보다 작거나 같은 ${\displaystyle \mathrm{요소}}$의 포셋은 일부 정수 n에 대해 {1$$,${\displaystyle 2}$ ,${\displaystyle }$… , ${\displaystyle n\}}$ ${\displaystyle \{1,2,\ldots ,n\}$의 서브셋 포셋과 이형성이 있다.

특성.

$({\displaystyle W}$, ${\displaystyle S}$) ${\displaystyle (W,S)}$과 연관된 Coxeter 콤플렉스는 ${\displaystyle 치수}$S - ${\displaystyle 1}$ ${\displaystyle$ S $-1}$을(를) 가지고$$ 있다$.$ W가 유한하면${\displaystyle }$(${\displaystyle }$S -${\displaystyle 1}$) ${\displaystyle ($S$-1)$-sphere에$$ 대한 동형이며 W가 무한하면 수축 가능하다.

참고 항목

• 건물들
• 웨일 그룹
• 루트 시스템

참조

• Peter Abramenko와 Kenneth S. Brown, 건물, 이론 및 응용 프로그램.2008년 스프링거