유체 역학의 경계 조건

Boundary conditions in fluid dynamics
추가 정보:계산 유체 역학의 경계 조건

유체 역학의 경계 조건은 계산 유체 역학의 경계 값 문제에 대한 제약 조건의 집합이다.이러한 경계 조건에는 입구 경계 조건, 출구 경계 조건, 벽 경계 조건, 일정한 압력 경계 조건, 축대칭 경계 조건, 대칭 경계 조건 및 주기적 또는 순환 경계 조건이 포함된다.null

일시적 문제에는 한 가지 더 필요한 것이 있는데, 즉 흐름 영역의 노드에서 흐름 변수의 초기 값이 지정되는 초기 조건이다.[1]CFD에서는 다양한 종류의 경계 조건을 서로 다른 조건과 목적으로 사용하고 있으며, 다음과 같이 논의한다.null

흡입구 경계 조건

파이프 내 흡입구 유속 표시

유입구 경계 조건에서는 모든 유량 변수의 분포를 주로 유입구 경계에서 지정해야 한다.[1]이러한 유형의 경계 조건은 공통적이며 대부분 유입구 유속이 알려진 곳에서 지정된다.null

출구경계조건

파이프 내 출구 유속 표시

출구 경계 조건에서는 모든 유량 변수의 분포(주로 유속)를 지정해야 한다.이것은 흡입구 경계 조건과 연계된 것으로 생각할 수 있다.이러한 유형의 경계 조건은 공통적이며 대부분 출구 속도가 알려진 곳에서 지정된다.[1]유량은 기하학적 장애로부터 멀리 떨어진 출구를 선택할 때 흐름 방향에 변화가 없는 완전히 발달된 상태에 도달한다.그러한 지역에서는 출구를 개략적으로 설명할 수 있고 압력을 제외한 모든 변수의 기울기는 흐름 방향에서 0과 동일할 수 있다.null

미끄럼 방지 경계 조건

벽 경계 조건 표시

제한된 유체 흐름 문제에서 가장 흔한 경계는 도관의 벽이다.적절한 요건은 미끄럼 방지 경계 조건이라고 하며, 여기서 속도의 정상 구성요소는 0으로 고정되고 접선 구성요소는 벽의 속도와 동일하게 설정된다.[1]직관에 역행할 수도 있지만, 수십 년의 논란과 논쟁 끝에야 비로소 실험과 이론 양쪽에서 노 슬립 조건이 확고히 자리잡았다.[2]null

벽을 통한 열 전달을 지정할 수 있거나 벽을 단열로 간주할 경우 벽을 통한 열 전달은 0으로 설정된다.null

일정한 압력 경계 조건

일정한 압력 경계 조건 표시

이 유형의 경계조건은 압력의 경계값을 알 수 있고 흐름 분포의 정확한 세부사항을 알 수 없는 경우에 사용된다.여기에는 주로 압력 흡입구 및 배출구 조건이 포함된다.이 경계 조건을 이용하는 대표적인 예로는 부력 구동 흐름, 복수 출구를 가진 내부 흐름, 자유 표면 흐름 및 물체 주위의 외부 흐름이 있다.[1]압력이 대기압인 대기로의 흐름 출구가 그 예다.null

축대칭 경계 조건

축대칭 경계 조건 표시

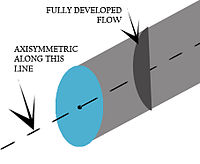
이 경계조건에서 모델은 주축에 관해서 축대칭으로서 특정 r = R, 모든 θs 및 각 z = Z-슬라이스에서 각 흐름 변수가 동일한 값을 갖는다.[3]흐름과 파이프 축이 일치하는 원형 파이프 내의 흐름이 좋은 예다.null


대칭 경계 조건

대칭 경계 조건 표시

이 경계 조건에서는 경계 양쪽에 동일한 물리적 과정이 존재한다고 가정한다.[4]모든 변수는 경계에서 같은 거리에 동일한 값과 구배를 가진다.그것은 반대쪽으로의 모든 흐름 분포를 반영하는 거울의 역할을 한다.[5]대칭 경계의 조건은 경계를 가로질러 흐르지 않으며 경계를 가로질러 스칼라 플럭스가 없다.null

좋은 예가 흐름 속에 대칭적인 장애물이 있는 파이프 흐름이다.장애물은 상류의 흐름과 하류의 흐름을 미러링된 흐름으로 나눈다.null

주기적 또는 주기적 경계 조건

순환 경계 조건을 나타내는 1/4

주기적 또는 주기적 경계 조건은 문제에서 다른 형태의 대칭으로부터 발생한다.구성 요소의 흐름 분포 패턴이 두 번 이상 반복되어 대칭 경계 조건에 필요한 미러 이미지 요구 사항을 위반하는 경우.좋은 예로는 표시된 영역이 r-teta 좌표에서 4회 반복되는 베인 펌프(그림)[6]가 있다.순환 대칭 영역은 동일한 흐름 변수와 분포를 가져야 하며 모든 Z-슬라이스에서 이를 충족해야 한다.[1]null

참고 항목

메모들

  1. ^ a b c d e f Henk Kaarle Versteeg; Weeratunge Malalasekera (1995). An Introduction to Computational Fluid Dynamics: The Finite Volume Method. Longman Scientific & Technical. pp. 192–206. ISBN 0-582-21884-5.
  2. ^ Prabhakara, Sandeep; Deshpande, M. D. (2004-04-01). "The no-slip boundary condition in fluid mechanics". Resonance. 9 (4): 50–60. doi:10.1007/BF02834856. ISSN 0973-712X. S2CID 124269972.
  3. ^ "cyclic symmetric BCs". Retrieved 2015-08-09.
  4. ^ "cyclic symmetric BCs". Retrieved 2013-10-10.
  5. ^ "Symmetric boundary condition".
  6. ^ "cyclic symmetric BCs". Retrieved 2013-10-10.

참조

  • Versteeg (1995). "Chapter 9". An Introduction to Computational Fluid Dynamics The Finite Volume Method, 2/e. Longman Scientific & Technical. pp. 192–206. ISBN 0-582-21884-5.