비트 연산

이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : '비트 조작'– 뉴스 · 신문 · 서적 · 학자 · JSTOR (2018년 8월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

컴퓨터 프로그래밍에서 비트 연산(bitwise operation)은 비트 문자열, 비트 배열 또는 바이너리 숫자(bit string으로 간주)에 대해 개별 비트 수준에서 동작합니다.이것은 빠르고 간단한 동작으로, 상위 수준의 산술 연산에 기본이며 프로세서에서 직접 지원됩니다.대부분의 비트 연산은 입력 오퍼랜드 중 하나를 결과가 대체하는 2개의 오퍼랜드 명령으로 나타납니다.

단순한 저비용 프로세서의 경우 일반적으로 비트 단위 연산은 분할보다 훨씬 빠르고 곱셈보다 몇 배 더 빠르며 경우에 따라서는 덧셈보다 훨씬 더 빠릅니다.최신 프로세서는 명령 파이프라인 및 기타 아키텍처 설계 선택지가 길기 때문에 일반적으로 비트 단위 연산과 같은 속도로 가산 및 곱셈을 수행하지만, 비트 단위 연산에서는 ^[1]리소스 사용이 감소하기 때문에 일반적으로 더 적은 전력을 사용합니다.

비트 연산자

아래 설명에서는 비트의 위치를 나타내는 모든 표시가 오른쪽(중요하지 않은)에서 왼쪽으로 이동합니다.예를 들어 이진수 값 0001(10진수 1)은 첫 번째(즉, 가장 오른쪽)를 제외한 모든 위치에 0이 있습니다.

것은 아니다.

비트 단위 NOT 또는 비트 단위 보완은 각 비트에 대해 논리적 부정을 수행하는 단항 연산으로, 주어진 이진 값에 대한 1개의 보완을 형성합니다.0인 비트는 1이 되고 1인 비트는 0이 됩니다.예를 들어 다음과 같습니다.

NOT 0111(패키지 7) = 1000(패키지 8)

NOT 10101011(패키지 171) = 01010100(패키지 84)

그 결과는 두 사람의 값에서 1을 뺀 값을 더한 것과 같다.만약 2의 보연산을 사용한다면,NOT x = -x − 1.

부호 없는 정수의 경우 숫자의 비트 보수는 부호 없는 정수 범위의 중간 지점에 걸친 숫자의 "미러 반사"입니다.예를 들어, 8비트 부호 없는 정수의 경우,NOT x = 255 - x0 ~ 255의 증가 범위를 255 ~ 0의 감소 범위로 효과적으로 "플립"하는 하향선으로 그래프에 시각화할 수 있습니다.간단하지만 예시적인 사용 예는 각 픽셀이 부호 없는 정수로 저장되는 그레이스케일 이미지를 반전하는 것입니다.

그리고.

4비트 정수의 비트 단위 AND

비트 AND는 2개의 동일한 길이의 바이너리 표현을 사용하여 대응하는 각 비트 쌍에 대해 논리 AND 연산을 수행하는 바이너리 연산입니다.따라서 비교된 위치의 두 비트가 모두 1이면 결과 이진 표현의 비트는 1(1 × 1 = 1)이 되고 그렇지 않으면 결과는 0(1 × 0 = 0 및 0 × 0 = 0)이 됩니다.예를 들어 다음과 같습니다.

0101(패키지 5) 및 0011(패키지 3) = 0001(패키지 1)

이 연산을 사용하여 특정 비트가 (1) 또는 (0)으로 설정되어 있는지 확인할 수 있습니다.예를 들어 비트 패턴 0011(10진수 3)을 지정하면 두 번째 비트가 설정되어 있는지 여부를 판단하기 위해 두 번째 비트에서만 비트 패턴이 1인 AND를 사용합니다.

0011(케이블 3) 및 0010(케이블 2) = 0010(케이블 2)

결과 0010은 0이 아니기 때문에 원래 패턴의 두 번째 비트가 설정되었음을 알 수 있습니다.이것은 종종 비트 마스킹이라고 불립니다(비유적으로 말하면, 변경해서는 안 되는 부분이나 관심 없는 부분을 마스킹 테이프 커버 또는 마스크로 사용하는 것입니다.이 경우 0 값은 관심 없는 비트를 마스킹합니다).

비트 AND는 각 비트가 개별 부울 상태를 나타내는 레지스터의 선택된 비트(또는 플래그)를 지우는 데 사용할 수 있습니다.이 기술은 가능한 한 적은 메모리를 사용하여 다수의 부울 값을 저장하는 효율적인 방법입니다.

예를 들어 0110(10진수 6)은 4개의 플래그의 집합으로 간주할 수 있으며, 여기서 제1 및 제4의 플래그는 클리어(0), 제2 및 제3의 플래그는 세트(1)된다.세 번째 플래그는 세 번째 비트에만 0이 있는 패턴과 함께 비트 AND를 사용하여 지울 수 있습니다.

0110(케이블 6) 및 1011(케이블 11) = 0010(케이블 2)

이 속성으로 인해 가장 낮은 값의 비트의 값을 확인함으로써 이진수의 패리티를 쉽게 확인할 수 있습니다.위의 예를 사용하여 다음을 수행합니다.

0110(표준 6) 및 0001(표준 1) = 0000(표준 0)

6 AND 1은 0이므로 6은 2로 나누어지므로 짝수입니다.

또는

4비트 정수의 비트 단위 OR

비트 단위 OR은 길이가 같은 두 개의 비트 패턴을 취하여 대응하는 각 비트 쌍에 대해 논리적인 포함 OR 연산을 수행하는 이진 연산입니다.두 비트가 모두 0이면 각 위치의 결과가 0이고 그렇지 않으면 결과가 1입니다.예를 들어 다음과 같습니다.

0101(패키지 5) 또는 0011(패키지 3) = 0111(패키지 7)

비트 OR을 사용하여 위에서 설명한 레지스터의 선택된 비트를 1로 설정할 수 있습니다.예를 들어, 0010의 네 번째 비트(10진수 2)는 네 번째 비트만 설정된 패턴으로 비트 단위 OR을 수행하여 설정할 수 있습니다.

0010(케이블 2) 또는 1000(케이블 8) = 1010(케이블 10)

XOR

4비트 정수의 비트 단위 XOR

비트 단위 XOR은 길이가 같은 두 개의 비트 패턴을 취하여 대응하는 각 비트 쌍에 대해 논리 배타적 OR 연산을 수행하는 이진 연산입니다.각 위치의 결과는 비트 중 하나만 1인 경우 1이지만 둘 다 0이거나 둘 다 1인 경우 0이 됩니다.여기에서는 두 비트를 비교합니다.두 비트가 다르면 1이 되고 같으면 0이 됩니다.예를 들어 다음과 같습니다.

0101(패키지 5) XOR 0011(패키지 3) = 0110(패키지 6)

비트별 XOR은 레지스터에서 선택한 비트를 반전하는 데 사용할 수 있습니다(전환 또는 플립이라고도 함).모든 비트는 1로 XOR하여 전환할 수 있습니다.예를 들어 비트 패턴 0010(10진수 2)을 지정하면 두 번째 및 네 번째 비트는 두 번째 및 네 번째 위치에 1을 포함하는 비트 패턴의 비트 단위 XOR에 의해 토글될 수 있습니다.

0010(케이블 2) XOR 1010(케이블 10) = 1000(케이블 8)

이 기술은 부울 상태의 집합을 나타내는 비트 패턴을 조작하기 위해 사용할 수 있습니다.

어셈블리 언어 프로그래머 및 최적화 컴파일러는 레지스터 값을 0으로 설정하는 바로 가기 방법으로 XOR을 사용하는 경우가 있습니다.값에 대해 XOR를 실행하면 항상 0이 됩니다.많은 아키텍처에서 이 동작은 제로 값을 로드하여 레지스터에 저장하는 것보다 적은 클럭사이클과 메모리를 필요로 합니다.

고정길이 n의 비트 문자열 세트(기계어 등)가 ${\displaystyle {필드}_{\mathrm{}}}$ F2$({$$\$displaystyle\$bF${$F}$$_{$2}^{$n$$\})$ 위에 있는 n차원 벡터 $공간{\displaystyle {\mathbf{}}_{}^{}}$ $({$$\bF}_{2})$로 생각되는 경우 벡터 덧셈은 비트 Wise XOR에 대응합니다.

수학적 등가물

음이 아닌 정수에 대해 x${\displaystyle y}$y {\$displaystyle$x\$geq$ y$\}$라고 가정하면 다음과 같이 비트 연산을 쓸 수 있습니다.

${\displaystyle{\begin{정렬}\operatorname{NOT}x&, =\sum _ᆮ^ᆯ())\rfloor}2^ᆰ\left[\left(\left\lfloor{\frac{x}{2^{n}}}\right\rfloor{\bmod{2}}+1\right){\bmod{2}}\right]=2^ᆱ())\right\rfloor+1}-1-x\\x\operatorname{AND}y&, =\sum _ᆳ^ᆴ())\rfloor}2^{n}\left(\left\lfloor{\fr.교류{)}{2^{n}}}\right\rfloor{\bmod{2}}\right)\left(\left\lfloor{\frac{y}{2^{n}}}\right\rfloor{\bmod{2}}\right)\\x\operatorname{OR}y&, =\sum _ᆯ^ᆰ())\rfloor}2^ᆱ\left(\left는 경우에는 \left(\left\lfloor{\frac{x}{2^{n}}}\right\rfloor{\bmod{2}}\right)+\left(\left\lfloor{\frac{y}{2^{n}}}\right\rfloor{\bmod{2}}\right)+\left(\left\lfl.oor{\frac {x} {2^{n}} \ rfloor {bmod {2} \ right ( \ lfloor { 2 ^ {n} ) \ right \ rfloor { bmod {2} \ right } \ bmod {2} \ x \ operatorname {X }OR}y&, =\sum _ᆬ^ᆭ())\rfloor}2^ᆮ\left(\left[\left(\left\lfloor{\frac{x}{2^{n}}}\right\rfloor{\bmod{2}}\right)+\left(\left\lfloor{\frac{y}{2^{n}}}\right\rfloor{\bmod{2}}\right)\right]{\bmod{2}}\right)=\sum _ᆯ^ᆰ())\rfloor}2^{n}\left는 경우에는 \left(\left\lfloor{\frac{)}{2^{n}}}\right\rfloor +\left\lflo.또는{\frac {y}{2^{n}}\right\cloor\right}{\bmod {2}}\right}\end {aligned}}$

모든 이진 논리 연산자에 대한 진실 표

2개의 이진수 변수에는 16개의 진위 함수가 있으며, 이는 진위 테이블을 정의합니다.

다음으로 2비트 P와 Q의 비트 단위 등가 연산을 나타냅니다.

비트 시프트

비트 시프트는 값을 수치가 아닌 일련의 비트로 취급하기 때문에 비트 단위 연산으로 간주될 수 있습니다.이러한 조작에서는, 숫자가 왼쪽 또는 오른쪽으로 이동하거나 이동됩니다.컴퓨터 프로세서의 레지스터는 고정된 폭을 가지므로 일부 비트는 레지스터에서 "쉬프트 아웃"되는 반면, 같은 수의 비트는 다른 쪽 끝에서 "쉬프트 인"됩니다. 비트 시프트 연산자 간의 차이는 시프트 인 비트의 값을 결정하는 방법에 있습니다.

비트 어드레싱

레지스터의 폭(흔히 32 또는 심지어 64)이 종종 바이트라고 불리는 최소 주소 지정 가능 단위의 비트 수(통상 8)보다 클 경우, 시프트 연산은 바이트에서 비트로 주소 지정 방식을 유도한다.따라서 자리수 표기법에서 숫자의 표준 표기법에서 "왼쪽"과 "오른쪽" 방향을 취함으로써 왼쪽 시프트가 증가하고 오른쪽 시프트가 숫자의 값을 감소시킵니다. 왼쪽 자릿수를 먼저 읽으면 빅 엔디안이 됩니다.레지스터의 양단에서 경계 효과를 무시하면 산술 및 논리 시프트 연산은 동일하게 동작하며, 8비트 위치별 시프트는 다음과 같은 방법으로 비트 패턴을 1바이트 위치만큼 전송합니다.

리틀 엔디안 주문:	8개의 위치를 왼쪽으로 이동하면 바이트 주소가 1씩 증가합니다.
	8개의 위치를 오른쪽으로 이동하면 바이트 주소가 1개씩 감소합니다.
빅엔디안 오더:	8개 위치만큼 왼쪽으로 이동하면 바이트 주소가 1개씩 감소합니다.
	8개의 위치를 오른쪽으로 이동하면 바이트 주소가 1씩 증가합니다.

산술 시프트

좌측 산술 시프트

우측 산술 시프트

산술 시프트에서는 어느 한쪽 끝에서 시프트된 비트는 폐기됩니다.왼쪽 산술 시프트에서는 0이 오른쪽으로 이동하며, 오른쪽 산술 시프트에서는 부호 비트(2의 보수의 MSB)가 왼쪽으로 이동하므로 피연산자의 부호가 유지됩니다.

이 예에서는 8비트 레지스터를 사용하고 있습니다.이 레지스터는 2의 보완으로 해석됩니다.

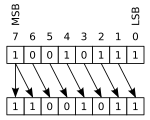
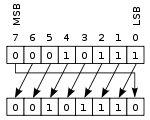
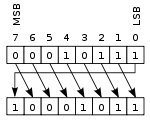
00010111(표준 +23) LEFT-SHIFT = 00101110(표준 +46)

10010111 (표준 -105) RIGHT-SHIFT = 11001011 (표준 -53)

첫 번째 예에서는 왼쪽 끝자리가 레지스터의 끝을 지나 새로운 0이 오른쪽 위치로 이동되었습니다.두 번째 예에서는 맨 오른쪽 1이 (아마도 캐리 플래그에) 어긋나고 새로운 1이 맨 왼쪽 위치에 복사되어 번호의 기호가 유지됩니다.복수의 시프트가 1개의 시프트로 몇 자리수 단축되는 경우가 있습니다.예를 들어 다음과 같습니다.

00010111(표준 +23) LEFT-SHIFT-BY-TWO = 01011100(표준 +92)

왼쪽 산술 시프트에 n을 곱하는 것은 2를ⁿ 곱하는 것과 같으며(값이 오버플로하지 않는 한), 오른쪽 산술 시프트에 n을 곱하는 것은 2를 곱하는ⁿ 것과 같다.이진수가 1의 보완으로 처리될 경우 동일한 오른쪽 이동 연산을 통해 2로ⁿ 나누고 0으로 반올림합니다.

논리 시프트

좌측 논리 시프트

우측 논리 시프트

논리 시프트에서는 폐기된 비트를 대체하기 위해 0이 시프트됩니다.따라서 논리좌변환과 산술좌변환은 완전히 동일합니다.

그러나 논리 오른쪽 시프트는 부호 비트를 복사하는 대신 값 0비트를 최상위 비트에 삽입하므로 부호 없는 2진수에는 이상적이며 산술 오른쪽 시프트는 부호 있는 2진수에는 이상적입니다.

순환 이동

이동의 또 다른 형태는 원형 이동, 비트 회전 또는 비트 회전입니다.

회전

왼쪽 원형 이동 또는 회전

우측 원형 이동 또는 회전

Rotate No Carry라고도 하는 이 동작에서는 레지스터의 왼쪽 끝과 오른쪽 끝이 결합된 것처럼 비트가 "회전"됩니다.왼쪽 이동 중에 오른쪽으로 이동되는 값은 왼쪽에서 이동된 값이며 오른쪽 이동 작동의 경우 그 반대의 값입니다.이는 기존의 모든 비트를 유지할 필요가 있을 때 유용하며 디지털 ^{[clarification needed]}암호화에 자주 사용됩니다.

캐리를 통해 회전

좌측 회전 캐리

캐리를 통해 우측 회전

Rotate through Carry는 회전 동작의 변형입니다. 여기서 (양쪽 끝에서) 시프트된 비트는 반송 플래그의 이전 값이고, 시프트된 비트는 반송 플래그의 새 값이 됩니다.

한 번의 회전으로 캐리 플래그를 미리 설정하여 한 위치의 논리적 또는 산술적 시프트를 시뮬레이션할 수 있습니다.예를 들어, carry 플래그가 0을 포함하는 경우x RIGHT-ROTATE-THROUGH-CARRY-BY-ONE는 논리적인 우측 이동이며, carry 플래그가 부호 비트의 복사본을 포함하는 경우,x RIGHT-ROTATE-THROUGH-CARRY-BY-ONE산술적 우측 변속입니다.이러한 이유로 로우엔드 PIC와 같은 일부 마이크로 컨트롤러는 회전 및 회전만 수행하므로 산술적 또는 논리적 시프트 명령이 필요하지 않습니다.

Rotate through Carry는 프로세서의 네이티브 워드 크기보다 큰 숫자의 시프트를 실행할 때 특히 유용합니다.대수가 2개의 레지스터에 저장되어 있는 경우 첫 번째 레지스터의 한쪽 끝에서 시프트된 비트가 두 번째 끝에 있어야 하기 때문입니다.Rotate-Through-Carry를 사용하면 첫 번째 교대 근무 중에 해당 비트가 "저장"되어 별도의 준비 없이 두 번째 교대 근무 중에 교대할 수 있습니다.

고급 언어

C 패밀리 및 Python

C 패밀리 언어에서 논리 시프트 연산자는 다음과 같습니다.<<왼쪽 시프트의 경우>>오른쪽 시프트를 위해.이동할 장소의 수는 연산자에게 두 번째 인수로 지정됩니다.예를들면,

x = y << > 2; 

할당하다x이동의 결과y왼쪽으로 2비트, 즉 4의 곱셈과 같습니다.

시프트를 사용하면 구현 정의 동작 또는 정의되지 않은 동작이 발생할 수 있으므로 사용할 때 주의해야 합니다.단어 크기보다 크거나 같은 비트 수만큼 이동한 결과는 C 및 C++^[2][3]에서 정의되지 않은 동작입니다.음수 값은 구현에서 정의되며 모범 코딩 ^[4]관행에서는 권장되지 않습니다. 결과 ^[2]유형으로 결과를 나타낼 수 없는 경우 부호 있는 값을 왼쪽으로 전환하는 결과는 정의되지 않습니다.

C#에서 오른쪽 시프트는 첫 번째 피연산자가 int 또는 long일 때의 산술 시프트입니다.첫 번째 피연산자가 uint 또는 ulong 유형인 경우 오른쪽 시프트는 논리적 ^[5]시프트입니다.

순환 교대

C 계열의 언어에는 회전 연산자가 없습니다(단, C++20은std::rotl그리고.std::rotr). 단, 1개는 교대 연산자에서 합성할 수 있습니다.보안 ^[6]요건이 있는 소프트웨어에서 정의되지 않은 동작 및 타이밍 공격을 방지하기 위해 스테이트먼트가 올바르게 형성되도록 주의해야 합니다.예를 들어 32비트 부호 없는 값을 좌회전시키는 단순한 구현입니다.x타고n입장은 단순하다

uint32_t x = ..., n = ...; uint32_t y = (x << > n)   (x >> (32 - n)); 

하지만, 다음 시프트는0비트는 정의되지 않은 동작을 오른쪽 식에서 발생시킵니다.(x >> (32 - n))왜냐면32 - 0이32,그리고.320 ~ 31 의 범위를 벗어납니다.두 번째 시도에서는 다음과 같은 결과가 발생할 수 있습니다.

uint32_t x = ..., n = ...; uint32_t y = n ? (x << > n)   (x >> (32 - n)) : x; 

여기서 시프트량은 정의되지 않은 동작을 발생시키지 않도록 테스트됩니다.단, 브랜치에서는 코드 패스가 추가되어 타이밍 분석과 공격의 기회가 생깁니다.이는 높은 무결성 ^[6]소프트웨어에서는 허용되지 않는 경우가 많습니다.게다가 코드는, 프로세서의 네이티브 명령보다 효율이 낮은 복수의 머신 명령으로 컴파일 됩니다.

정의되지 않은 동작과 GCC 및 Clang 아래에 있는 브랜치를 피하기 위해 다음 사항을 권장합니다.이 패턴은 많은 컴파일러에서 인식되며 컴파일러는 1회 회전 ^[7][8][9]명령을 실행합니다.

uint32_t x = ..., n = ...; uint32_t y = (x << > n)   (x >> (-n & 31)); 

Microsoft Visual C++의 _rotl8, _rotl16, _rotr8, _rotr16과 같은 순환 시프트를 구현하는 컴파일러 고유의 함수도 있습니다.Clang은 ^[9]위의 문제를 겪고 있는 Microsoft 호환성을 위해 몇 가지 회전 기능을 제공합니다.GCC는 회전 함수를 제공하지 않습니다.인텔은 x86 내장 기능도 제공합니다.

자바

자바에서는 모든 정수형이 부호화되어 있기 때문에<<" 및 ">>연산자는 산술 시프트를 수행합니다.Java가 연산자 "를 추가합니다.>>>"논리적인 오른쪽 시프트를 실행하는데, 논리적인 왼쪽 시프트 연산과 산술적인 왼쪽 시프트 연산은 부호 있는 정수에 대해 동일하기 때문에 "는 없습니다.<<<자바 연산자.

Java shift ^[10]연산자에 대한 자세한 내용은 다음과 같습니다.

• 연산자<<(좌회전),>>(서명된 우측 시프트), 및>>>(지정된 오른쪽 이동)을 이동 연산자라고 합니다.
• shift 식의 유형은 왼쪽 피연산자의 승격 유형입니다.예를들면,aByte >>> 2와 동등하다((int) aByte) >>> 2.
• 좌측 피연산자의 승격 타입이 int일 경우 우측 피연산자의 하위 비트 5개만 시프트 거리로 사용됩니다.이는 마치 우측 오퍼랜드에 0x1f(0b111)^[11]의 마스크 값을 갖는 비트 논리 AND 연산자를 부여한 것과 같다.따라서 실제로 사용되는 시프트 거리는 항상 0 ~31의 범위 내에 있습니다.
• 왼쪽 피연산자의 승격 유형이 길면 오른쪽 피연산자의 하위 6비트만 시프트 거리로 사용됩니다.이는 마치 우측 오퍼랜드에 0x3f(0b11111)^[11]의 비트 논리 AND 연산자를 부여한 것과 같다.따라서 실제로 사용되는 시프트 거리는 항상 0 ~63의 범위 내에 있습니다.
• 가치n >>> s는 0의 오른쪽 방향의 비트 위치입니다.
• 비트 및 시프트 작업에서 유형은byte암묵적으로 변환되다int바이트 값이 음수일 경우, 가장 높은 비트가 1이고, 1이 int의 추가 바이트를 채우기 위해 사용됩니다.그렇게byte b1 = -5; int i = b1 0x0200;결과적으로i == -5.

자바스크립트

JavaScript는 비트 연산을 사용하여 두 개 이상의 유닛 각각을 1 또는 ^[12]0으로 평가합니다.

파스칼

파스칼과 그 모든 방언(오브젝트 파스칼, 스탠다드 파스칼 등)에서 논리 좌/우 이동 연산자는 다음과 같습니다.shl" 및 "shr" " 를 참조해 주세요.부호 있는 정수라도shr는 논리적인 이동처럼 동작하며 부호 비트를 복사하지 않습니다.두 번째 인수로 이동할 장소의 수를 제시합니다.예를 들어, 다음은 y를 왼쪽으로 2비트 이동한 결과 x를 할당합니다.

x := y 할 수 있다 2; 

다른.

• popcount, 암호화에 사용
• 선행 0을 세다

적용들

비트 연산은 장치 드라이버, 로우 레벨 그래픽스, 통신 프로토콜 패킷 어셈블리 및 디코딩과 같은 하위 레벨 프로그래밍에서 특히 필요합니다.

기계에는 종종 산술 연산과 논리 연산을 수행하기 위한 효율적인 명령어가 내장되어 있지만, 이러한 모든 연산은 다양한 방법으로 ^[13]비트 연산자와 제로 테스트를 조합하여 수행할 수 있습니다.예를 들어, 여기 두 개의 임의의 정수를 곱하는 방법을 보여주는 고대 이집트 곱셈의 유사 코드 구현이 있다.a그리고.b(a보다 크다b) 비트 시프트 및 덧셈만 사용합니다.

c ← 0 하는 동안에 b ≠ 0     한다면 (b 그리고. 1) ≠ 0         c ← c + a     왼쪽 교대하다 a 타고 1     맞다 교대하다 b 타고 1 돌아가다 c 

또 하나의 예는 덧셈의 의사코드 실장입니다.이것은 2개의 정수의 합을 계산하는 방법을 나타내고 있습니다.a그리고.b비트 연산자와 제로 큐를 사용합니다.

하는 동안에 a ≠ 0     c ← b 그리고. a     b ← b xor a     왼쪽 교대하다 c 타고 1     a ← c 돌아가다 b 

부울 대수

컴파일러 쓰기 등 비트 연산으로 구성된 복잡한 식을 단순화하는 것이 유용할 수 있습니다.컴파일러의 목적은 높은 수준의 프로그래밍 언어를 가능한 한 효율적인 기계 코드로 변환하는 것입니다.부울 대수는 복잡한 비트 표현식을 단순화하는 데 사용됩니다.

그리고.

• x & y = y & x
• x & (y & z) = (x & y) & z
• x & 0xFFFF = x^[14]
• x & 0 = 0

• x & x = x

또는

• x y = y x
• x (y z) = (x y) z
• x 0 = x
• x 0xFFFF = 0xFFFF
• x x = x

것은 아니다.

• ~(~x) = x

XOR

• x ^ y = y ^ x
• x ^ (y ^ z) = (x ^ y) ^ z
• x ^ 0 = x
• x ^ y ^ y = x
• x ^ x = 0
• x ^ 0xFFFF = ~x

또한 XOR은 3가지 기본 연산(AND, OR, NOT)을 사용하여 구성할 수 있습니다.

• a ^ b = (a b) & (~a ~b)
• a ^ b = (a & ~b) (~a & b)

다른이들

• x (x & y) = x
• x & (x y) = x
• ~(x y) = ~x & ~y
• ~(x & y) = ~x ~y
• x (y & z) = (x y) & (x z)
• x & (y z) = (x & y) (x & z)
• x & (y ^ z) = (x & y) ^ (x & z)
• x + y = (x ^ y) + ((x & y) << 1)
• x - y = ~(~x + y)

역수식과 해법 방정식

부울대수의 변수에는 풀기가 어려울 수 있습니다. 왜냐하면 정규대수와 달리 몇몇 연산에는 역수가 없기 때문입니다.인버전이 없는 조작은 실행 시 원본 데이터 비트의 일부를 손실하고 이 누락된 정보를 복구할 수 없습니다.

• 역수를 가지다
  • 것은 아니다.
  • XOR
  • 왼쪽으로 회전
  • 오른쪽으로 회전
• 반전 없음
  • 그리고.
  • 또는
  • 왼쪽으로 이동
  • 오른쪽으로 이동

작업 순서

이 목록의 맨 위에 있는 작업이 먼저 실행됩니다.자세한 목록은 메인 문서를 참조하십시오.

• ( )
• ~ -^[15]
• * / %
• + -^[16]
• << >>
• &
• ^

「 」를 참조해 주세요.

레퍼런스

외부 링크

• Online Bitwise Calculator는 Bitwise AND, OR 및 XOR을 지원합니다.
• 비트 단위 XOR 파일/스트림용 도구인 XORcat
• 비트 시프트를 사용한 나눗셈
• 울프램 데모 프로젝트 엔리케 젤레니의 "비트 운영 모델 N"
• 울프람 시연 프로젝트 엔리케 젤레니의 "비트 연산의 구성도"