수직 압력 변화

수직 압력 변동은 상승 함수로서 압력의 변동이다. 문제의 액체와 언급되는 맥락에 따라, 그것은 또한 고도에 수직인 차원에서도 크게 다를 수 있으며, 이러한 변화는 압력 경사 힘과 그 영향의 맥락에서 관련성을 가진다. 그러나 수직 변화는 유체에 대한 중력의 당김으로 인해 발생하기 때문에 특히 중요하다. 즉, 동일한 유체의 경우, 유체 내부의 고도가 감소하는 것은 그 지점을 짓누르는 더 높은 유체 기둥에 해당한다.

기본식

수직 유체 압력 변동의 비교적 간단한 버전은 단순히 두 표고 사이의 압력 차이가 표고 변화, 중력 및 밀도의 산물이라는 것이다. 방정식은 다음과 같다.

${\displaystyle \frac{d}{}}$ P ${\displaystyle \frac{d}{}}$ ${\displaystyle \frac{}{}}$= -${\displaystyle \rho }$ ${\displaystyle g}$ ${\displaystyle {\frac {dP}{dh}=-\rho g}$및

어디에

P는 압박이다.

ρ은 밀도,

g는 중력의 가속이다.

h는 키다.

델타 기호는 주어진 변수의 변화를 나타낸다. g는 음수이므로 키의 증가는 압력 감소에 해당하며, 이는 앞에서 언급한 유체 기둥의 무게에 대한 추론과 들어맞는다.

밀도와 중력이 근사적으로 일정할 때(즉, 비교적 작은 높이의 변화에 대해) 단순히 높이 차이, 중력 및 밀도를 곱하면 압력 차이의 근사치가 충분하다. 다른 액체가 서로 위로 층을 이루는 경우, 총 압력 차이는 두 가지 압력 차이를 추가함으로써 얻을 수 있을 것이다. 첫째는 지점 1에서 경계 2까지, 둘째는 경계에서 지점 2까지이다. 즉 각 액에 대한 for과 Δh 값을 대체하고 결과의 합을 취한다. 유체의 밀도가 높이에 따라 다르다면 수학적 통합이 필요할 것이다.

밀도와 중력을 상수로 합리적으로 근사하게 추정할 수 있는지는 중력과 밀도 또한 고도가 높을수록 감소하기 때문에 필요한 정확도뿐만 아니라 높이 차이의 길이 척도에도 달려 있다. 특히 밀도의 경우, 문제의 액체는 또한 관련이 있다; 예를 들어, 바닷물은 압축할 수 없는 액체로 간주된다; 그 밀도는 높이에 따라 달라질 수 있지만 공기의 그것보다 훨씬 덜하다. 따라서 물의 밀도는 공기의 밀도보다 상수만큼 합리적으로 근사할 수 있으며, 동일한 높이 차이를 감안할 때 물의 압력 차이는 어느 높이에서나 대략 동일하다.

정수역 역설

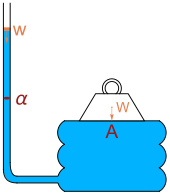
기압식은 유체실 높이에만 의존하며, 그 폭이나 길이에 의존하지 않는다. 충분히 큰 높이를 제공하면 어떤 압력도 얻을 수 있다. 이러한 수력학의 특징은 정수역학 역설이라고 불려왔다. W. H. Besant에 의해 표현된 바와 같이,^[2]

어떤 양의 액체는 아무리 작더라도, 아무리 크더라도 무게를 지탱하기 위해 만들어질량이 크더라도 말이다.

네덜란드의 과학자 사이먼 스테빈은 역설의 수학적인 설명을 가장 먼저 했다.^[3] 1916년 리차드 글래즈브룩은 파스칼에 기인한 배열: 무거운 무게 W가 단면적 α의 수직관에 연결된 유체 방광 위에 놓여 있는 판자에 놓여 있는 것을 설명하면서 정수 역설을 언급했다. 튜브 아래로 무게의 물을 붓는 것은 결국 무거운 무게를 증가시킬 것이다. 힘의 균형이 방정식으로 이어진다.

${\displaystyle W={\frac {wA}{\alpha }}.}$

글레이즈브룩은 "보드의 면적이 상당하고 튜브의 면적이 작아짐으로써 큰 무게 W는 작은 무게 w의 물로 지탱할 수 있다. 이 사실은 때로 정수 역설로 묘사되기도 한다."^[4]

정수 역설에 대한 실증 실험은 그 현상을 가르치는 데 사용된다.^[5][6]

지구 대기의 맥락에서

만약 지구 대기의 수직 압력 변동을 분석한다면, 길이 척도는 매우 유의하며(트로피권만 몇 킬로미터, 열권은 몇 백 킬로미터) 관련 유체(공기)는 압축 가능하다. 평균적으로 약 6371km인 지구의 반지름에 비해 킬로미터의 순서에 따른 길이 척도가 여전히 작고,^[7] 중력은 지구 중심부로부터의 거리의 함수이기 때문에 중력은 여전히 상수로 합리적으로 근사할 수 있다.^[8]

반면에 밀도는 높이에 따라 더 크게 달라진다. 라는 이상적 가스 법칙에서 따온 것이다.

${\displaystyle \rho ={\frac {mP}{kT}},}$

어디에

m은 공기 분자당 평균 질량이다.

P는 주어진 지점에서 압력이다.

k는 볼츠만 상수인데

T는 켈빈 단위로 표시한 온도다.

더 간단히 말해서, 공기 밀도는 기압에 달려있다. 기압도 공기 밀도에 따라 달라진다는 점에서 이것이 순환 정의라는 인상을 받기는 쉬울 것이지만, 단순히 다른 변수의 상호의존성일 뿐이다. 이렇게 하면 보다 정확한 형식의 공식을 얻을 수 있다.

${\displaystyle P_{h}=P_{0}e^{-{\frac {mgh}{kT}},}$

어디에

P는_h 높이 h에서의 압력이다.

P는₀ 기준점 0에서의 압력(일반적으로 해수면 참조)이다.

m은 공기당 질량이다.

g는 중력에 의한 가속이다.

h는 기준점 0으로부터의 높이,

k는 볼츠만 상수인데

T는 켈빈 단위로 표시한 온도다.

따라서 압력은 "기본 공식" 섹션에 제시된 보다 단순한 공식에서 기대할 수 있는 키의 선형 함수보다는 높이의 지수 함수로 더 정확하게 표현된다.

이러한 단순화에서는 온도가 높이에 따라 달라지더라도 온도가 일정하게 처리된다는 점에 유의하십시오. 그러나 대기의 하부층(트로피어, 성층권) 내의 온도 변동은 수십 도 이내일 뿐, 수백 도 이내인 열역학적 온도와는 대조적이기 때문에 온도 변동은 합리적으로 작아서 무시된다. (CN 타워와 같은) 가장 높은 건물들의 위아래를 포함한 더 작은 높이 차이나 비슷한 크기의 산의 경우, 온도 변화는 쉽게 한 자리 수 내에 있을 것이다. (유효율을 참조하십시오.)

포틀랜드 주 항공우주 협회에 의해 보여지는 대안적 파생은 대신 압력의 함수로 높이를 주는 데 사용된다.^[9] 이것은 역직관에 반하는 것처럼 보일 수 있는데, 압력은 그 반대보다는 높이에 기인하기 때문이다. 그러나 그러한 공식은 전자가 아닌 후자를 알고 있을 때 압력의 차이에 근거한 높이를 찾는 데 유용할 수 있다. 다른 종류의 근사치에 대해 다른 공식들이 제시된다. 이전 공식과 비교하기 위해, 본 문서에서 처음 언급된 공식은 동일한 상온 근사치를 적용하는 공식일 것이다. 이 경우:

${\displaystyle z=-{\frac {RT}{g}}{g}\ln {\frac {P}{P_{0}}}}}}}}$

(기사에 사용된 값 포함)

z는 미터 단위의 고도,

R은 특정 가스 상수 = 287.053 J/(kg K)

T는 해발에서 켈빈 = 288.15K의 절대 온도,

g는 해수면에서 중력에 의한 가속도 = 9.80665 m/s이다².

P는 Pascals에서 표고 z의 주어진 지점에 있는 압력이다.

P는₀ 기준점에서의 압력 = 해수면에서의 101,325 Pa이다.

같은 글에서 도출된 보다 일반적인 공식은 기온의 선형 변화를 키 함수(후퇴율)로 설명하며, 온도가 일정할 때 위쪽으로 감소한다.

${\displaystyle z={\frac {T_{0}}{L}\좌측(\frac {P}{P_{0}}\우측)^{-{\frac {LR}{g}-1\우측)}}$

어디에

L은 대기권 소멸률(가로 나눈 온도 변화) = -6.5×10⁻³ K/m이며,

T는₀ P = P와₀ 동일한 기준점의 온도다.

그리고 다른 수량은 위의 수량과 동일하다. 이것은 사용하기에 권장되는 공식이다.

참고 항목

• 기압계
• 효소 방정식
• 파스칼 통
• 루이나 몬티움
• 압력 그라데기
• 시폰

참조

• Merlino, Robert L. (2003). "Statics – Fluids at rest". Retrieved 2014-11-20.