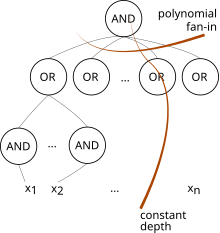
AC0

AC0
AC0 회로 다이어그램:n 입력 비트는 하단에 있고 상단 게이트는 출력을 생성하며, 회로는 각각 다항식 팬인 AND-와 OR-게이트로 구성되며, 교류 깊이는 상수로 경계를 이룬다.

AC는0 회로 복잡성에 사용되는 복잡도 등급이다.AC 계층 구조에서 가장 작은 등급이며, 모든 깊이 O(1)와 다항식 크기의 회로 계열로 구성되며, 무제한 팬닌 AND 게이트와 OR 게이트(입력 시에만 게이트를 허용하지 않음)가 있다.[1]바운드 파닌 AND와 OR 게이트만 있는 NC를0 담았다.[1]

예시 문제

정수 덧셈과 뺄셈은 AC에서0 계산할 수 있지만,[2] 곱셈은 (적어도 정수의 일반적인[3] 이진법이나 베이스-10 표현에서는 안 된다.)

P/폴리처럼 회로수업이기 때문에 AC도0 모든 단항어를 포함하고 있다.

서술적 복잡성

서술적 복잡성의 관점에서, DLOGTIME-통일 AC는0 기술 클래스 FO+B와 같다.모든 언어의 IT는 1차 로직에서 BIT 술어가 추가되거나 FO(+, ×) 또는 로그 계층 구조에서 Turing machine에 의해 설명될 수 있다.[4]

분리

1984년 퍼스트, 작센, 시퍼는 입력의 패리티를 계산하는 것은 균일하지 않더라도 어떤 AC0 회로로도 결정할 수 없다는 것을 보여주었다.[5][1]후자의 회로 계열이 패리티를 계산할 수 있기 때문에 AC는0 NC와1 같지 않다.[1]보조정리 전환은 좀 더 정확한 범위를 따른다.이를 활용하면 다항식 계층 구조와 PSPACE 사이에 Oracle의 분리가 있는 것으로 나타났다.

참조

  1. ^ a b c d Arora, Sanjeev; Barak, Boaz (2009). Computational complexity. A modern approach. Cambridge University Press. pp. 117–118, 287. ISBN 978-0-521-42426-4. Zbl 1193.68112.
  2. ^ Barrington, David Mix; Maciel, Alexis (July 18, 2000). "Lecture 2: The Complexity of Some Problems" (PDF). IAS/PCMI Summer Session 2000, Clay Mathematics Undergraduate Program: Basic Course on Computational Complexity.
  3. ^ Kayal, Neeraj; Hegde, Sumant (2015). "Lecture 5: Feb 4, 2015" (PDF). E0 309: Topics in Complexity Theory. Archived (PDF) from the original on 2021-10-16. Retrieved 2021-10-16.
  4. ^ Immerman, N. (1999). Descriptive Complexity. Springer. p. 85.
  5. ^ Furst, Merrick; Saxe, James B.; Sipser, Michael (1984). "Parity, circuits, and the polynomial-time hierarchy". Mathematical Systems Theory. 17 (1): 13–27. doi:10.1007/BF01744431. MR 0738749. Zbl 0534.94008.