1/3–2/3 추측

1/3–2/3 conjecture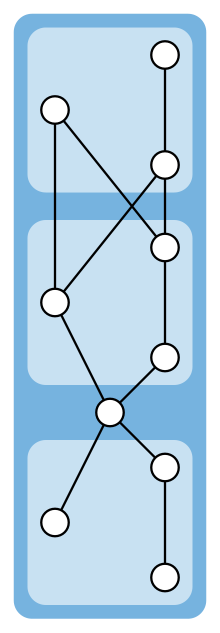
1element와 3element 부분 오더의 직렬 구성으로 형성된 부분 순서. 27개의 선형 확장 중에서 왼쪽 하단 요소는 27개 중 9개에서 오른쪽 하단 요소보다 먼저 발생한다. 이 구조를 가진 부분적인 주문은 1/3-2/3 추측에 대해 알려진 유일한 극단적인 경우다.

수학의 한 분야인 이론, 1/3–2/3 추측에 따르면, 만약 어떤 것이 항목 집합을 분류하는 비교라면, 어떤 비교가 이미 수행되었든 간에, 2/3 이상의 인수에 의해 가능한 정렬 순서 수를 줄일 수 있는 방법으로 다음 비교를 선택하는 것이 항상 가능하다고 한다. 동등하게, 완전히 순서가 정해지지 않은 모든 유한 부분 순서에, 부분 순서의 선형 확장의 최소 1/3과 최대 2/3이 y보다 먼저 x인 속성이 있는 원소 x와 y의 쌍이 존재한다.

예

단일 비교가능성 관계인 ≤ b로 a, b, c의 세 요소에 의해 형성된 부분 순서는 ≤ b ≤ c, ≤ c ≤ b, c b a ≤ b의 세 개의 선형 확장을 가지고 있다. 이 세 확장자 모두에서 a는 b보다 빠르다. 그러나 그 중 단 2개에서 a가 c보다 빠르며, 3번째에서 c보다 늦다. 따라서 a와 c의 쌍은 원하는 특성을 가지며, 이러한 부분적인 순서는 1/3–2/3 추측에 부합함을 보여준다.

이 예는 추측의 상수 1/3과 2/3이 팽팽하다는 것을 보여준다; 만약 q가 1/3과 2/3 사이의 어떤 부분이라면, 전체 부분 순서 수의 q와 1 - q 사이에 있는 여러 부분 순서에서 x가 y보다 빠른 쌍 x는 존재하지 않을 것이다.[1]

보다 일반적으로 P는 그림의 부분 순서와 같이 3개 요소 부분 순서와 1개 요소 부분 순서의 모든 시리즈 구성이 되도록 한다. 그 후 P는 각 원소의 쌍 x, y에 대해 P의 선형 확장의 대부분 1/3에서 다른 원소보다 먼저 두 원소 중 하나가 발생한다는 점에서 1/3–2/3 추정에 대한 극단적인 경우를 형성한다. 이 구조를 가진 부분 순서는 반드시 직렬-병렬 반차순이다. 그것들은 추측과 ca에 대해 알려진 유일한 극단적인 경우다.n은 폭 2의 유일한 극단적인 경우로 입증된다.[2]

정의들

부분적으로 순서가 정해진 집합은 반사적, 비대칭적, 전이적인 이진관계 ≤과 함께 집합 X이다. 전체 순서는 모든 요소 쌍이 비교 가능한 부분 순서다. 유한 부분 순서의 선형 확장은 X의 원소를 순차적으로 배열하는 것으로, x y y가 부분 순서로 되어 있으면, x가 선형 확장에서 y보다 먼저 와야 하는 속성이 있다. 즉 부분 순서와 양립할 수 있는 토탈 오더라는 것이다. 유한 부분 순서 집합을 완전히 정렬하면 선형 확장이 한 개뿐이지만 그렇지 않으면 둘 이상이다. 1/3-2/3 추측에 따르면, 이러한 가능한 선형 확장의 집합 중 1/3과 2/3 사이에 y보다 먼저 x를 배치하고, 1/3과 2/3 사이에 대칭적으로 y를 x보다 먼저 배치하는 두 개의 원소 x와 y를 선택할 수 있다.[3]

확률론 언어에는 1/3–2/3 추측에 대한 대안적이고 동등한 진술이 있다. 각 가능한 선형 확장이 동일하게 선택될 가능성이 있는 선형 확장에 균일한 확률 분포를 정의할 수 있다. 1/3–2/3 추측에 따르면, 이 확률 분포에 따라 무작위 선형 확장에서 x가 y보다 빠를 확률은 1/3과 2/3 사이일 정도로 x와 y 원소의 쌍이 존재한다고 한다.[3]

Kahn & Saks(1984)는 부분적으로 순서가 정해진 P에 대해 Δ(P)를 Δ(최대 실수 Δ)로 정의하는데, 이는 전체 선형 확장의 Δ에서 Δ와 1 Δ 사이에 있는 선형 확장의 수에서 P가 y보다 앞 x 쌍 x를 갖는 것이다. 이 표기법에서 1/3–2/3 추측에 따르면 총계가 아닌 모든 유한 부분 순서는 Δ(P) 1/3이 있다고 한다.

역사

1/3–2/3 추측은 키슬리친(1968년)에 의해 공식화되었고, 이후 마이클 프레드먼과[4] 네이티 리니얼(1984년)에 의해 독립적으로 이루어졌다.[3] 그것은 오더 저널의 창간에서 풀리지 않는 특색있는 문제들로 나열되었고, 여전히 풀리지 않고 있다;[3] 브라이트웰, 펠스너 & 트로터(1995)는 이것을 "양념의 결합 이론에서 가장 흥미로운 문제들 중 하나"라고 부른다.

그 추측에 대한 조사는 브라이트웰(1999년)이 한다.

부분 결과

그 1/3–2/3 추측 일부 명령의 높이 two,[6]부분 명령의 폭 two,[5]부분 수주액에 있는 각 요소에 대부분의 6others,[8]직병렬 부분 orders,[9]semiorders 것에 비할 바 아니다 대부분에서 11명의 elements,[7]부분적 주문과 함께 부분적 주문과 특수한 클래스에 대한 진정한 것으로 알려져 있다.[10]과 polytrees.[11] n이 무한대로 가는 한계에서 1/3–2/3 추측에 따르는 n-element 부분 명령의 비율은 100%에 근접한다.[7]

브라이트웰, 펠스너 & 트로터(1995)는 총계가 아닌 유한 부분 순서 P에 대해 Δ(P) 1/2 - √5/10 ≈ 0.276임을 증명했다. 그들의 결과는 같은 유형의 이전의 약한 한계를 개선한다.[12] 그들은 Δ(P)의 확률론적 해석을 사용하여 Δ(P)의 정의를 특정 무한 부분 순서로 확장한다. 그러한 맥락에서 Δ(P) = 1/2 - ∆5/10의 무한 부분 순서가 존재한다는 점에서 이들의 한계가 최적임을 보여준다.

적용들

Kahn & Saks(1984)는 이 문제에 대해 다음과 같은 적용을 제안하였다: 어떤 사람이 완전히 주문된 집합 X를 비교하기를 원한다고 가정하자. X에 대한 일부 주문 정보가 이미 부분 주문의 형태로 알려져 있다. 최악의 경우, 요소의 쌍 x와 y 사이의 각 추가 비교는 비교 결과와 가능한 한 많은 선형 확장을 남기는 방식으로 비교를 해결함으로써 가능한 한 적은 정보를 산출할 수 있다. 1/3–2/3 추측에 따르면 각 단계에서 선형 확장의 나머지 수를 2/3 인수로 줄이는 비교를 선택할 수 있다. 따라서 초기 정보에 의해 주어진 부분 순서의 E 선형 확장이 있는 경우, 정렬 문제는 대부분의3/2 logE 추가 비교에서 완료될 수 있다.

그러나 이 분석은 비교할 최적 쌍 x와 y를 선택하는 복잡성을 무시한다. 또한 정렬 알고리즘의 각 단계에서 이러한 최악의 경우 동작이 발생할 수 없을 수 있기 때문에 이 분석이 제시하는 것보다 더 나은 수의 비교를 사용하여 부분 순서를 정렬하는 것이 가능할 수 있다. 이 방향에서 φ은 황금비를 나타내는 logEφ 비교만으로도 충분할 것으로 추측되어 왔다.[7]

Fredman(1976년)은 X의 정렬 순서가 X의 순열 S에 있는 것으로 알려졌을 때 집합 X를 정렬하는 문제와 밀접하게 관련된 분류 문제를 검토한다. 여기서 S는 반드시 부분 순서의 선형 확장 집합으로 생성되는 것은 아니다. 이러한 추가된 일반성에도 불구하고, Fredman은 빅 O 표기법으로 표현된2 로그 S + O( X ) 비교를 사용하여 X를 정렬할 수 있음을 보여준다. 이 같은 경계는 부분 주문의 경우에도 적용되며 logE2 + O(n) 비교만으로도 충분하다는 것을 보여준다.

일반화 및 관련 결과

Kahn & Saks(1984)는 w가 무한대로 되는 경향이 있는 한계에서 w의 부분 순서 폭 집합에 대한 Δ(P)의 값이 1/2로 되어야 한다고 추측했다. 특히 부분적으로만 정렬된 폭 2 집합만이 최악의 경우 값 Δ(P) = 1/3을 달성할 수 있을 것으로 예상하며, 에이그너(1985)는 이를 추측으로 명시적으로 진술했다. 폭 3의 포셋에 대해 알려진 Δ(P)의 가장 작은 값은 14/39이며,[13] 컴퓨터 검색 결과 9개 이하의 요소를 가진 폭-3 포셋에 대해서는 더 작은 값이 불가능하다는 것이 밝혀졌다.[6] 컴퓨터 검색에 근거한 또 다른 관련 추측에 의하면 1/3과 Δ(P)의 다른 가능한 값 사이에 차이가 있다고 한다. 부분 순서에 Δ(P)가 정확히 1/3이 없을 때마다 Δ(P)가 0.348843이 된다.[14]

마르친 Peczarski[7][8]가 만약 ti선형 확장 후 나는 비교에 성공해 남은 것을 나타낸다,(각 비교 가능한 네가지 결과에서)t0≥이 이 아닌 총 그 각 부분 순서에서 2년 연속 비교를 찾을 수 있는"금 파티션 추측"출연하기 위해서는 공식화했다1+t2. 이 추측은 사실이며, 이는 1/3 대 2/3 추측을 암시할 수 있다. 두 비교 중 첫 번째 비교는 나머지 비교를 최악의 1/3 대 2/3 비율로 나누는 쌍 사이의 것이어야 한다. 금 칸막이 추측은 또한 E 선형 확장이 있는 부분적인 순서가 대부분의φ logE 비교에서 정렬될 수 있음을 암시할 수 있다; 추측의 이름은 황금 비율과 이 연관성에서 유래한다.

x를 y보다 먼저 배치하는 P의 선형 확장의 비율을 계산하기 위해 유한 부분 순서 P와 한 쌍의 원소가 주어진 것은 #P-완전이다.[15]

메모들

  1. ^ 칸 & 삭스(1984); 브라이트웰, 펠스너 & 트로터(1995)
  2. ^ 아이그너(1985)
  3. ^ a b c d 브라이트웰, 펠스너 & 트로터(1995)
  4. ^ 그러나 부분적으로 주문한 데이터를 분류하는 문제와 그에 따른 1/3-2/3 추측에 프레드만(1976)이 밀접한 관련이 있음에도 불구하고, 그 논문에는 언급되지 않았다.
  5. ^ 리니얼(1984), 정리 2; 사(2021).
  6. ^ a b 트로터, 게를린&피쉬번(1992년).
  7. ^ a b c d 페차르스키(2006년).
  8. ^ a b 페차르스키(2008년).
  9. ^ 자구아(2012년).
  10. ^ 브라이트웰(1989년).
  11. ^ 자구아(2019년).
  12. ^ 칸 & 삭스(1984); 카치얀(1989); 칸 & 라이니얼(1991); 펠스너 & 트로터(1993)
  13. ^ 삭스(1985년).
  14. ^ 페차르스키(2019년).
  15. ^ Brightwell & Winkler (1991년).

참조