원시 피타고라스 세 배의 나무

수학에서, 원시 피타고라스 트리플 트리(tree)는 모든 노드의 무한 집합이 복제 없이 모든 원시 피타고라스 트리플을 제공하는 세 개의 후속 노드로 각 노드가 분기하는 데이터 트리이다.

피타고라스 트리플은 각각 두 다리와 직각 삼각형의 빗변일 수 있는 특성을 가진 3개의 양의 정수 a, b, c의 집합이다. 따라서 ${\displaystyle {a\mathrm{}}^{}}2{\displaystyle {}^{}}$ + ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {c\mathrm{}}^{}}$2 {\$display a^{2$} + b^{$2$} + b^{2}$}=c^{$2$\}\};$ 3배는 a, b, c의 최대공약수가 1인 경우에만 원시라고 한다.원시 피타고라스의 트리플 a, b, c 또한 쌍으로 이루어진 코프라임이다.모든 원시 피타고라스의 3중 집합은 뿌리 나무, 특히 3중 나무의 구조를 자연 그대로 가지고 있습니다.이것은 B에 의해 처음 발견되었다.1934년 ^[1]베르크그렌.

F. J. M. 바닝은^[2] 세 가지 매트릭스 중 하나가

${\displaystyle\array}{lcr}A="bmatrix"1&2&2&1&2&2&2&2&2&3\end{bmatrix}&B="bmatrix"1&2&2&1&2&2&2&3&C="bmatrix"-2&2&2&2&2&2&2"$

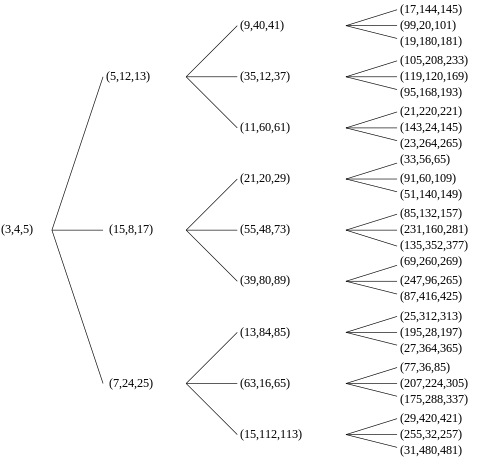
오른쪽에서 성분이 피타고라스의 트리플을 형성하는 열 벡터를 곱하면 다른 피타고라스의 트리플을 구성하는 또 다른 열 벡터가 됩니다.초기 트리플이 원시적이라면 결과도 마찬가지입니다.그래서 각각의 원시 피타고라스 세쌍은 세 명의 "아이"를 가지고 있다.모든 원시 피타고라스의 세배는 세배 (3, 4, 5)에서 이 방식으로 내려오고, 한 번 이상 나타나는 원시 세배는 없다.결과는 루트 노드에 (3, 4, 5)가 있는 무한 삼원 트리로 그래픽으로 표현될 수 있습니다(오른쪽 클래식 트리 참조).이 나무는 A씨의 논문에도 실렸다.1970년^[3] 홀, 1990년 ^[4]A.R. 캉가.2008년 V.E. Firstov는 일반적으로 이러한 삼분열 나무 3개만이 존재하며, 베르그렌과 유사한 나무를 제공하지만 초기 노드(4, 3, 5)^[5]부터 시작한다는 것을 보여주었다.

증명서

원시 피타고라스 세 배의 존재

초기 노드(3, 4, 5)에 존재하는 것과 같은 원시 피타고라스 트리플에서 시작하여 생성된 각 트리플이 피타고라스 트리플과 원시 트리플이라는 것을 보여주면 나무가 원시 피타고라스 트리플을 포함한다는 것을 귀납적으로 보여줄 수 있다.

피타고라스의 재산 보존

위의 행렬 중 하나, 예를 들어 A를 피타고라스 특성² a + b² = c를² 갖는 삼중(a, b, c)^T에 적용하여 새로운 삼중(d, e, f)^T = A(a, b, c)^T를 구하면, 이 새로운 삼중(a, b, c)도 피타고라스이다.이것은 각각 d, e, f를 a, b, c의 3개의 항의 합으로 쓰고, 각각을 제곱하여 f = d²² + e를²² 구함으로써²² 알 수 있다.이것은 A뿐만 아니라 B와 C에도 적용된다.

원시성 보존

행렬 A, B 및 C는 모두 단모듈러입니다.즉, 이들은 정수 엔트리만을 가지며 행렬식은 ±1입니다.따라서 이들의 역수 또한 단일 모듈이며 특히 정수 엔트리만 있습니다.따라서 이들 중 하나(예: A)를 원시 피타고라스 트리플(a, b, c)^T에 적용하여 또 다른 트리플(d, e,^T f)을 얻는다면, 우리는 (d,^T e, f) = A(a, b,^T c)^T = A(d, e,^T f)가⁻¹ 된다.만약 어떤 소인수가 d, e, f 중 하나(따라서 3개 모두)에 의해 공유된다면, 이 마지막 방정식에 의해 소인수는 각각 a, b, c를 나눕니다.따라서 실제로 a, b, c가 쌍으로 된 코프라임일 경우 d, e 및 f도 쌍으로 된 코프라임이어야 합니다.이것은 A뿐만 아니라 B와 C에도 적용된다.

모든 원시 피타고라스의 삼중의 존재는 정확히 한 번

나무가 모든 원시 피타고라스 세 개를 포함하지만 한 번 이상은 포함하지 않는다는 것을 보여주려면, 이러한 세 개에 대해 나무를 통해 시작점(3, 4, 5)으로 돌아가는 경로가 정확히 하나라는 것을 보여주는 것으로 충분합니다.이것은 차례로 각 행렬 역, 위의 추론 미개함과 피타 고라스 속성에 의해 유지됩니다, 가능성이 없는 트리플에(3,4,5)보다 정확히 1에서 역 것이다 전이 매트릭스의 큰 수익률을 언급하며 언급하며 A−1, B−1, C−1 임의의 원시적인 피타 고라스 수(d, e, f)에 matrices a.의 적용하여 볼 수 있 대변인.모든 양의 엔트리와 중복됩니다(및 더 작은 빗변).유도에 의해 이 새로운 유효 트리플 자체가 정확히 하나의 더 작은 유효 트리플로 이어집니다.점점 더 작은 잠재적 빗변의 수의 미세성에 의해 최종적으로 (3, 4, 5)에 도달한다.이것은 (d, e, f)가 실제로 트리에서 발생한다는 것을 증명한다. 왜냐하면 스텝을 반대로 하면 (3, 4, 5)에서 도달할 수 있기 때문이다.또한 (d, e, f)에서 (3, 4, 5)로 가는 경로가 하나밖에 없었기 때문이다.

특성.

행렬 A를 사용한 변환은 (a, b, c) = (3, 4, 5)에서 반복적으로 수행될 경우, 특징 b + 1 = c를 보존하고, 행렬 B는 (3, 4, 5)에서 시작하여 a - b = ±1을 보존하며, 행렬 C는 특징 a + 2 = c를 보존합니다.

이 트리의 기하학적 해석은 각 노드에 존재하는 엑시클을 포함한다.부모 삼각형의 세 자녀는 부모로부터 인라디아를 "상속"한다: 부모의 내시경이 다음 세대의 ^{[6]: p.7} 인라디아가 된다.예를 들어 부모(3, 4, 5)의 Excircle 반지름은 2, 3, 6입니다.이들은 세 자녀(5, 12, 13), (15, 8, 17) 및 (21, 20, 29)의 인반경이다.

만약 A 또는 C 중 하나가 초기 조건으로 사용되는 피타고라스 삼중에서 반복적으로 적용된다면, a, b, c 중 하나의 역학은 x의 역학과 같이 표현될 수 있다.

${\displaystyle x_{n+3}-3x_{n+2}+3x_{n+1}-x_{n}=0,}$

행렬의 공유 특성 방정식에 따라 패턴화됩니다.

$\displaystyle \displayda ^{3}-3\displayda ^{2}+3\displayda-1=0.,}$

만약 B가 반복적으로 적용된다면, a, b, c의 역학은 x의 역학과 같이 표현될 수 있다.

${\displaystyle x_{n+3}-5x_{n+2}-5x_{n+1}+x_{n}=0,}$

이것은 ^[7]B의 특성 방정식에 따라 패턴화되어 있다.

게다가 3차 일변량 차분 방정식의 무한은 3개의 행렬 중 하나를 임의의 수열에서 임의의 횟수로 곱함으로써 구할 수 있다.예를 들어 행렬 D = CB는 한 번에 2개의 노드(하향 후)만큼 트리 밖으로 이동하며, D의 특성 방정식은 D에 의해 형성된 비연속 트리에서 a, b 또는 c 중 하나의 3차 역학에 대한 패턴을 제공한다.

트리를 생성하는 대체 방법

이 나무의^[8] 역학에 대한 또 다른 접근법은 모든 원시 피타고라스 3배를 생성하기 위한 표준 공식에 의존합니다.

${\displaystyle a=m^{2}-n^{2},}$

${\displaystyle b=200만,}$

${\displaystyle c=m^{2}+n^{2},}$

m > n > 0, m 및 n의 동시 및 반대 패리티의 경우.쌍(m, n)은 다음 중 하나에 의해 사전 곱셈(열 벡터로 표현됨)하여 반복할 수 있습니다.

${\displaystyle {array} {lcr} {\display {bmatrix} 2&1&0\end {bmatrix}, {\display {bmatrix} 2&1&0\end {bmatrix}, & {\display {bmatrix}, {\display {bmatrix}$

각각 불평등, 동일성 및 반대되는 패리티를 보존합니다.(2,1)에서 시작하는 결과 삼원 트리는 이러한 모든 (m, n) 쌍을 정확히 한 번 포함하며, (a, b, c) 세 배로 변환하면 위에서 설명한 트리와 동일해진다.

기본 파라미터 2개를 사용하여 트리플^[9] 트리를 생성하는 또 다른 방법은 모든 기본 트리플에 대해 대체 공식을 사용합니다.

$({displaystyle a=uv,})$

${\displaystyle b=snarfrac {u^{2}-v^{2}}{2}},$

${\displaystyle c=syslogfrac {u^{2}+v^{2}}}{2}},}$

u > v > 0 및 u 및 v coprime 둘 다 홀수입니다.쌍(u, v)은 위의 2 × 2 행렬 중 하나에 의해 (열 벡터로 표현됨)을 미리 곱하여 반복할 수 있으며, 이들 3개 모두 부등식, 공명도 및 두 요소의 홀수 패리티를 보존한다.이 프로세스가 (3, 1)에서 시작되면 생성된 삼원 트리는 이러한 모든 (u, v) 쌍을 정확히 한 번 포함하며, (a, b, c) 3배로 변환하면 위에서 설명한 트리와 동일하게 됩니다.

다른 나무

또는 ^[6]Price에서 찾은 3가지 매트릭스를 사용할 수도 있습니다.이 행렬 A', B', C' 및 대응하는 선형 변환은 다음과 같습니다.

${\displaystyle{\overset{{A}의}{\mathop{\left[{\begin{매트릭스}2&, 1&, -1\\-2&, 2&, 2\\-2&, 1&, 3\end{매트릭스}}\right]}}}\left[{\begin{매트릭스}a\\b\\c\end{매트릭스}}\right]=\left[{\begin{매트릭스}a_{1}\\b_{1}\\c_{1}\end{매트릭스}}\right],\quad{\text{}}{\overset{{B}'}{\mathop{\left[{\begin{행렬}2&, 1&, 1\\2&, -2&, 2\\2&, -1&a.융점, 3\end{매트릭스}}\right 해결}}}\left -LSB-{\begin{행렬}a\b\c\end{filename}\right]=\left[{\filename}\\b_{2}\\c_{filename}\right],\filen {\text}}{\overset {C}}{\mathop {\[\filength{2-2}&1&2&1\\filengt;$

Price의 세 가지 선형 변환은

${\displaystyle{\begin{정렬}&,{\begin{행렬}+2a+b-c=a_{1}\quad&-2a+2b+2c=b_{1}\quad&-2a+b+3c=c_{1}&,\quad \to \left[{\text{}}a_{1},{\text{}}b_{1},{\text{}}c_{1}\right]\end{매트릭스}}\\&,{\begin{행렬}+2a+b+c=a_{2}\quad&+2a-2b+2c=b_{2}\quad&+2a-b+3c=c_{2}&,\quad \to \left는 경우에는{\text{}}a_{2},{\text{}}b_{2},{\text{. }}c_{2}\right 해결 \end{매트릭스}}\\&,{)begin { bigin { text } + 2a - b + 2b + 2c = b _ { 3 } = b _ { 3 } = c _ { 3 } & \ text { { } a _ { 3 } , { \ text { { } b _ { 3 } \ text { 3 } \ text { { \ } { \ }\ }\ end { }$

두 행렬 집합 각각에서 생성된 3개의 하위 행렬은 동일하지 않지만 각 집합은 모든 원시 3배를 개별적으로 생성합니다.

예를 들어 [5, 12, 13]을 부모로서 사용하면, 다음의 3명의 아이가 2 세트 됩니다.

${\displaystyle{array}{cc}&\left[5,12,13\right]&\\\\\A&B&C\left [45,28,53\right]&\left [55,48,73\right]&\end {array}\quad \quad \quad \quad \quad \quad \quad \be {array}{cc}&\left;&\left[5,12,53\right]>A'&C'\left[9,40,41\right]&\left[35,12,37\right]&\left[11,60,61\right]\end {array}}$

주 및 참고 자료

외부 링크

• 원시 피타고라스의 세 배의 밑바탕에 있는 삼진수
• 프랭크 R.베른하트, 그리고 H.리 프라이스, "피타고라스의 정원, 다시 방문", 호주 시니어 수학 저널 2012년 1월 26일 (1):29-40.[1]
• Weisstein, Eric W. "Pythagorean Triple". MathWorld.