집적 회로의 열 시뮬레이션

부품 소형화는 반도체 산업에서 항상 1차 목표였다. 왜냐하면 그것은 생산비를 절감하고 기업들이 더 작은 컴퓨터나 다른 장치들을 만들 수 있게 해주기 때문이다.그러나 소형화는 단위 면적당 소산전력을 증가시켜 집적회로 성능의 핵심 제한요소로 만들었다.온도 상승은 일반적인 반도체 거동에 영향을 미칠 수 있는 상대적으로 작은 교차점 와이어에 관련된다.게다가, 열 발생은 개폐 회로의 작동 빈도에 비례하기 때문에, 빠른 컴퓨터는 느린 컴퓨터보다 더 큰 열 발생을 가지고 있어, 칩 제조사들에게는 바람직하지 않은 효과다.이 글은 집적회로에서 열의 발생과 전도를 설명하는 물리적 개념을 요약하고, 거시적인 관점에서 열 전달을 모델링하는 수치적 방법을 제시한다.null

열 발생 및 전달

푸리에의 법칙

거시적 수준에서 푸리에의 법칙은 단위 면적당 단위 시간 당 전송되는 열과 온도 변화 사이의 관계를 다음과 같이 명시한다.

$\displaystyle q=-\kappa \nabla T}$

여기서 $\kappa {\displaystyle }$ ${\displaystyle \kappa }$은 열전도도, [W·m⁻¹ K⁻¹]이다$$.null

줄 난방

전자 시스템은 전류와 전압 신호를 기반으로 작동한다.전류는 물질과 이러한 입자(전자 또는 구멍)를 통과하는 전하 입자의 흐름으로, 열의 형태로 방출되는 에너지를 잃는 결정의 격자와 상호작용한다.Joule Heating은 집적회로에서^[1] 열 발생을 위한 주요 메커니즘이며 대부분의 경우 원하지 않는 효과다.옴질 재료의 경우 다음과 같은 형태가 있다.

${\displaystyle Q=j^{2}\rho }$

여기서 $j{\displaystyle }$ ${\displaystyle j}$은 [A·m⁻²]의 전류 밀도, $\rho {\displaystyle }$${\displaystyle }$ ${\displaystyle \rho }$은 [ ${\displaystyle \mathrm{}}${\$displaystyle {}},$Q ${\displaystyle Q}$은 [W·m⁻³]^[1]의 단위 볼륨당 발생 열이다.null

열전달 방정식

열전달 문제의 물리학의 지배 방정식은 다음과 같은 표현에 의해 공간의 열의 유동, 시간의 변동 및 동력 생성과 관련된다.

${\displaystyle \nabla \left(T\right)\nabla T\right)+g=\rho C{\frac {\partial T}{\partial t}}}}}}$

Where ${\displaystyle \kappa }$ is the thermal conductivity, ${\displaystyle \rho }$ is the density of the medium, ${\displaystyle C}$ is the specific heat, ${\displaystyle \alpha ={\frac {\kappa }{\rho C}}}$, the thermal diffusivity and ${\displaystyle g}$ is the rate of heat generation per unit 부피위의 방정식을 따르는 선원으로부터의 열 확산과 동질 매질에서의 용액은 가우스 분포를 따른다.null

열 방정식 해결 기법

키르호프 변환

$\kappa {\displaystyle }$ ${\displaystyle \kappa }$의 온도 의존성을 없애기 위해 Kirchhoff 변환을 수행할 수 있다$.$

${\displaystyle \teta =T_{s}+{\frac {1}{\cappa _{s}}\int _{T_}^{{{T_}}}}{{prac}}}}}{papa}}}}}{T_}}T}\카파(T)dT}$

여기서 ${\displaystyle {\kappa s}_{}}$ =${\displaystyle {}_{}\kappa }$(${\displaystyle {}_{}}$ ${\displaystyle s_{}}$) ${\$ 및$$ ${\displaystyle {Ts}_{}}$ ${\$는 열제거원 온도다.이 변환을 적용할 때 열 방정식은 다음과 같이 된다.

${\displaystyle \chbla ^{2}\theta +{\frac {\fract }{\cappa _{s}g={\fract \tea}{\fract t}}}}}$

여기서 $\alpha {\displaystyle }$= ${\displaystyle \frac{\kappa }{}}$ ${\displaystyle \frac{\rho }{}}$ C ${\$ {\$kappa }{\rho C}}}$은(는) 온도에 따라 달라지는 디퓨전성이라고도 한다$$.^[2]방정식을 완전히 선형화하기 위해 두 번째 변환이 사용된다.

${\displaystyle \propert_{s}\tau =\int_{0}^{t}\properties (\theta )dt}$

다음과 같은 표현을 사용함.

${\displaystyle \capa ^{2}\theta -{1}{\frac {1}{\frac {1}{s}{\fract }{\fract \tau }}}}=-{\fract \g}{\cappa _}}}}}}}}}}}}}}}}}}}$

이 방정식의 단순하고 직접적인 적용에는 근사치가 필요하다.변형된 라플라시안에서 발생하는 추가 용어들은 삭제되어 라플라시아인은 전통적인 형태로 남게 된다.^[2]null

분석 솔루션

분석 솔루션은 구체적이고 단순한 경우에 대해서만 찾을 수 있지만, 보다 복잡한 상황을 다룰 수 있는 좋은 통찰력을 준다.또한 일반 서브시스템에 대한 분석 솔루션을 결합하여 복잡한 구조물에 대한 상세한 설명을 제공할 수 있다.교수에서.라플라스 영역의 온도로 확장되는 푸리에 시리즈인 ^[2]배티의 연구는 선형화된 열 방정식의 해결책을 찾기 위해 도입된다.null

예

이 절차는 간단하지만 비교가 되지 않는 경우: GaAs로 만들어진 균일한 큐브 다이, L=300 um.상단 표면에서 온도 분포를 찾는 것이 목표다.상단 표면은 인덱스 i=1을 사용하여 더 작은 정사각형으로 축소된다.N. 그 중 하나가 근원으로 간주된다.null

라플라스 변환을 열 방정식으로 변환:

$\displaystyle \nabla ^{2}{\bar {\\세타 }-{\frac {s}{k_{s}}{\bar {\}세타 }}=0}$

여기서 $\theta {\displaystyle \stackrel{}{\mathrm{}}}$= ${\displaystyle s}$ ${\displaystyle \theta }$ -${\displaystyle \mathrm{\theta }}$( (${\displaystyle }$= 0 )${\$$세타 }}=s\theta -\theta \left(\tau =0\오른쪽)}$

기능 $Ⅱ{\displaystyle \stackrel{\text{'}}{\mathrm{}}}$의 ${\$$세타 }}$은(는) $x{\displaystyle }$ ${\displaystyle x}$ $및$ y ${\displaystyle y}$ 변수에$$ 대한 코사인 함수와 $z{\displaystyle }$ ${\displaystyle z}$ 변수에$$ 대한 쌍곡선 코사인 및 사인 측면에서 확장된다$$.다음으로, 측면 벽에 단열 경계 조건을 적용하고 하단에 고정 온도(열 싱크 온도)를 적용하여 열 임피던스 매트릭스 방정식을 도출한다.

${\displaystyle \Delta \delta _{i}=\sum _{j=1}^{{N}R_{{n}}}{{n_}}TH_{ij}}(t)P_{j}(t)}$

여기서 인덱스 $j{\displaystyle }$ ${\displaystyle j}$이(가) 전원을 설명하는 반면 $인덱스{\displaystyle }$ i ${\displaystyle i}$은 각 작은 영역을 가리킨다$$.null

파생에 대한 자세한 내용은 교수를 참조하십시오.배티의 논문.^[2]아래 그림은 치수가 300mm인 입방체 다이에 대한 이 해석 방법의 정상 상태 온도 분포를 보여준다.0.3의 정전원W는 치수 0.1L x 0.1L의 중심 표면에 적용한다.예상대로, 분포는 경계에 접근할 때 소멸되며, 최대값은 중심에 위치하며 거의 400K에 이른다.

수치해결

수치 해법은 시뮬레이션을 수행하기 위해 구조의 그물을 사용한다.가장 인기 있는 방법은 유한차 시간 영역(FDTD) 방법, 유한 요소 방법(FEM) 및 모멘트 방법(MoM)이다.

유한격차 시간영역(FDTD) 방법은 문제에 의해 정의된 특정 경계 조건뿐만 아니라 미분 방정식을 수치적으로 해결하는 데 구성되는 강력하고 대중적인 기법이다.이는 공간과 시간을 탈피하고, 유한한 차이점화 공식을 사용함으로써 이루어지기 때문에 문제의 물리학을 기술하는 부분 미분 방정식은 컴퓨터 프로그램에 의해 수치로 풀 수 있다.null

FEM은 경계 조건뿐만 아니라 미분방정식에 의해 기술된 공학 및 수학 문제를 해결하기 위해 사용되는 수치 체계이기도 하다.그것은 공간을 기본 기능이 노드나 가장자리에 할당되는 더 작은 요소로 분리한다.기본 함수는 선형 또는 상위 순서의 다항식이다.기본함수에 문제의 미분방정식과 경계조건을 적용하여 리츠 또는 갤러킨 방법을 사용하여 방정식의 시스템을 공식화한다.마지막으로 직선 방정식의 체계를 풀기 위해 직접적 또는 반복적 방법을 사용한다.^[3]열 케이스의 경우 열 속성의 비선형성 특성 때문에 FEM 방식이 더 적합하다.null

예

앞의 예는 수치적 방법으로 해결할 수 있다.이 경우 큐브는 직사각형 원소로 분해할 수 있다.기본 함수는 첫 번째 순서 근사치(선형)로 선택할 수 있다.null

${\displaystyle N_{i}^{e}={\frac {1}{1}:{2}}\xi \left(1\mp \zeta \right),\qquad i=1,4}$

${\displaystyle N_{i}^{e}={\frac {1}{1}:{2}}\eta \left(1\mp \zeta \right),\qquad i=2,5}$

${\displaystyle N_{i}^{e}={\frac {1}{1}:{2}}\좌측(1-\xi -\eta \우측)\좌측(1\mp \zeta \우측),\qquad i=3,6}$

여기서 $\zeta {\displaystyle }$= ${\displaystyle 2}$( z${\displaystyle }$- ${\displaystyle z_{}}$ ${\displaystyle {}_{}}$)${\displaystyle }$/ ${\displaystyle h_{}}$ ${\displaystyle z{}_{}}$ ${\$ ${\displaystyle z_{}}$= ${\displaystyle 0}$ ${\displaystyle z_{c}=0$이면 $\zeta {\displaystyle }$= 2 ${\displaystyle z}$/ ${\displaystyle h_{}}$ ${\$

이 기본 함수를 사용하여 Galerkin의 방법을 열전달 방정식에 적용한 후 매트릭스 방정식을 구한다.

$왼쪽[S\오른쪽]\왼쪽\{\theta \오른쪽\}+\왼쪽[R\right]{\frac {d}{dt}\왼쪽\{\theta \right\}=\{B\right\}}}}}}$

어디에,

${\displaystyle R_{ij}=\int _{v}N_{j}N_{i}dV}$

${\displaystyle S_{ij}=k\int _{v}\nabla N_{j}.\nabla N_{i}dV}$

${\displaystyle B_{i}={\frac {k}{\kappa _{s}}}\int _{\Omega _{1}}N_{i}p(x,y)d\Omega +{\frac {k}{\kappa _{s}}}\int _{v}N_{i}gdV-kT_{o}\sum _{j=0}^{N_{D}}\int _{v}\nabla N_{j}$$^{D}.\nabla N_{i}dV}$.

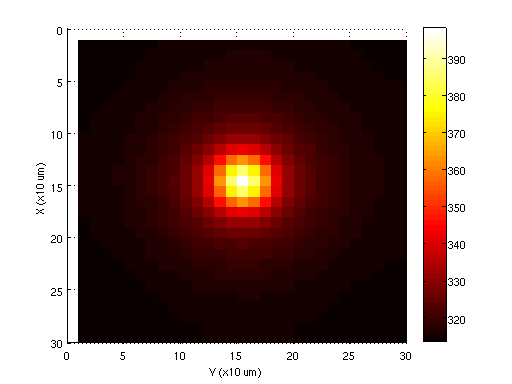
이 표현은 간단한 FEM 코드를 사용하여 평가할 수 있다.자세한 내용은 을 참조하십시오.^[3]아래 그림은 수치해결 사례에 대한 온도 분포를 보여준다.이 해결책은 분석 사례와 매우 잘 일치한다는 것을 보여주며, 그 최고치는 또한 중심에서 390K에 이른다.분포의 매끄러움 부족은 기본 함수의 첫 번째 순서 근사치에서 비롯되며, 이는 더 높은 순서 기준 함수를 사용하여 해결할 수 있다.또한, 구조물의 밀도가 더 높은 망사를 사용하여 더 나은 결과를 얻을 수 있지만, 매우 밀도가 높은 메쉬의 경우 계산 시간이 많이 증가하여 시뮬레이션을 비실용적으로 만든다.null

다음 그림은 두 방법의 시간 함수로서 피크 온도의 비교를 보여준다.시스템은 약 ${\displaystyle \mathrm{1m}}$ $[\displaystyle 1ms}$의 안정 상태에 도달한다$.$

모델오더감소

FEM 또는 FDM과 같은 수치적 방법은 앞의 절에서와 같이 행렬 방정식을 도출한다.이 방정식을 더 빨리 풀기 위해 모델 오더 감소라는 방법을 사용하여 낮은 오더의 근사치를 찾을 수 있다.이 방법은 고차원 상태 벡터가 저차원 아공간[1]에 속한다는 사실에 기초한다.null

아래 그림은 MOR 근사치의 개념을 보여준다: 매트릭스 V를 찾는 것, 시스템의 치수를 줄여 단순화된 시스템을 해결할 수 있다.null

따라서 방정식의 원래 체계는 다음과 같다.

${\displaystyle C\left\{x\right\}'+K\left\{x\right\}=F\left\{u\right\}}}}}.$

다음이 됨:

${\displaystyle V^{T}CV\left\{z\right\}'+V^{T}KV\left\{z\right\}=V^{T}F\left\{u\right\}}}}}}}}표시형 V^{T}오른쪽\}}}}}}}}$

누구의 순서가 원래보다 훨씬 낮아서 계산 비용이 훨씬 적게 든다.일단 용액을 얻으면 V로 제품을 가져가면 원래의 벡터가 발견된다.

결론

열 발생은 주로 줄 난방에 의해 발생하는데, 이러한 원치 않는 효과는 집적 회로의 성능을 제한했다.사전 설정된 기사에서는 열전도를 설명하고 열전달 문제를 해결하기 위한 분석 및 수치적 방법을 제시하였다.이러한 방법을 사용하여 입방체 다이에 대한 시간의 함수로 피크 온도뿐만 아니라 정상 상태 온도 분포를 계산했다.$입력{\displaystyle \mathrm{}\mathrm{전력}}$이 0.3 W ${\displaystyle 0.3$인 경우입방체 상단의 단일 표면 선원에 적용된 $W}($3${\displaystyle .333}$ ${\displaystyle e}$ 8 ${\displaystyle W}$/ ${\displaystyle m{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$ 3$.333e8W/m_{2$ 100 K의 순서로 최대 온도 증가를 계산했다.이 같은 온도 상승은 주변 반도체 소자의 거동에 영향을 미칠 수 있다.모빌리티와 같은 중요한 매개변수가 급격하게 변화함.그렇기 때문에 열 분산은 관련 문제로서 회로 설계를 위해 반드시 고려되어야 한다.null

참고 항목

• 집적 회로에서의 열 발생

참조