스털링 수

수학에서 스털링 숫자는 다양한 분석적 문제와 조합적 문제에서 발생한다. 그것들은 그의 저서 Methodus differentis (1730)에서 순전히 대수적 설정으로 그들을 소개한 제임스 스털링의 이름을 따서 명명되었다.^[1] 그들은 1769년 사카 마사노부에게 재발견되어 콤비네이터적인 의미를 부여받았다.^[2]

두 개의 다른 숫자의 집합은 이 이름을 가지고 있다: 첫 번째 종류의 스털링 번호와 두 번째 종류의 스털링 번호. 또한 Lah 번호는 제3종류의 스털링 번호라고도 한다. 각각의 종류는 각각의 기사에 상세하게 설명되어 있는데, 이것은 그들 사이의 관계에 대한 설명의 역할을 한다.

세 가지 유형의 공통적인 속성은 조합학에서 자주 발생하는 세 가지 다른 다항식 배열과 관련된 계수를 기술한다는 것이다. 또한, 세 가지 모두 각 부분 집합 내에서 순서를 계산하는 다른 방법을 사용하여 n개의 요소를 k개의 비어 있지 않은 하위 집합으로 분할하는 수로 정의할 수 있다.

표기법

스털링 숫자에 대한 몇 가지 다른 표기법이 사용되고 있다. 일반 (서명된) 스털링 번호에 대한 일반적인 표기법은 다음과 같다.

(\displaystyle s(n,k)\,}

k 불연속 주기가 있는 n개 원소의 순열 수를 계산하는 첫 번째 유형의 서명되지 않은 스털링 번호는 다음과 같다.

{\biggl [}{n \atop k}{\biggr ]}=c(n,k)=s(n,k)=s(-1)^{n-k(n,k)\,

두 번째 유형의 스털링 숫자의 경우, n개의 원소를 k개의 비어 있지 않은 하위 집합으로 분할하는 방법의 수를 계산한다.^[3]

\displaystyle {\biggl \{}{\\!n\! \at \at \!k\!}}{\biggr \}}=S(n,k)=S_{n}^{(k)\,}

For example, the sum ${\textstyle \sum _{k=0}^{n}\left[{n \atop k}\right]=n!}$ is the number of all permutations, while the sum ${\textstyle \sum _{k=0}^{n}\left\{{\!n\! \atop \!k\!$ $}}\right\}=B_{n}}$ 는 ${\textstyle \sum _{k=0}^{n}\left\{{\!n\! \atop \!k\!}\right\}=B_{n}}$ n번째 벨 번호다.

아브라모위츠와 스테건은 각각 첫 번째와 두 번째 스털링 번호에 대문자 ${\mathfrak {S}}$ ${\$ 를 $S$ 사용한다 ${\mathfrak {S}}$ 괄호 및 가새의 표기법은 이항계수에 비유하여 1935년 조반 카라마타에 의해 도입되었고, 이후 도널드 크누스에 의해 추진되었다. (괄호 표기법은 가우스 계수에 대한 공통 표기법과 상충된다.^[4] 스털링 번호 공식뿐만 아니라 이러한 유형의 표기법에 대한 수학적 동기는 스털링 번호와 지수 생성 함수에 대한 페이지에서 찾을 수 있다.

하강 및 상승 요인 확대

스털링 숫자는 다항식으로서 하강 및 상승 요인(Pochhammer 기호라고도 함)의 확장된 계수를 나타낸다.

즉 $(x)_{n}=x(x-1)\cdots (x-n+1)$ ( $(x)_{n}=x(x-1)\cdots (x-n+1)$ ) $(x)_{n}=x(x-1)\cdots (x-n+1)$ = x $(x)_{n}=x(x-1)\cdots (x-n+1)$ ( x $(x)_{n}=x(x-1)\cdots (x-n+1)$ - $(x)_{n}=x(x-1)\cdots (x-n+1)$ ) $(x)_{n}=x(x-1)\cdots (x-n+1)$ ( $(x)_{n}=x(x-1)\cdots (x-n+1)$ - $(x)_{n}=x(x-1)\cdots (x-n+1)$ + $(x)_{n}=x(x-1)\cdots (x-n+1)$ ) $(x)_{n}=x(x-1)\cdots (x-n+1)$ (x - n + 1) $(x)_{n}=x(x-1)\cdots (x-n+1)$ 로 정의되는 하강 요인 $(x)_{n}=x(x-1)\cdots (x-n+1)$ down interactor)은 확장인 x의 다항식이다.

(x)_{n}=\sum _{k=0}^{n}s(n,k)x^{k}}}}

(서명) 계수로 첫 번째 종류의 스털링 번호.

빈 제품이기 때문에 (x)₀ = 1이라는 점에 유의하십시오. 콤비네이터리스트들은 하강요인에 $x^{\underline {n}}$ x $x^{\underline {n}}$ $x^{\underline {n}}$ ${\$ x $^{\underline{n}}$ 라는 표기법을 사용하기도 하며, 상승요인에 $x^{\overline {n}}$ 는 x $x^{\overline {n}}$ _ $x^{\overline {n}}$ {\ $displaystyle$ x^{\ $overline{$ n}}}를 사용하기도 $x^{\overline {n}}$ 한다.(^[5]유사적으로 하강요인에 대해 많은 용도가 사용되는 Pochhammer 기호를 사용한다.)

$x^{(n)}=x(x+1)\cdots (x+n-1)$ 로 x ( n $x^{(n)}=x(x+1)\cdots (x+n-1)$ ) $x^{(n)}=x(x+1)\cdots (x+n-1)$ = $x^{(n)}=x(x+1)\cdots (x+n-1)$ ( $x^{(n)}=x(x+1)\cdots (x+n-1)$ + $x^{(n)}=x(x+1)\cdots (x+n-1)$ ) $x^{(n)}=x(x+1)\cdots (x+n-1)$ ( x + $x^{(n)}=x(x+1)\cdots (x+n-1)$ ) ⋯ ( x $x^{(n)}=x(x+1)\cdots (x+n-1)$ + $x^{(n)}=x(x+1)\cdots (x+n-1)$ ) ${\displaystyle$ x $^{(n)}=x(x+1)\cdots (x+n-1)$ 로 정의되는 상승요인은 확장이 n인 x의 다항식이다 $x^{(n)}=x(x+1)\cdots (x+n-1)$

x^{n}}=\sum _{k=0}^{n}{n}{\biggr ]}x^{k}=\sum _{k=0}-{n=0}-k(-1)^{n-k(n,k)x^{k}}}}}}}}}}

첫 번째 종류의 서명되지 않은 스털링 번호를 계수로 사용하여. $x^{(n)}=(-1)^{n}(-x)_{n}$ 팽창 중 하나는 $x^{(n)}=(-1)^{n}(-x)_{n}$ ( n $x^{(n)}=(-1)^{n}(-x)_{n}$ ) $x^{(n)}=(-1)^{n}(-x)_{n}$ = $x^{(n)}=(-1)^{n}(-x)_{n}$ ( $x^{(n)}=(-1)^{n}(-x)_{n}$ - 1 $x^{(n)}=(-1)^{n}(-x)_{n}$ ) n $x^{(n)}=(-1)^{n}(-x)_{n}$ ( $x^{(n)}=(-1)^{n}(-x)_{n}$ - $x^{(n)}=(-1)^{n}(-x)_{n}$ ) $x^{(n)}=(-1)^{n}(-x)_{n}$ ${\$ 을(를) 관찰함으로써 다른 확장 중 하나에서 도출할 수 있다 $x^{(n)}=(-1)^{n}(-x)_{n}$

두 번째 종류의 스털링 번호는 역관계를 나타낸다.

x^{n}=\sum _{k=0}^{n}S(n,k)(x)_{k}}}}

그리고

x^{n}=\sum _{k=0}^{n(1)^{n-k(n,k)x^{k}}

기본 계수의 변경으로

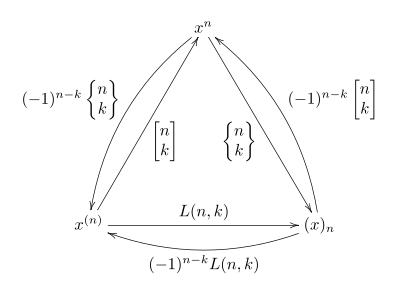
(미확정) 변수 x의 다항식 집합을 벡터 공간으로 고려하며, 세 개의 시퀀스 각각

x^{0},x^{1},x^{2,x^{3},\cHB(x)_{0},(x)_{1},\cHB \cHB(x){0},x^{(1)},x^{(2),\cHB

기초가 된다. That is, every polynomial in x can be written as a sum $a_{0}x^{(0)}+a_{1}x^{(1)}+\dots +a_{n}x^{(n)}$ for some unique coefficients $a_{i}$ (similarly for the other two bases). 그런 다음 위의 관계는 다음과 같은 대응 도표에 요약된 바와 같이 그들 사이의 근거의 변화를 표현한다.

두 개의 하단 변경에 대한 계수는 아래 Lah 번호로 설명된다. 어떤 기준으로든 계수가 고유하기 때문에 스털링 숫자를 다른 기준, 즉 위에서와 같이 하강 및 상승 요인들과 $x^{n}$ $x^{n}$ 된 x $x^{n}$ ${\$ x $^{n}$ 과 관련된 고유 번호로 정의하면 된다.

하강 요인에는 이항 ${\textstyle {\binom {x}{k}}=(x)_{k}/k!}$ 와 동일한 다항식이 정의된다. ( x k ${\textstyle {\binom {x}{k}}=(x)_{k}/k!}$ ) ${\textstyle {\binom {x}{k}}=(x)_{k}/k!}$ = ( ${\textstyle {\binom {x}{k}}=(x)_{k}/k!}$ ) ${\textstyle {\binom {x}{k}}=(x)_{k}/k!}$ k ${\textstyle {\binom {x}{k}}=(x)_{k}/k!}$ $textstyle {\binom {x}{k}}=(x)_{k}/k!}$ . The changes between the standard basis $\textstyle x^{0},x^{1},x^{2},\dots$ and the basis ${\textstyle {\binom {x}{0}},{\binom {x}{1}},{\binom {x}{2}},\dots }$ are thus described by similar formulas:

{\

}}{\biggr \}k!

{\binom {x}{k}}\cHB {\text{and}\cHB {\binom {x}{n}=\sum _{k=0}^{n}{\frac {s(n,k)}{n!

}}}x^{k

역 행렬로

제1종과 제2종의 스털링 번호는 서로 반대되는 것으로 간주할 수 있다.

\sum_{j\geq 0}s(n,j)S(j,k)=\sum_{j\geq 0}^{n-j}{n-j}{\biggr ]}{n \biggl \{}{\\\j\j\!}}{\biggr \}=\cHB _{{11}}

그리고

\sum_{j\geq 0}S(n,j)s(j,k)=\sum_{j\geq 0(-1)^{j-k}{\biggl \{}{{}\\\n\!\atop \!j\!}}{\biggr \}{\biggl [}{j \atop k}{\biggr ]}=\biggr _{biggr}}}

여기서 $\delta _{nk}$ $\delta _{nk}$ $\delta _{nk}$ ${\$ 는 Kronecker 델타다. 이 두 관계는 행렬 역관계로 이해될 수 있다. That is, let s be the lower triangular matrix of Stirling numbers of the first kind, whose matrix elements $s_{nk}=s(n,k).\,$ The inverse of this matrix is S, the lower triangular matrix of Stirling numbers of the second kind, whose entries are ${\displaystyle S_{nk}=S$ $(n,k).}$ 상징적으로 $S_{nk}=S(n,k).$ 이것은 씌어 있다.

s^{-1}=S\,

s와 S는 무한하지만, 따라서 제품 항목 계산에는 무한 합이 포함되지만, 행렬 승수는 이들 행렬이 더 낮은 삼각형이기 때문에 합계에서 한정된 수의 항만 0이 아니기 때문에 매트릭스 승수가 작용한다.

예

낙하 요인 기준으로 다항식을 표현하는 것은 연속 정수로 평가된 다항식의 합계를 계산하는 데 유용하다. 실제로 하강 요인 합계는 단순히 또 다른 하강 요인(k k-1)으로 표현된다.

\sum _{0\leq i<n}(i)_{k}={\frac {(n)_{k+1}{k+1}:{k+1}:{k+1}1}}

이는 합계가 n보다 완전히 작은 정수 i를 초과해야 함에도 불구하고, ${\textstyle \int _{0}^{n}x^{k}dx=n^{k+1}/(k+1)}$ ∆ 0 ${\textstyle \int _{0}^{n}x^{k}dx=n^{k+1}/(k+1)}$ ${\textstyle \int _{0}^{n}x^{k}dx=n^{k+1}/(k+1)}$ x ${\textstyle \int _{0}^{n}x^{k}dx=n^{k+1}/(k+1)}$ = ${\textstyle \int _{0}^{n}x^{k}dx=n^{k+1}/(k+1)}$ k ${\textstyle \int _{0}^{n}x^{k}dx=n^{k+1}/(k+1)}$ + 1 ${\textstyle \int _{0}^{n}x^{k}dx=n^{k+1}/(k+1)}$ / ( ${\textstyle \int _{0}^{n}x^{k}dx=n^{k+1}/(k+1)}$ + ${\textstyle \int _{0}^{n}x^{k}dx=n^{k+1}/(k+1)}$ ) ${\textstyle \int _{0}^{n}x^{k}dx=n^{k+1}/(k+1)}$ 와 유사하다.

예를 들어, n(n 포함)까지의 정수의 네 번째 힘의 합은 다음과 같다.

{\displaysty}&\sum _{i=0}i^{4}=\sum _{i=0}^{n}\sum _{k=0}^{4}{}}\biggl \{}\\\\\\\\atop \!k\!}}{\biggr \}}(i)_{k}=\sum _{k=0}^{4}{\biggl \{}{\\\\n\! \atop \!}}{\biggr \}{\frac {(n+1)_{k+1}:{k+1}\{k+1}\\\[8mu]&\now ={}{\\\\\\biggl \{\\\\\\}{\\\\\\\cHBiggl \{}\{\\\\\\\\\\\pup \!1\!}}{\biggr \}{\frac {(n+1)_{22}}:{2}}+{\biggl \{}{\!4\\! \ \ \at \!}}{\biggr \}{\frac {(n+1)_{3}}{3}}+{\biggl \{}{\\!4\!\! \at \ \!}}{\biggr \}{\frac {(n+1)_{4}}{4}}{4}}}{4}}{{}\biggl \{\\\\\}\op!}}{\biggr \}{\frac {(n+1)_{5}}{5}\[8mu]&\cHB ={\frac {1}{1}{1}:{1}{1}:{2}}:(n+1)_{7}{3}{3}+{6}{4}}{4}+{\frac {1}{5}}}{5}(n+1)_{5}{5}{5}}}\end{정렬}}

여기서 스털링 번호는 그 정의에서 비어 있지 않은 라벨이 부착되지 않은 k개의 하위 집합에 대한 4개 요소의 파티션 수로 계산할 수 있다.

이와는 ${\textstyle \sum _{i=0}^{n}i^{k}}$ 으로, 표준 기준의 ${\textstyle \sum _{i=0}^{n}i^{k}}$ 합계 ${\textstyle \sum _{i=0}^{n}i^{k}}$ ${\textstyle \sum _{i=0}^{n}i^{k}}$ = 0 n ${\textstyle \sum _{i=0}^{n}i^{k}}$ k {\ $textstyle \sum _{i=0}^{n}i$ ^{k $}}}}$ 는 포크하버의 공식에 의해 주어지는데, 일반적으로는 더 복잡하다.

라수

Lah 번호 $L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}$ $L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}$ ) $L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}$ = $L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}$ ( n $L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}$ - $L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}$ $L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}$ - $L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}$ ) $L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}$ $L(n,k)={n-1 \choose k-1}{\frac {n!}{k!}}$ ${\$ \선택 $k-1{\frac {n!$ $}}{k!}}}}$ 은 $L(n,k) = {n-1 \choose k-1} \frac{n!}{k!}$ (는) 제3종 스털링 넘버라고 부르기도 한다.^[6] 관례상, $L(0,0)=1$ ( $L(0,0)=1$ $L(0,0)=1$ ) = $L(0,0)=1$ {\ $displaystyle$ L( $0,0)=1$ }, $L(n,k)=0$ ( $n,$ ) $L(n,k)=0$ = $n>k$ > $n>k$ ${\$ $displaystyle$ $n$ $>k$ $k=0<n$ k = $k=0<n$ 0 < $k=0<n$ > ${\displaystyle k=0<n$

이 숫자는 감소하는 요인들을 증가하는 요인들과 그 반대로 표현되는 계수들이다.

x^{(n)}=\sum _{k=0}^{n}L(n,k)(x)_{k}\quad

and

\quad (x)_{n}=\sum _{k=0}^{n}(-1)^{n-k}L(n,k)x^{(k)}.

As above, this means they express the change of basis between the bases $(x)_{0},(x)_{1},(x)_{2},\cdots$ and $x^{(0)},x^{(1)},x^{(2)},\cdots$ , completing the diagram. 특히 하나의 공식은 다른 공식의 역행이므로 다음과 같다.

\sum _{j}L(n,j)\cdot(-1)^{j-k(j,k)=\delta _{nk}.

마찬가지로 x ( $x^{n}$ $){\$ 에서 $x^{{(n)}}$ $x^{n}$ ${\$ $displaystyle x^{n$ $(x)_{n}$ 로 $x^{n}$ 기본이 변경된 경우 $x^{n}$ x $x^{(n)}$ ( $x^{(n)}$ ${\$ $displaystyle x^{n}}$ 로 기본이 $x^{(n)}$ 직접 $(x)_{n}$ $x^{(n)}$ 되는 경우를 $(x)_{n}$ 예로 들 수 있다. $(x)_{n}$ ) $(x)_{n}$ ${\$ :

L(n,k)=\sum _{j}{n \atop j}{\biggr ]}{\biggl \{}{}\\biggl \{}{\\\!\atop \!}}{\biggr \}},

In terms of matrices, if $L$ denotes the matrix with entries $L_{nk}=L(n,k)$ and $L^{-}$ denotes the matrix with entries $L_{nk}^{-}=(-1)^{n-k}L(n,k)$ , then one is the inverse of the 기타: $L^{-}=L^{-1}$ - $L^{-}=L^{-1}$ = $L^{-}=L^{-1}$ - $L^{-}=L^{-1}$ ${\$ L $^{-}=L^{-1$ 마찬가지로, 첫 번째 종류의 서명되지 않은 스털링 번호의 행렬을 두 번째 종류의 스털링 번호의 행렬과 함께 구성하면 Lah 번호가 부여된다: $L=|s|\cdot S$ = ${\displaystyle L= \cdot S$

숫자 ${\textstyle \left\{{\!n\! \atop \!k\!}\right\},\left[{n \atop k}\right],L(n,k)}$ { ${\textstyle \left\{{\!n\! \atop \!k\!}\right\},\left[{n \atop k}\right],L(n,k)}$ ${\textstyle \left\{{\!n\! \atop \!k\!}\right\},\left[{n \atop k}\right],L(n,k)}$ , ${\textstyle \left\{{\!n\! \atop \!k\!}\right\},\left[{n \atop k}\right],L(n,k)}$ [ n ${\textstyle \left\{{\!n\! \atop \!k\!}\right\},\left[{n \atop k}\right],L(n,k)}$ ${\textstyle \left\{{\!n\! \atop \!k\!}\right\},\left[{n \atop k}\right],L(n,k)}$ , ${\textstyle \left\{{\!n\! \atop \!k\!}\right\},\left[{n \atop k}\right],L(n,k)}$ ( ${\textstyle \left\{{\!n\! \atop \!k\!}\right\},\left[{n \atop k}\right],L(n,k)}$ ${\textstyle \left\{{\!n\! \atop \!k\!}\right\},\left[{n \atop k}\right],L(n,k)}$ k ${\textstyle \left\{{\!n\! \atop \!k\!}\right\},\left[{n \atop k}\right],L(n,k)}$ ) ${\textstyle \left\{\\\\\put \!k\!$ $}}\오른쪽\}\왼쪽[{n \atop k}\오른쪽],$ $L(n,k)}$ 은(는) 비어 있지 않은 k개의 하위 집합에 대한 n개의 요소의 파티션 수로 정의될 수 있으며 ${\textstyle \left\{{\!n\! \atop \!k\!}\right\},\left[{n \atop k}\right],L(n,k)}$ , 각각 정렬되지 않은, 주기적인 순서 또는 선형 순서가 지정되어 있다. 특히 이는 다음과 같은 불평등을 내포하고 있다.

\displaystyle {\biggl \{}{\\!n\! \at \at \!k\!}}{\biggr \}\leq {\biggl [}{n \atop k}{\biggr ]}\leq L(n,k)}

대칭공식

아브라모위츠와 스테건은 제1종과 제2종의 스털링 숫자와 관련된 다음과 같은 대칭 공식을 제공한다.^[7]

s(n,k)=\sum _{j=0}^{n-k}-1+j \선택 n-k+j}{2n-k \선택 n-k-j}S(n-k+j,j)

그리고

S(n,k)=\sum _{j=0}^{n-k}-1+j \선택 n-k+j}{2n-k \선택 n-k-j}s(n-k+j,j)

음의 정수 값을 사용하여 숫자 스털링

스털링 숫자는 음의 적분 값으로 확장될 수 있지만, 모든 저자가 같은 방식으로 그렇게 하는 것은 아니다.^[8]^[9]^[10] 어떤 접근법을 취하든, 스털링의 1종과 2종의 숫자는 다음과 같은 관계에 의해 연관되어 있다는 것을 주목할 필요가 있다.

{\biggl [}{n \atop k}{\biggr ]}={\biggl \{}{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\}}{\biggr \}\cHB{\text{and}}\biggl \{}{\\n\! \otop \!}}{\biggr \}}={\biggl [}{-k \atop -n}{\biggr ]}}}

n과 k가 음이 아닌 정수일 때 $\left[{-n \atop -k}\right]$ - $\left[{-n \atop -k}\right]$ - $\left[{-n \atop -k}\right]$ $\left[{-n \atop -k}\right]$ ${\$ 에 대한 다음 표를 참조하십시오 $\left[{-n \atop -k}\right]$

k n	−1	−2	−3	−4	−5
−1	1	1	1	1	1
−2	0	1	3	7	15
−3	0	0	1	6	25
−4	0	0	0	1	10
−5	0	0	0	0	1

Donald^[10] Knuth는 모든 정수에 대해 반복 관계를 확장함으로써 더 일반적인 스털링 숫자를 정의했다. 이 ${\textstyle \left[{n \atop k}\right]}$ 접근법에서는 ${\textstyle \left[{n \atop k}\right]}$ [ ${\textstyle \left[{n \atop k}\right]}$ ${\textstyle \left[{n \atop k}\right]}$ ${\textstyle \left[{n \atop k}\right]}$ ${\$ k $}\right]$ 및 ${\textstyle \left\{{\!n\! \atop \!k\!}\right\}}$ { ${\textstyle \left\{{\!n\! \atop \!k\!}\right\}}$ ${\textstyle \left\{{\!n\! \atop \!k\!}\right\}}$ {n } ${\$ $}}\right\}$ 은(는) n이 음이고 k가 음이 아니면 0이고, n이 음이고, k가 음이면 0이고 ${\textstyle \left\{{\!n\! \atop \!k\!}\right\}}$ , 따라서 n과 k가 음수라면, 우리는 어떤 정수인 n과 k에 대해서도,

{\biggl [}{n \atop k}{\biggr ]}={\biggl \{}{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\}}{\biggr \}\cHB{\text{and}}\biggl \{}{\\n\! \otop \!}}{\biggr \}}={\biggl [}{-k \atop -n}{\biggr ]}.

반면에, n과 k의 양의 정수에 대해, 데이비드 브랜슨은^[9] ${\textstyle \left[{-n \atop -k}\right]\!,}$ [ ${\textstyle \left[{-n \atop -k}\right]\!,}$ - n ${\textstyle \left[{-n \atop -k}\right]\!,}$ - ${\textstyle \left[{-n \atop -k}\right]\!,}$ ${\textstyle \left[{-n \atop -k}\right]\!,}$ , ${\textstyle \$ $left$ $[{-n \atop -k}\right]\,}$ ${\textstyle \left\{{\!-n\! \atop \!-k\!}\right\}\!,}$ { ${\textstyle \left\{{\!-n\! \atop \!-k\!}\right\}\!,}$ - ${\textstyle \left\{{\!-n\! \atop \!-k\!}\right\}\!,}$ - ${\textstyle \left\{{\!-n\! \atop \!-k\!}\right\}\!,}$ ${\textstyle \left\{{\!-n\! \atop \!-k\!}\right\}\!,}$ ${\textstyle$ \ $\{\\!-n\!$ \! $\atop$ \!- $k\!$ $}\\\\,}$ ${\textstyle \left[{-n \atop k}\right]\!,}$ [ ${\textstyle \left[{-n \atop k}\right]\!,}$ - ${\textstyle \left[{-n \atop k}\right]\!,}$ ${\textstyle \left[{-n \atop k}\right]\!,}$ ${\textstyle \left[{-n \atop$ k $}\right]\,},$ ${\textstyle \left\{{\!-n\! \atop \!k\!}\right\}}$ { ${\textstyle \left\{{\!-n\! \atop \!k\!}\right\}}$ - ${\textstyle \left\{{\!-n\! \atop \!k\!}\right\}}$ ${\textstyle \left\{{\!-n\! \atop \!k\!}\right\}}$ ${\$ $}}\right$ ${\textstyle \left[{n \atop -k}\right]}$ [ ${\textstyle \left[{n \atop -k}\right]}$ ${\textstyle \left[{n \atop -k}\right]}$ k ${\textstyle \left[{n \atop -k}\right]}$ ] {\ $textstyle \left[{n$ \ $atop$ -k $}\right$ ${\textstyle \left\{{\!n\! \atop \!-k\!}\right\}}$ 또는 { ${\textstyle \left\{{\!n\! \atop \!-k\!}\right\}}$ - k ${\textstyle \left[{n \atop -k}\right]}$ ${\textstyle \left\{{\!n\! \atop \!-k\!}\right\}}$ {\ $textstyle \{\\\n\! \atop$ \!- $k\!$ $}}\right\}}.$ 이 접근법에서는 제1종류의 스털링 숫자의 재발관계의 확장이 다음과 같다.

{\

}}}\sum _{i=1}^{n}{\frac {(-1)^{i+1}:{i^{k}}{\binom {n}{i

예를 들어 ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ [ ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ - 5 ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ = 1 ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ ( 5 ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ - ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ k ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ + ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ 3 ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ - ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ 4 ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ + 1 ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ ) ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ . ${\textstyle \left[{-5 \atop k}\right]={\frac{120}}}}}{\bigl (}{5-{\frac {10}{$ 2}{2}{ $2$ }{2}}}{2}}{2}}}}}}}}}}}}}}{2}{2}}{2}}}}}}}}}}}}}} $^{k}}+{\frac {10}{3$ $^{k}}-{\frac {5}{4^{k}}+{\frac {1}{5^{k}}{\Bigr )}}}$ ${\textstyle \left[{-5 \atop k}\right]={\frac {1}{120}}{\Bigl (}5-{\frac {10}{2^{k}}}+{\frac {10}{3^{k}}}-{\frac {5}{4^{k}}}+{\frac {1}{5^{k}}}{\Bigr )}.}$ 이 경우 ${\textstyle \left[{-n \atop k}\right]}$ [ ${\textstyle \left[{-n \atop k}\right]}$ - n ${\textstyle \left[{-n \atop k}\right]}$ ${\textstyle \left[{-n \atop k}\right]}$ ${\$ 의 값 표로 이어진다 ${\textstyle \left[{-n \atop k}\right]}$

k n	0	1	2	3	4
−1	1	1	1	1	1
−2	${\tfrac {-1}{2}}:$	${\tfrac {-3}{4}$	${\tfrac {-7}{8}$	${\tfrac {-15}{16}$	${\tfrac {-31}{32}$
−3	${\tfrac {1}{6}$	${\tfrac {11}{36}$	${\tfrac {85}{216}$	${\tfrac {575}{1296}$	${\tfrac {3661}{7776}$
−4	${\tfrac {-1}{24}$	${\tfrac {-25}{288}$	${\tfrac {-415}{3456}$	${\tfrac {-5845}{41472}$	${\tfrac {-76111}{497664}$
−5	${\tfrac {1}{120}$	${\tfrac {137}{118}$	${\tfrac {12019}{432000}$	${\tfrac {874853}{25920000}$	${\tfrac {58067611}{1555200000}}$

이 경우 ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop -k}\right]=B_{k}}$ = ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop -k}\right]=B_{k}}$ - 1 - ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop -k}\right]=B_{k}}$ [ ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop -k}\right]=B_{k}}$ - n ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop -k}\right]=B_{k}}$ - ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop -k}\right]=B_{k}}$ ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop -k}\right]=B_{k}}$ = ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop -k}\right]=B_{k}}$ k ${\$ \sum $_{n=-1}^{-\infit }\좌측[{-n$ \n \ $atop -k}\right]=$ $B_{k}$ ${k}$ 여기서 ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop -k}\right]=B_{k}}$ $B_{k}$ k ${\$ 는 벨 번호로 $B_{k}$ , 음의 벨 번호를 ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop k}\right]=B_{-k}}$ n ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop k}\right]=B_{-k}}$ = ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop k}\right]=B_{-k}}$ - 1 - ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop k}\right]=B_{-k}}$ [ ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop k}\right]=B_{-k}}$ - n ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop k}\right]=B_{-k}}$ ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop k}\right]=B_{-k}}$ = ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop k}\right]=B_{-k}}$ - ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop k}\right]=B_{-k}}$ ${\$ n=\ $infty }\{-n \n$ \ $atop k}=$ ]로 정의할 수 있다. $B_{-k}}$ 을 ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop k}\right]=B_{-k}}$ 를) 예로 들면 ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop 2}\right]=B_{-2}=0.421773\ldots }$ = ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop 2}\right]=B_{-2}=0.421773\ldots }$ - 1 - ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop 2}\right]=B_{-2}=0.421773\ldots }$ [ ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop 2}\right]=B_{-2}=0.421773\ldots }$ - ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop 2}\right]=B_{-2}=0.421773\ldots }$ ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop 2}\right]=B_{-2}=0.421773\ldots }$ = ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop 2}\right]=B_{-2}=0.421773\ldots }$ - ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop 2}\right]=B_{-2}=0.421773\ldots }$ = ${\textstyle \sum _{n=-1}^{-\infty }\left[{-n \atop 2}\right]=B_{-2}=0.421773\ldots }$ … ${\textstyle \sum \{n=-1}^{-\infty }\{-n \atop$ 2 $}\오른쪽]=$ 이 생성된다. $B_{-2}=0.421773\ldots }$ .

참고 항목

인용구

^ 만수르 & 쇼크 2015, 페이지 5.
^ 만수르 & 쇼크 2015, 페이지 4.
^ Ronald L. Graham, Donald E. Knuth, Oren Patashnik(1988) 콘크리트 수학, Addison-Wesley, Reading MA. ISBN0-201-14236-8, 페이지 244.
^ 도널드 크누스
^ Aigner, Martin (2007). "Section 1.2 - Subsets and Binomial Coefficients". A Course In Enumeration. Springer. pp. 561. ISBN 978-3-540-39032-9.
^ Sándor, Jozsef; Crstici, Borislav (2004). Handbook of Number Theory II. Kluwer Academic Publishers. p. 464. ISBN 9781402025464.
^ Goldberg, K.; Newman, M; Haynsworth, E. (1972), "Stirling Numbers of the First Kind, Stirling Numbers of the Second Kind", in Abramowitz, Milton; Stegun, Irene A. (eds.), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 10th printing, New York: Dover, pp. 824–825
^ Loeb, Daniel E. (1992) [Received 3 Nov 1989]. "A generalization of the Stirling numbers". Discrete Mathematics. 103 (3): 259–269. doi:10.1016/0012-365X(92)90318-A.
^ ^a ^b Branson, David (August 1994). "An extension of Stirling numbers" (PDF). The Fibonacci Quarterly. Retrieved Dec 6, 2017.
^ ^a ^b D.E. Knuth, 1992.

참조

Rosen, Kenneth H., ed. (2018), Handbook of Discrete and Combinatorial Mathematics, CRC Press, ISBN 978-1-5848-8780-5
Mansour, Toufik; Schork, Mathias (2015), Commutation Relations, Normal Ordering, and Stirling Numbers, CRC Press, ISBN 978-1-4665-7989-7

추가 읽기

Adamchik, Victor (1997). "On Stirling Numbers and Euler Sums" (PDF). Journal of Computational and Applied Mathematics. 79: 119–130. doi:10.1016/s0377-0427(96)00167-7.
Benjamin, Arthur T.; Preston, Gregory O.; Quinn, Jennifer J. (2002). "A Stirling Encounter with Harmonic Numbers" (PDF). Mathematics Magazine. 75 (2): 95–103. CiteSeerX 10.1.1.383.722. doi:10.2307/3219141. JSTOR 3219141.
Boyadzhiev, Khristo N. (2012). "Close encounters with the Stirling numbers of the second kind" (PDF). Mathematics Magazine. 85 (4): 252–266. arXiv:1806.09468. doi:10.4169/math.mag.85.4.252.
Comtet, Louis (1970). "Valeur de s(n, k)". Analyse Combinatoire, Tome Second (in French): 51.
Comtet, Louis (1974). Advanced Combinatorics: The Art of Finite and Infinite Expansions. Dordrecht-Holland/Boston-U.S.A.: Reidel Publishing Company.
Hsien-Kuei Hwang (1995). "Asymptotic Expansions for the Stirling Numbers of the First Kind". Journal of Combinatorial Theory, Series A. 71 (2): 343–351. doi:10.1016/0097-3165(95)90010-1.
Knuth, D.E. (1992), "Two notes on notation", Amer. Math. Monthly, 99 (5): 403–422, arXiv:math/9205211, doi:10.2307/2325085, JSTOR 2325085
Miksa, Francis L. (January 1956). "Stirling numbers of the first kind: 27 leaves reproduced from typewritten manuscript on deposit in the UMT File". Mathematical Tables and Other Aids to Computation: Reviews and Descriptions of Tables and Books. 10 (53): 37–38. JSTOR 2002617.
Miksa, Francis L. (1972) [1964]. "Combinatorial Analysis, Table 24.4, Stirling Numbers of the Second Kind". In Abramowitz, Milton; Stegun, Irene A. (eds.). Handbook of Mathematical Functions (with Formulas, Graphs and Mathematical Tables). 55. U.S. Dept. of Commerce, National Bureau of Standards, Applied Math. p. 835.
Mitrinović, Dragoslav S. (1959). "Sur les nombres de Stirling de première espèce et les polynômes de Stirling" (PDF). Publications de la Faculté d'Electrotechnique de l'Université de Belgrade, Série Mathématiques et Physique (in French) (23): 1–20. ISSN 0522-8441.
O'Connor, John J.; Robertson, Edmund F. (September 1998). "James Stirling (1692–1770)".
Sixdeniers, J. M.; Penson, K. A.; Solomon, A. I. (2001). "Extended Bell and Stirling Numbers From Hypergeometric Exponentiation" (PDF). Journal of Integer Sequences. 4: 01.1.4.
Spivey, Michael Z. (2007). "Combinatorial sums and finite differences". Discrete Math. 307 (24). pp. 3130–3146. doi:10.1016/j.disc.2007.03.052.
Sloane, N. J. A. (ed.). "Sequence A008275 (Stirling numbers of first kind)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
Sloane, N. J. A. (ed.). "Sequence A008277 (Stirling numbers of 2nd kind)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.

[FOOTNOTEMansourSchork20155-1] 만수르 & 쇼크 2015, 페이지 5.

[FOOTNOTEMansourSchork20154-2] 만수르 & 쇼크 2015, 페이지 4.

[3] Ronald L. Graham, Donald E. Knuth, Oren Patashnik(1988) 콘크리트 수학, Addison-Wesley, Reading MA. ISBN0-201-14236-8, 페이지 244.

[4] 도널드 크누스

[5] Aigner, Martin (2007). "Section 1.2 - Subsets and Binomial Coefficients". A Course In Enumeration. Springer. pp. 561. ISBN 978-3-540-39032-9.

[6] Sándor, Jozsef; Crstici, Borislav (2004). Handbook of Number Theory II. Kluwer Academic Publishers. p. 464. ISBN 9781402025464.

[7] Goldberg, K.; Newman, M; Haynsworth, E. (1972), "Stirling Numbers of the First Kind, Stirling Numbers of the Second Kind", in Abramowitz, Milton; Stegun, Irene A. (eds.), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 10th printing, New York: Dover, pp. 824–825

[Loeb-8] Loeb, Daniel E. (1992) [Received 3 Nov 1989]. "A generalization of the Stirling numbers". Discrete Mathematics. 103 (3): 259–269. doi:10.1016/0012-365X(92)90318-A.

[:0-9] Branson, David (August 1994). "An extension of Stirling numbers" (PDF). The Fibonacci Quarterly. Retrieved Dec 6, 2017.

[:1-10] D.E. Knuth, 1992.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

Search