반복 스텐실 루프

7점짜리 3D 폰 노이만 스타일 스텐실 모양입니다.

ISL(Repeative Stencil ^[2]Loops)은 스텐실이라고 불리는 고정 패턴에 따라 배열 요소를 업데이트하는 수치 데이터 처리^[1] 솔루션의 클래스입니다.그것들은 컴퓨터 시뮬레이션에서 가장 흔하게 발견된다. 예를 들어, 과학 및 엔지니어링 애플리케이션의 맥락에서 계산 유체 역학에 관한 것이다.다른 주목할 만한 예로는 편미분 방정식,^[1] 야코비 커널, 가우스-세이델 방법,^[2] 화상 처리^[1] 및 셀 오토마타가 ^[3]있다.배열의 일반 구조는 유한 요소 방법과 같은 다른 모델링 방법과는 다른 스텐실 기술을 설정합니다.정규 그리드에서 동작하는 대부분의 유한 차분 코드는 ISL로 공식화할 수 있습니다.

정의.

ISL은 특정 ^[2]어레이를 통해 일련의 스위프(타임 스텝이라고 불립니다)를 실행합니다.일반적으로 이것은 2차원 또는 3차원 정규 ^[3]그리드입니다.배열의 요소는 셀이라고 하는 경우가 많습니다.각 시간 단계에서 모든 배열 요소가 업데이트됩니다.^[2]인접한 배열 요소를 고정 패턴(스텐실)으로 사용하여 각 셀의 새 값이 계산됩니다.대부분의 경우 경계 값은 변경되지 않은 상태로 유지되지만, 일부 경우(예: LBM 코드)는 계산 중에 조정해야 한다.각 요소에 대해 스텐실이 동일하므로 데이터 액세스 패턴이 ^[4]반복됩니다.

보다 형식적으로 ISL을 $(I,S,S_{0},s,T)$ 의 $(I,S,S_{0},s,T)$ $(I,S,S_{0},s,T)$ S 0, $(I,S,S_{0},s,T)$ T $)$ 로 정의할 수 있습니다. $표시$ (^[3]I, $S, S_{0}, s, T)$ 는 $(I, S, S_0, s, T)$ 다음과 같습니다.

$I=\prod _{i=1}^{k}[0,\ldots ,n_{i}]$ $I=\prod _{i=1}^{k}[0,\ldots ,n_{i}]$ $I=\prod _{i=1}^{k}[0,\ldots ,n_{i}]$ $I=\prod _{i=1}^{k}[0,\ldots ,n_{i}]$ $I=\prod _{i=1}^{k}[0,\ldots ,n_{i}]$ $I=\prod _{i=1}^{k}[0,\ldots ,n_{i}]$ k [ $I=\prod _{i=1}^{k}[0,\ldots ,n_{i}]$ , $I=\prod _{i=1}^{k}[0,\ldots ,n_{i}]$ , $I=\prod _{i=1}^{k}[0,\ldots ,n_{i}]$ $]$ {{ $displaystyle$ I = \ $prod _$ { i $I=\prod _{i=1}^{k}[0,\ldots ,n_{i}]$ = $I=\prod _{i=1}^{k}[0,\ldots ,n_{i}]$ 1 }^{ $k$ }[ 0 , $\ldots$ , $n _$ { i $I=\prod _{i=1}^{k}[0,\ldots ,n_{i}]$ } }는 $I=\prod _{i=1}^{k}[0,\ldots ,n_{i}]$ 인덱스 세트입니다.어레이의 토폴로지를 정의합니다.
$(\displaystyle$ S $)$ 는 $S$ (꼭 유한할 필요는 없는) 상태 집합이며, 각 셀이 주어진 시간 단계에서 취할 수 있는 상태 중 하나입니다.
$S_{0}\colon \mathbb {Z} ^{k}\to S$ 0 : $S_{0}\colon \mathbb {Z} ^{k}\to S$ k $S_{0}\colon \mathbb {Z} ^{k}\to S$ {\ $displaystyle S_{0}\colon \mathbb {Z}^{k}\to$ S $}$ 는 $S_0\colon \Z^k \to S$ 시간 0에서 시스템의 초기 상태를 정의합니다.
$s\in \prod _{i=1}^{l}\mathbb {Z} ^{k}$ $s\in \prod _{i=1}^{l}\mathbb {Z} ^{k}$ i $s\in \prod _{i=1}^{l}\mathbb {Z} ^{k}$ $s\in \prod _{i=1}^{l}\mathbb {Z} ^{k}$ l $s\in \prod _{i=1}^{l}\mathbb {Z} ^{k}$ k \ $displaystyle s$ \ $in$ _ { i $s\in \prod _{i=1}^{l}\mathbb {Z} ^{k}$ = 1 }^{ $l}\mathbb {$ Z $s\in \prod _{i=1}^{l}\mathbb {Z} ^{k}$ }^{ $k}$ 는 스텐실 그 자체이며, 실제 근방의 형상을 나타낸다.스텐실에는 디스플레이 $스타일의$ 요소가 $l$ $.$
$T\colon S^{l}\to S$ : $T\colon S^{l}\to S$ $T\colon S^{l}\to S$ $T\colon S^{l}\to S$ { $displaystyle$ T $\colon$ S $^{l}\to$ S $T\colon S^{l}\to S$ }는 $T\colon S^{l}\to S$ 셀의 인접 상태에 따라 새로운 상태를 판단하기 위해 사용되는 전이 함수입니다.

I는 k차원 정수 구간이므로 배열은 항상 유한 정규 그리드의 토폴로지를 가집니다.어레이는 시뮬레이션 공간이라고도 하며 개별 셀은 인덱스 $c\in I$ $c\in I$ I $c\in I$ \ $displaystyle$ c $\in$ I로 식별됩니다.스텐실은 l $\displaystyle$ l의 $l$ 상대좌표 $순서$ 세트입니다.이제 $각$ 셀c\ $displaystyle$ c $c$ $\$ 의 인접 $I_{c}$ 의 $I_{c}$ 을 얻을 수 있습니다.

\displaystyle I_{c}=\{j\mid\in s:j=c+x\},}

이러한 상태는 $I_{c}$ $I_{c}$ c $\$ 를 $I_{c}$ 대응하는 상태 $N_{i}(c)$ ( $N_{i}(c)$ $){displaystyle$ N_ ${i}(c$ 에 매핑함으로써 나타납니다. $N_{i}\colon I\to S^{l}$ 서 $N_{i}\colon I\to S^{l}$ $N_{i}\colon I\to S^{l}$ I $N_{i}\colon I\to S^{l}$ $N_{i}\colon I\to S^{l}$ $N_{i}\colon I\to S^{l}$ \ $N_{i}\colon I\to S^{l}$ N_ ${i}\colon$ I $\to$ S $^{l}$ 은 $N_i\colon I \to S^l$ 다음과 같이 정의됩니다.

N_{i}(c)=(s_{1},\ldots,s_{l}){\text{ with }s_{j}=S_{i}(I_{c}(j),

이는 i ${\$ $i\in \mathbb {N}$ \ $displaystyle i\in$ \ $mathbb$ {N $i\in \mathbb {N}$ 을(를) 사용하여 다음 시간 $S_{i+1}\colon \mathbb {Z} ^{k}\to S$ $S_{i+1}\colon \mathbb {Z} ^{k}\to S$ + $S_{i+1}\colon \mathbb {Z} ^{k}\to S$ : $S_{i+1}\colon \mathbb {Z} ^{k}\to S$ $S_{i+1}\colon \mathbb {Z} ^{k}\to S$ $S_{i+1}\colon \mathbb {Z} ^{k}\to S$ {\ $displaystyle$ S_ ${i+1}\colon \mathbb {Z}$ ^{ $k}\to$ S $}$ 에 $S_{i+1}\colon \Z^k \to S$ 대해 시스템 상태를 정의하는 데 필요한 전부입니다.

S_{i+1}(c)={begin{case}T(N_{i}(c), &c\in I\S_{i}(c), &c\in \mathbb {Z}^{k}\setminus I\end{case}

$S_{i}$ 조건도 설정해야 하므로 $Si는$ Z $\mathbb {Z} ^{k}$ \ $displaystyle \mathbb {Z}$ ^{ $k}$ 에 $S_{i}$ $\Z^k$ $\mathbb {Z} ^{k}$ 되어 있으며 $,$ I \ $displaystyle$ I에만 $I$ $I$ 되어 있지 않습니다.때로는 $I_{c}$ 의 $I_{c}$ (\ $style I_{$ c $I_{c}$ })를 시뮬레이션 공간의 치수에 벡터 덧셈 모듈로 정의하여 트로이덜 토폴로지를 실현할 수 있습니다.

({displaystyle I_{c}=\{j\mid\in s:j=((c+x)\mod (n_{1},\ldots,n_{k}))\}}

이는 특정 물리 모델을 단순화하는 주기적인 경계 조건 구현에 유용할 수 있습니다.

예: 2D Jacobi 반복

2D 배열에서 선택한 셀의 데이터 종속성입니다.

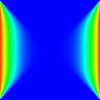
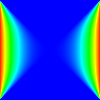
정식 정의를 설명하기 위해 2차원 Jacobi 반복을 어떻게 정의할 수 있는지 알아보겠습니다.업데이트 함수는 셀의 4개 네이버의 산술 평균을 계산합니다.이 경우 초기 해는 0으로 시작합니다.왼쪽과 오른쪽 경계는 1로 고정되고 상한과 하한은 0으로 설정됩니다.충분한 횟수 반복 후 시스템은 안장 모양으로 수렴됩니다.

디스플레이 스타일I&=[0,\ldots,99]^{2}\\S&=\mathbb {R} \\S_{0} &:\mathbb {Z}^{2}\to \mathbb {R} \\S_{0}(x,y)&=param {case}1,&x <0\0,&0\leq x <100\1,&x\geq 100\end{cases}\s&=((0,-1),(1,0),(1,0),(0,1)\\T&\colon \mathbb {R}^{4}\to \mathbb {R} \T((x_{1},x_{2},x_{3},x_{4})&=0.25\cdot(x_{1}+x_{3}+x_4}}) 정렬됨

S_{0}

S_{200}

S_{400}

S_{600}

S_{800}

S_{1000}

({

100

^{2}})

어레이에서의

100^{2}

2D Jacobi 반복

스텐실

업데이트 중에 사용되는 네이버의 모양은 응용 프로그램 자체에 따라 달라집니다.가장 일반적인 스텐실은 von Neumann 및 Moore 지역의 2D 또는 3D 버전입니다.위의 예에서는 2D von Neumann 스텐실을 사용하는 반면, LBM 코드는 일반적으로 3D 변형을 사용합니다.Conway's Game of Life는 2D Moore 지역을 사용합니다.그러나 지진파 전파용^[5] 25점 스텐실 등 다른 스텐실도 찾을 수 있습니다.

9점 2D 스텐실

5점 2D 스텐실

7점 3D 스텐실

25점 3D 스텐실

다양한 과학 분야에 사용되는 스텐실 선택입니다.

구현 문제

많은 시뮬레이션 코드가 ISL로서 자연스럽게 공식화될 수 있습니다.컴퓨팅 시간과 메모리 소비량은 어레이 요소의 수에 따라 선형적으로 증가하므로 ISL의 병렬 구현은 ^[6]연구에 있어 가장 중요합니다.계산은 (인접 셀에 따라 셀 업데이트가 이루어지기 때문에) 밀접하게 결합되어 있고, 대부분의 ISL은 메모리에 바인딩되어 있기 때문에(즉, 계산에 대한 메모리 액세스 비율이 높습니다).^[7]현재 거의 모든 병렬 아키텍처가 ISL을 ^[8]효율적으로 실행하기 위해 검토되고 있습니다.현재로서는 GPGPU가 가장 ^[9]효율적인 것으로 판명되었습니다.

라이브러리

컴퓨터 시뮬레이션에 대한 ISL의 중요성과 높은 계산 요구사항으로 인해, 스텐실 기반 계산을 수행할 때 과학자를 지원하는 재사용 가능한 라이브러리를 만드는 것을 목표로 하는 많은 노력이 있습니다.라이브러리는 병렬화에 주로 관련되어 있지만 IO, 스티어링, 체크포인트 등 다른 과제에 대처할 수도 있습니다.API에 따라 분류할 수 있습니다.

패치 기반 라이브러리

이것은 전통적인 디자인입니다.라이브러리는 업데이트를 수행하기 위해 사용자 프로그램이 액세스할 수 있는 n차원 스칼라 배열 세트를 관리합니다.라이브러리는 경계(더빙 고스트 존 또는 헤일로)의 동기화를 처리합니다.이 인터페이스의 장점은 사용자 프로그램이 어레이를 루프할 수 있기 때문에 레거시 코드를 쉽게 통합할 수 있다는 것입니다.단점은 라이브러리가 캐시 블로킹(루프^[11] 내에서 해야 하기 때문에) 또는 액셀러레이터용 API 콜의 랩핑(CUDA 또는 OpenCL 경유 등)을 처리할 수 없다는 것입니다.구현에는 물리 문제 해결 환경인 Cintens와 waLBerla가 포함됩니다.

셀 기반 라이브러리

이러한 라이브러리는 인터페이스를 단일 시뮬레이션 셀 업데이트로 이동합니다. 즉, 현재 셀과 그 인접 셀만 예를 들어 getter/setter 방법을 통해 노출됩니다.이 접근법의 장점은 라이브러리가 어떤 셀이 어떤 순서로 업데이트되는지 긴밀하게 제어할 수 있다는 것입니다.이것은 캐시 ^[9]블로킹을 구현할 뿐만 아니라 멀티코어 ^[12]및 GPU에서 동일한 코드를 실행하는 데도 유용합니다.이 방법에서는 사용자가 라이브러리와 함께 소스 코드를 다시 컴파일해야 합니다.그렇지 않으면 모든 셀 업데이트에 대해 함수 호출이 필요하며 이는 성능을 심각하게 저하시킵니다.이는 클래스 템플릿이나 메타프로그래밍과 같은 기술을 통해서만 가능하며, 이것이 이 설계가 새로운 라이브러리에서만 발견되는 이유이기도 합니다.예를 들어 Physis와 LibGeoDecomp가 있습니다.

「」를 참조해 주세요.

레퍼런스

^ ^a ^b ^c Roth, Gerald et al. (1997년) SC'97: 하이 퍼포먼스 네트워킹과 컴퓨팅의 계속.고성능 포트란의 스텐실 컴파일.
^ ^a ^b ^c ^d Sloot, Peter M.A. et al. (2002년 5월 28일) 컴퓨터 과학 – ICCS 2002: 국제 회의, 암스테르담, 네덜란드, 2002년 4월 21일 ~ 24일 제1부 절차843쪽.출판사: 스프링거. ISBN 3-540-43591-3.
^ ^a ^b ^c Fey, Dietmar et al. (2010) 그리드 컴퓨팅: Eine Basistechnologie für 계산과학.439쪽.출판사: 스프링거.ISBN 3-540-79746-7
^ 양, 로렌스 T, 궈, 민이(2005년 8월 12일) 하이 퍼포먼스 컴퓨팅: 패러다임과 인프라스트럭처221페이지.출판사: Wiley-Intercience.ISBN 0-471-65471-X
^ 미키케비치우스, 파울리우스 외(2009) CUDA를 이용한 GPU의 3D 유한차이계산 그래픽스 처리장치 범용처리에 관한 제2회 워크숍 ISBN 978-1-60558-517-8
^ Datta, Kaushik(2009) 캐시 기반 멀티코어 플랫폼용 스텐실 코드 자동 조정 2012-10-08 Wayback Machine, Ph.D.에서 아카이브된 2012-10-08.논문
^ 웰레인, G 등(2009) 멀티코어 인식 파면 병렬화에 의한 스텐실 연산을 위한 효율적인 시간 차단, 제33회 IEEE 국제 컴퓨터 소프트웨어 및 애플리케이션 컨퍼런스, COMPSAC 2009
^ 다타, 가식 등(2008) 최첨단 멀티코어 아키텍처에 관한 스텐실 컴퓨팅 최적화 및 자동 조정, SC '08 슈퍼컴퓨팅에 관한 2008 ACM/IEEE 회의의 진행
^ ^a ^b Schéfer, Andreas and Fey, Dietmar (2011) GPGPU용 고성능 스텐실 코드 알고리즘, 국제 컴퓨터 과학 회의의 진행, ICCS 2011
^ S. 도나트, J. 괴츠, C.피히팅어, KIglberger 및 U. Rüde (2010) waLBerla: 수천 개의 프로세서를 탑재한 Itanium 기반 시스템 최적화, 과학 및 엔지니어링 분야의 하이 퍼포먼스 컴퓨팅, Garching/Munich 2009
^ Nguyen, Anthony et al. (2010) 최신 CPU 및 GPU에 대한 Stencil 계산을 위한 3.5-D 블로킹 최적화, SC '10 고성능 컴퓨팅, 네트워킹, 스토리지 및 분석을 위한 2010 ACM/IEEE 국제회의 진행
^ 마루야마 나오야, 노무라 타츠오, 사토 켄토, 마츠오카 사토시(2011년) 피지스: 대규모 GPU 가속 슈퍼컴퓨터의 스텐실 연산을 위한 암묵적 병렬 프로그래밍 모델, SC '11 고성능 컴퓨팅, 네트워킹, 스토리지 및 분석을 위한 2011 ACM/IEE 국제회의 개최

외부 링크

[Roth-1] Roth, Gerald et al. (1997년) SC'97: 하이 퍼포먼스 네트워킹과 컴퓨팅의 계속.고성능 포트란의 스텐실 컴파일.

[Sloot-2] Sloot, Peter M.A. et al. (2002년 5월 28일) 컴퓨터 과학 – ICCS 2002: 국제 회의, 암스테르담, 네덜란드, 2002년 4월 21일 ~ 24일 제1부 절차843쪽.출판사: 스프링거. ISBN 3-540-43591-3.

[Fey-3] Fey, Dietmar et al. (2010) 그리드 컴퓨팅: Eine Basistechnologie für 계산과학.439쪽.출판사: 스프링거.ISBN 3-540-79746-7

[4] 양, 로렌스 T, 궈, 민이(2005년 8월 12일) 하이 퍼포먼스 컴퓨팅: 패러다임과 인프라스트럭처221페이지.출판사: Wiley-Intercience.ISBN 0-471-65471-X

[5] 미키케비치우스, 파울리우스 외(2009) CUDA를 이용한 GPU의 3D 유한차이계산 그래픽스 처리장치 범용처리에 관한 제2회 워크숍 ISBN 978-1-60558-517-8

[Datta-6] Datta, Kaushik(2009) 캐시 기반 멀티코어 플랫폼용 스텐실 코드 자동 조정 2012-10-08 Wayback Machine, Ph.D.에서 아카이브된 2012-10-08.논문

[Wellein-7] 웰레인, G 등(2009) 멀티코어 인식 파면 병렬화에 의한 스텐실 연산을 위한 효율적인 시간 차단, 제33회 IEEE 국제 컴퓨터 소프트웨어 및 애플리케이션 컨퍼런스, COMPSAC 2009

[datta2-8] 다타, 가식 등(2008) 최첨단 멀티코어 아키텍처에 관한 스텐실 컴퓨팅 최적화 및 자동 조정, SC '08 슈퍼컴퓨팅에 관한 2008 ACM/IEEE 회의의 진행

[schaefer-9] Schéfer, Andreas and Fey, Dietmar (2011) GPGPU용 고성능 스텐실 코드 알고리즘, 국제 컴퓨터 과학 회의의 진행, ICCS 2011

[walberla-10] S. 도나트, J. 괴츠, C.피히팅어, KIglberger 및 U. Rüde (2010) waLBerla: 수천 개의 프로세서를 탑재한 Itanium 기반 시스템 최적화, 과학 및 엔지니어링 분야의 하이 퍼포먼스 컴퓨팅, Garching/Munich 2009

[35dblocking-11] Nguyen, Anthony et al. (2010) 최신 CPU 및 GPU에 대한 Stencil 계산을 위한 3.5-D 블로킹 최적화, SC '10 고성능 컴퓨팅, 네트워킹, 스토리지 및 분석을 위한 2010 ACM/IEEE 국제회의 진행

[physis-12] 마루야마 나오야, 노무라 타츠오, 사토 켄토, 마츠오카 사토시(2011년) 피지스: 대규모 GPU 가속 슈퍼컴퓨터의 스텐실 연산을 위한 암묵적 병렬 프로그래밍 모델, SC '11 고성능 컴퓨팅, 네트워킹, 스토리지 및 분석을 위한 2011 ACM/IEE 국제회의 개최

[2]

[1]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[11]

[12]

Search

반복 스텐실 루프

네임스페이스

더

목차