사격법

수치해석에서는 사격방법이 경계값 문제를 초기값 문제로 축소하여 해결하는 방법이다.경계값 문제의 경계조건도 충족하는 솔루션을 찾을 때까지 다른 초기조건에 대한 초기값 문제의 해결책을 찾는 것이 포함된다.비전문가의 용어로, 다른 경계 조건을 "히트"하는 궤적을 찾을 때까지 한 경계에서 다른 방향으로 궤적을 "사격"한다.

수학적 설명

경계 값 문제를 해결하려고 한다고 가정해 보십시오.

y''=f(t)=f(t,y(t),y'(t)),\property y(t_{0}=y_{0}},\put y(t_{1})=y_{1}.

y(t;a)

(

y(t;a)

)

y(t;a)

이(가) 초기 값 문제를 해결하도록

y(t;a)

하십시오.

y"=f(t,y(t),y'(t),y(t),\property y(t)=y_{0}=y_{0},\put y'(t_{0})=a.

y(t_{1};a)=y_{1}

y(t_{1};a)=y_{1}

y(t_{1};a)=y_{1}

; a

y(t_{1};a)=y_{1}

)

y(t_{1};a)=y_{1}

= y

y(t_{1};a)=y_{1}

{\

y

(t_{1};a)=y_{1},

y(t;a)

t

y(t;a)

)

y(t;a)

도 경계값 문제의 해결책이다

y(t;a)

.

사격 방법은 원하는 경계 조건을 만족하는 $y(t;a)$ 솔루션 $y(t;a)$ ) ${\디스플레이$ 스타일 $y(t;a)}$ 을 찾을 때까지 $a$ ${\디스플레이$ 스타일 $a}$ 의 여러 가지 값에 대한 초기값 문제를 해결하는 과정이다.전형적으로, 사람들은 숫자적으로 그렇게 한다.용액은 의 루트에 해당된다.

F(a)=y(t_{1};a)-y_{1}.

사격 파라미터

a

{\displaystyle

a

}

을(를) 체계적으로 변화시키고

a

루트를 찾기 위해서는 이분법이나 뉴턴의 방법과 같은 표준적인 뿌리 찾기 알고리즘을 채용하면 된다.

$F$ $F$ 의 뿌리와 $F$ 경계 값 문제에 대한 해결책은 동일하다. $a$ 이 $F$ 가) $F$ $F$ 의 루트인 $a$ 경우 $y(t;a)$ ) $y(t;a)$ 은 경계 $y(t;a)$ 값 문제의 해결책이다.Conversely, if the boundary value problem has a solution $y(t)$ , it is also the unique solution $y(t;a)$ of the initial value problem where $a=y'(t_{0})$ , so $a$ is a root of $F$ .

어원과 직감

사격법이라는 용어는 포병에서 유래했다.촬영방법에 대한 비유는 다음과 같다.

대포를 y $y(t_{0})=y_{0}$ 0 $y(t_{0})=y_{0}$ ) = $y(t_{0})=y_{0}$ $y(t_{0})=y_{0}$ ${\$ 위치에 배치한 다음 $y(t_{0})=y_{0}$
$a=y'(t_{0})$ 의 $a=y'(t_{0})$ a $a=y'(t_{0})$ = $a=y'(t_{0})$ $a=y'(t_{0})$ ( $a=y'(t_{0})$ $a=y'(t_{0})$ ) ${\displaystyle a=y'(t_{0})$ 각도를 바꾼 다음
대포가 경계값 $y(t_{1})=y_{1}$ ( $y(t_{1})=y_{1}$ $y(t_{1})=y_{1}$ ) $y(t_{1})=y_{1}$ = $y(t_{1})=y_{1}$ $y(t_{1})=y_{1}$ ${\$ 에 도달할 때까지 발사한다 $y(t_{1})=y_{1}$

각 샷 사이에서는 이전 샷을 기준으로 대포의 방향이 조정돼 있어 샷 하나하나가 이전 샷보다 더 가까이 명중한다.원하는 경계 값을 "히트"하는 궤적은 경계 값 문제에 대한 해결책이다. 따라서 "슈팅 방법"이라는 명칭이다.

선형촬영법

f에 형식이 있을 경우 경계 값 문제는 선형이다.

f(t,y(t),y'(t)=p(t)y'+q(t)y(t)+r(t)+r(t).\,

이 경우, 경계값 문제에 대한 해결책은 대개 다음과 같이 주어진다.

y(t)=y_{(1)}(t)+{\frac {y_{1}-y_{1}-{1}-{1}(t_{1})}{y_{1}(t_{1})}{{{{1}}y_{(2)(t)}

여기서 $y_{(1)}(t)$ ( $y_{(1)}(t)$ ) $y_{(1)}(t)$ ( $y_{(1)}(t)$ ) $y_{(1)}(t)$ 은(는) 초기 값 문제에 대한 해결책이다 $y_{(1)}(t)$ .

y_{1}'=p(t)y_{(1)'(t)+q(t)y_{(1)(t)+r(t),\cHB y_{1}(t_{0})=y_{0}}}}\display y_{1}(t_{0})=0,

및 $y_{(2)}(t)$ ( $y_{(2)}(t)$ ) $y_{(2)}(t)$ ( t $y_{(2)}(t)$ ) $y_{(2)}(t)$ 은(는) 초기 값 문제에 대한 해결책이다 $y_{(2)}(t)$ .

y_{(2)"=p(t)y_{(2)y_{(2)(t)+q(t)y_{(2)}(t),\cHB y_{0}=0,\cHB y_{0}'(t_{0})=1.

이 결과가 유지되는 정확한 조건에 대한 증거를 참조하십시오.

예

표준경계값문제

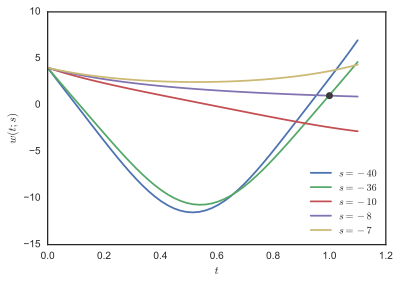
그림 1.s에 대한 궤적 w(t;s) = w'(0)가 -7, -8, -10, -36, -40과 같다.점(1,1)은 원으로 표시된다.

그림 2.함수 F = w(1;s) - 1.

경계 값 문제는 스토어 및 벌러쉬에^[1] 의해 다음과 같이 제시된다(제7.3.1절).

w"(t)"={\frac {3}{2}}w^{2},\message w (0)=4,\message w(1)=1

초기값 문제

w"(t)"={\frac {3}{2}}w^{2},\message w (0)=4,\message w'(0)=s

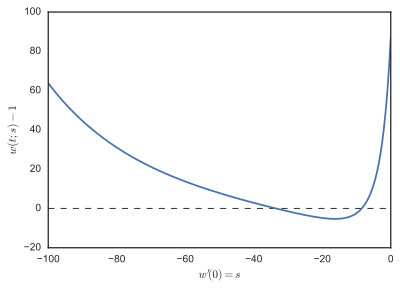
s = -1, -2, -3, ..., -100 및 F(s) = w(1;s) - 1에 대해 그림 2에서 해결되었다.F의 줄거리를 살펴보면 -8과 -36에 가까운 뿌리가 있음을 알 수 있다.w(t;s)의 일부 궤적은 그림 1에 나타나 있다.

스토어(Stoer)와 벌리르슈(Bulirsch^[1])는 두 가지 해법이 있다고 진술하고 있는데, 이는 대수학적 방법으로 찾을 수 있다.

이러한 조건은 w conditions(0) = -8 및 w′(0) = -35.9(대략)의 초기 조건에 해당한다.

고유값 문제

에너지

E_{0}=1/2

E_{0}=1/2

= 1

E_{0}=1/2

/

E_{0}=1/2

{\displaystyle E_{0}=1/2

}을

(

를) 사용하여 고조파 오실레이터의 접지 상태를 검색할 때, 슈팅 방법은 무한대로 발산하는 파장 기능을 생성한다

E_{0}=1/2

여기서 올바른 파동 기능은 뿌리가 0이고 무한대로 0으로 가야 하므로 주황색과 초록색 선 사이 어딘가에 놓여 있다.따라서 에너지는

0 .495

0.495

에서

0.495

[\displaystyle 0.500}

사이(

0.500

숫자 정확도 포함)이다.

촬영법은 고유치 문제 해결에도 활용할 수 있다.양자 고조파 오실레이터에 대한 시간 독립적인 슈뢰딩거 방정식 고려

-{\frac {1}{1}{2}}\properties _{n}"(x)+{\frac {1}{1}{2}}x^{2}\properties _{n}(x)=E_{n}\psi _{n}(x).

양자역학에서는 정규화할 수 있는 파동 기능

\psi _{n}(x)

(

\psi _{n}(x)

)

\psi _{n}(x)

및 경계

\psi _{n}(x)

조건에 따라 해당하는 에너지를 구한다.

\prow _{n}(x\오른쪽 화살표 +\fty )=\n(x\오른쪽 화살표 -\fty )=0.

n=0,1,2,\dots

문제는

n=0,1,2,\dots

=

E_{n}=n+1/2

n=0,1,2,\dots

1,

n=0,1,2,\dots

,

n=0,1,2,\dots

…

{\

displaystyle E_{n}=n+1/2}

에

E_{n}=n+1/2

대한 에너지

E_{n}=n+1/2

= n = 0, 1, 2, …[\

displaystyle n=0,1,2,\dots

n=0,1,2,\dots

을(를) 찾기 위해 분석적으로 해결할 수 있지만, 사격법에 대한 훌륭한 예시 역할도 한다.이를 적용하려면 먼저 슈뢰딩거 방정식의 몇 가지 일반 특성을 주목하십시오.

$\psi _{n}(x)$ ( $\psi _{n}(x)$ ) $\psi _{n}(x)$ 이(가) 고유 함수인 $\psi _{n}(x)$ 경우 $C$ 이 아닌 상수 C $C$ 에 $C\psi _{n}(x)$ 대한 $C\psi _{n}(x)$ $C\psi _{n}(x)$ ( $C\psi _{n}(x)$ ) ${\psi _{n}(x)$ 도 고유함수인 경우 $C$
$n$ $n$ -th $n$ 흥분 상태 $\psi _{n}(x)$ $\psi _{n}(x)$ ( $\psi _{n}(x)$ ) $\psi _{n}(x)$ 은(는 $)$ n {\ $displaystyle$ n $}$ 루트를 $n$ 가지며 $\psi _{n}(x)$ , 여기서 $\psi _{n}(x)=0$ $\psi _{n}(x)=0$ ) = $\psi _{n}(x)=0$ {\ $displaystystyle \psi _{n}(x)=$ 0}=0 $\psi _{n}(x)=0$
$n$ $n$ 의 경우에도 $n$ $n$ $n$ -th $n$ 흥분 상태 $\psi _{n}(x)=\psi _{n}(-x)$ ) = $\psi _{n}(x)=\psi _{n}(-x)$ ( $\psi _{n}(x)=\psi _{n}(-x)$ - $\psi _{n}(x)=\psi _{n}(-x)$ ) ${\displaysty \psi _{n}(x)=\psi _{n}-x}$ 는 원점에서 대칭이며 0이 아니다 $\psi _{n}(x)=\psi _{n}(-x)$ .
홀수 $n$ ${\$ $\psi _{n}(x)=-\psi _{n}(-x)$ $n$ $n$ 의 경우 $n$ ${\displaystyle$ n $\psi _{n}(x)=-\psi _{n}(-x)$ -th $n$ 흥분 상태 $\psi _{n}(x)=-\psi _{n}(-x)$ = $\psi _{n}(x)=-\psi _{n}(-x)$ ( - x $\psi _{n}(x)=-\psi _{n}(-x)$ ) ${\displaystyle \psi \n}=-\psi _{n}(-x)$ 는 대칭성이므로 원점에서 $\psi _{n}(x)=-\psi _{n}(-x)$ 0이다.

$n$ $n$ -th $n$ 흥분 상태 $\psi _{n}(x)$ ( $\psi _{n}(x)$ ) ${\displaystyle \psi _{n}(x)$ 및 $\psi _{n}(x)$ 해당 에너지 $E_{n}$ ${\$ 을 $E_{n}$ 를) 찾으려면 다음 작업을 수행하십시오.

에너지 ${\$ 를 추측해 보십시오.
슈뢰딩거 방정식을 통합한다.예를 들어, 중심 유한차이를 사용한다.
$-{\frac {1}{1}:{n2}}: {\frac {\psi _{n}^{n}^{i}+\psi _{n}^{n}^{n1}^{{\Delta x}^{2}}}+{\frac {1}{1}:{1}:{n^{{ni}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}^{2}\filename _{n}^{i}=E_{n}\psi _{n}^{i}.$
$-{\frac {1}{2}}{\frac {\psi _{n}^{i+1}-2\psi _{n}^{i}+\psi _{n}^{i-1}}{{\Delta x}^{2}}}+{\frac {1}{2}}(x^{i})^{2}\psi _{n}^{i}=E_{n}\psi _{n}^{i}.$
- $n$ ${\$ $displaystyle$ $n}$ 이 $n$ (가) 짝수인 경우 $\psi _{0}$ 0 ${\$ }=1}을 $($ 를) 임의의 숫자로 설정하고 $\psi _{0}$ (예: $\psi _{n}^{0}=1$ n $\psi _{n}^{0}=1$ = $\psi _{n}^{0}=1$ ${\displaysty$ $\psi _{n}^{0$ $}=1},$ 파형 기능은 어차피 통합 후 정규화될 수 있음) 대칭 속성을 사용하여 나머지 $\psi _{n}^{i}$ $\psi _{n}^{i}$ i { $\psi _{n}^{i}$ i를 찾으십시오 $\psi _{n}^{i}$
- If $n$ is odd, set $\psi _{n}^{0}=0$ and $\psi _{n}^{1}$ to some arbitrary number (say $\psi _{n}^{1}=1$ — the wavefunction can be normalized after integration anyway) and find all remaining ${\displ$ $aystyle \psi _{n}^{i$
$\psi _{n}$ ${\$ 의 뿌리를 세어 $\psi _{n}$ 에너지 $E_{n}$ ${\$ 에 대한 추측을 다듬는다 $E_{n}$
- $n$ $n$ 이하의 $n$ 루트가 있을 경우 추측된 에너지가 너무 낮으므로 이를 증가시키고 과정을 반복하십시오.
- 뿌리가 $n$ $n$ $n$ 개 이상일 경우 추정된 에너지가 너무 높으므로 이를 줄이고 과정을 반복하십시오.

에너지 측정은 이분법으로도 할 수 있으며, 에너지 차이가 충분히 작을 때 공정을 종료할 수 있다.그러면 그 사이에 있는 어떤 에너지도 정확한 에너지가 될 수 있다.

참고 항목

메모들

^ ^a ^b Stoer, J., Bulirsch, R. 수치 해석 소개.뉴욕: Springer-Verlag, 1980.

참조

Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Section 18.1. The Shooting Method". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.

외부 링크

ODEPAK에 대한 간략한 설명 (Netlib, LSODE 포함)
경계값 문제 해결을 위한 사격법 – Notes, PPT, Matcad, Matclab, Mathematica institutional Methods Institute [1]

[Stoer1980-1] Stoer, J., Bulirsch, R. 수치 해석 소개.뉴욕: Springer-Verlag, 1980.

[1]

Search

사격법

네임스페이스

더

목차