Quarter-wave impedance transformer

Using a transmission line as an impedance transformer.

A quarter-wave impedance transformer, often written as λ/4 impedance transformer, is a transmission line or waveguide used in electrical engineering of length one-quarter wavelength (λ), terminated with some known impedance. It presents at its input the dual of the impedance with which it is terminated.

It is a similar concept to a stub; but, whereas a stub is terminated in a short (or open) circuit and the length is chosen so as to produce the required impedance, the λ/4 transformer is the other way around; it is a pre-determined length and the termination is designed to produce the required impedance.

The relationship between the characteristic impedance, Z0, input impedance, Zin and load impedance, ZL is:

Applications

The lumped-elementlow-pass filter (top) can be converted to a design that eliminates the inductors and contains capacitors only by the use of J-inverters, resulting in a mixed lumped-element and distributed-element design.

At radio frequencies of upper VHF or higher up to microwave frequencies one quarter wavelength is conveniently short enough to incorporate the component within many products, but not so small that it cannot be manufactured using normal engineering tolerances, and it is at these frequencies where the device is most often encountered. It is especially useful for making an inductor out of a capacitor, since designers have a preference for the latter.[1]

또 다른 애플리케이션은 DC 전원을 전송 라인에 공급해야 할 때인데, 예를 들어 스위칭 트랜지스터나 변압기 다이오드와 같이 라인에 연결된 활성 소자에 전원을 공급하기 위해 필요할 수 있다. 이상적인 DC 전압 선원은 0임피던스를 가지고 있다. 즉, 단락을 나타내므로 라인을 가로질러 직접 단락을 연결하는 것은 유용하지 않다. λ/4 변압기를 통해 DC에 전원을 공급하면 단락 회로가 단선으로 변환되어 라인의 신호에 영향을 미치지 않는다.[2] 마찬가지로, 개방 회로는 단락 회로로 변환될 수 있다.[3]

이 장치는 필터의 구성요소로 사용될 수 있으며, 이 애플리케이션에서는 임피던스의 수학적 반전을 생성하기 때문에 인버터라고도 한다. 임피던스 인버터는 정류기의 역기능을 갖는 장치에 대해 파워 인버터의 더 일반적인 의미와 혼동해서는 안 된다. 인버터는 임피던스를 뒤집는 기능이 있는 회로의 종류에 대한 일반적인 용어다. 그러한 회로가 많으며 이 용어가 반드시 //4 변압기를 의미하는 것은 아니다. 인버터의 가장 일반적인 용도는 래더 네트워크와 같은 2-element-kind[4] LC 필터 설계를 1-element-kind 필터로 변환하는 것이다. 마찬가지로, 밴드패스 필터의 경우, 2-리소네이터 종류(리소네이터 및 안티리소네이터) 필터를 1-리소네이터 종류로 변환할 수 있다. 인버터는 직렬 임피던스 또는 션트 진입 여부에 따라 K인버터 또는 J인버터로[5] 분류된다.[1] λ/4 인버터를 포함하는 필터는 좁은 밴드 적용에만 적합하다. 임피던스 변압기 라인은 하나의 특정 주파수에서만 정확한 전기 길이가 λ/4이기 때문이다. 신호가 이 주파수로부터 추가될수록 임피던스 변압기는 임피던스 인버터 기능을 덜 정확하게 재현할 것이며, 원래 덩어리 요소 필터 설계의 요소 값을 덜 정확하게 나타낼 것이다.[6]

운영이론

Quarter-wave transformers are illustrated in an impedance Smith chart. Looking towards a load through a length l of lossless transmission line, the normalized impedance changes as l increases, following the blue circle. At l=λ/4, the normalized impedance is reflected about the centre of the chart.
Standing waves on a transmission line with an open-circuit load (top), and a short-circuit load (bottom). Black dots represent electrons, and arrows show the electric field. A quarter-wavelength away from the open-circuit, the current and voltage oscillations are exactly the same as at a short-circuit, and vice versa. This reflects the fact that open circuit (Z=∞) is dual to short circuit (Z=0).

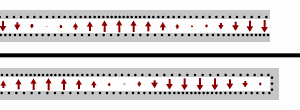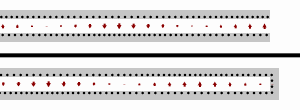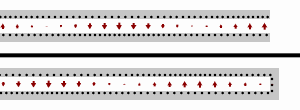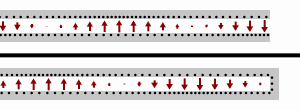
A transmission line that is terminated in some impedance, ZL, that is different from the characteristic impedance, Z0, will result in a wave being reflected from the termination back to the source. At the input to the line the reflected voltage adds to the incident voltage and the reflected current subtracts (because the wave is travelling in the opposite direction) from the incident current. The result is that the input impedance of the line (ratio of voltage to current) differs from the characteristic impedance and for a line of length l is given by;[7]

where γ is the line propagation constant.

A very short transmission line, such as those being considered here, in many situations will have no appreciable loss along the length of the line and the propagation constant can be considered to be purely imaginary phase constant, iβ and the impedance expression reduces to,[7]

Since β is the same as the angular wavenumber,

for a quarter-wavelength line,

and the impedance becomes, taking the limit as the tangent function argument approaches

which is the same as the condition for dual impedances;

Notes

  1. ^ a b Matthaei et al, pp.144-149.
  2. ^ Bhat & Koul, p.686.
  3. ^ Bhat & Koul, pp.601-602.
  4. ^ A 2-element-kind network is one consisting of only two kinds of elements, that is, LC, RC or RL circuits.
  5. ^ The K and J notation originates in archaic symbols for impedance and admittance respectively. The K is the same K that makes an appearance in the well known constant-k filter and the K parameter is defined for inverters of lumped-element design in exactly the same way as it is defined for the constant-k filter. For a λ/4 transformer the difference is moot, the same device will serve as a K-inverter with an inverter parameter of K=Z0 or equally as a J-inverter with an admittance inverter parameter of J=Y0, the characteristic admittance (=1/Z0).
  6. ^ Matthaei et al, pp.434-435.
  7. ^ a b Connor, pp.13-16.

References

  • Bharathi Bhat, Shiban K. Koul, Stripline-like transmission lines for microwave integrated circuits, New Age International, 1989 ISBN81-224-0052-3.
  • F.R. Connor, Wave Transmission, Edward Arnold Ltd., 1972 ISBN 0-7131-3278-7
  • George L. Matthaei, Leo Young and E. M. T. Jones, Microwave Filters, Impedance-Matching Networks, and Coupling Structures McGraw-Hill 1964.