볼록 세트 위의 투영

이 글은 독자들에게 혼란스럽거나 불명확할 수 있다. 기사에 대해 명확하게 설명할 수 있도록 도와주십시오. 토크 페이지에서 이에 대한 논의가 있을 수 있다.(2018년 4월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

수학에서, 때때로 교대 투영법으로 알려진 볼록 세트(POCS)에 대한 투영은 두 개의 닫힌 볼록 세트의 교차점에서 점을 찾는 방법이다.그것은 매우 간단한 알고리즘이며 여러 번 재발견되었다.^[1]가장 간단한 경우는, 세트들이 부속 공간일 때, 존 폰 노이만이 분석했다.^[2][3]집합이 부착된 공간인 경우, 교차점(교차점이 비어 있지 않은 것으로 가정)의 점으로 수렴할 뿐만 아니라 교차점에 점의 직교 투영까지 반복되기 때문에 특별한 경우.일반 폐쇄 볼록 세트의 경우 한계점이 투영일 필요는 없다.두 개의 닫힌 볼록 세트의 경우에 대한 고전적인 연구는 이테르테이트의 수렴 속도가 선형이라는 것을 보여준다.^[4][5]현재 세트가 둘 이상 있거나 세트가 볼록하지 않거나 ^[6]더 빠른 수렴 속도를 제공하는 경우를 고려하는 확장자가 있다.POCS 및 관련 방법의 분석은 알고리즘이 수렴(그리고 만일 수렴 속도를 찾는다)하고, 원점 투영으로 수렴되는지 여부를 나타내려고 한다.이 질문들은 주로 단순한 사례로 알려져 있지만, 그 연장선상에 대한 활발한 연구의 주제다.또한 Dykstra의 투영 알고리즘과 같은 알고리즘의 변형도 있다.POCS 방법의 변형, 확장 및 적용에 대한 개요는 추가 읽기 섹션의 참조를 참조하십시오. 좋은 과거 배경은 의 섹션 III에서 찾을 수 있다.^[7]

알고리즘.

POCS 알고리즘은 다음과 같은 문제를 해결한다.

${\displaystyle {\text{find}\;x\in \mathb {R} ^{n}\quad {\text{\in C\cap D}$

여기서 C와 D는 닫힌 볼록 세트다.

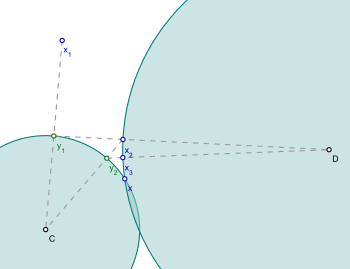
POCS 알고리즘을 사용하려면 세트 C와 D에 따로 투영하는 방법을 알아야 한다.알고리즘은 $x{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$에 대한 임의 값으로 시작한 다음$$ 시퀀스를 생성함

${\displaystyle x_{k+1}={\mathcal {P}_{C}\왼쪽({\mathcal {P}_{D}(x_{k})\오른쪽).}$

알고리즘의 단순성은 그 인기의 일부를 설명해준다.C와 D의 교차점이 비어 있지 않으면 알고리즘에 의해 생성된 시퀀스가 이 교차점의 어느 지점에 수렴된다.

Dykstra의 투영 알고리즘과 달리, 용액은 교차로 C와 D에 투영될 필요가 없다.

관련 알고리즘

평균적인 투영 방법은 상당히 비슷하다.두 개의 닫힌 볼록 세트 C와 D의 경우, 다음까지 진행한다.

${\displaystyle x_{k+1}={\frac {1}{1}:{2}}({\mathcal {P}}{C}(x_{k})+{\mathcal {P}{D}(x_{k})}}}}}}}$

그것은 오래 전부터 세계적으로 수렴된 것으로 알려져 있다.^[8]또한 이 방법은 세 개 이상의 세트로 일반화하기가 쉽다. 이 경우에 대한 몇 가지 수렴 결과가 있다.^[9]

평균 투영 방법은 표준 기법을 사용하여 교대 투영 방법으로 재구성할 수 있다.세트 고려

${\displaystyle E=\{(x,y):x\in C,\;y\in D\}$

제품 공간 $R{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ n ${\$에 정의된 다음 제품 공간에서도 다른 세트를 정의하십시오$.$

${\displaystyle F=\{(x,y):x\in \mathb {R} ^{n},\,y\in \mathb {R} ^{n},\;x=y\}.}$

따라서 $C{\displaystyle }$ ${\displaystyle \cap }$ ${\displaystyle D}$ ${\displaystyle C\cap D}$을(를) 찾는 것은$$ $E{\displaystyle }$ ${\displaystyle \cap }$ ${\displaystyle F}$ ${\displaystyle E\cap F}$을(를) 찾는 것과 같다$.$

$E{\displaystyle }$ ${\displaystyle \cap }$ ${\displaystyle F}$ ${\displaystyle E\cap F}$에서 점을 찾으려면 교대 투영 방법을 사용하십시오$.$설정된 F에${\displaystyle \mathrm{대한}\mathrm{벡터}(}$x$$$$, y ) {\$displaystyle($x,$y)}$의 투영은${\displaystyle }$(${\displaystyle x}$+ y${\displaystyle }$, ${\displaystyle x}$+ ${\displaystyle y}$)${\displaystyle }$/ ${\displaystyle 2\mathrm{}}$ ${\displaystyle (x+y,x+y)/2}$에 의해 주어진다$.$ 따라서

${\displaystyle (x_{k+1},y_{k+1}={\mathcal {P}_{F}({\mathcal {P}_{E})(x_{k},y_{k}))={\mathcal {P}_{k})={\mathcal {P}}_{F}(({\mathcal {P}}_{C}x_{k},{\mathcal {P}}_{D}y_{k}))={\frac {1}{2}}({\mathcal {P}}_{C}(x_{k})+{\mathcal {P}}_{D}(y_{k}),({\mathcal {P}}_{C}(x_{k})+{\mathcal {P}}_{D}(y_{k})).}$

Since ${\displaystyle x_{k+1}=y_{k+1}}$ and assuming ${\displaystyle x_{0}=y_{0}}$, then ${\displaystyle x_{j}=y_{j}}$ for all ${\displaystyle j\geq 0}$, and hence we can simplify the iteration to ${\displaystyle x_{k+1}=\frac{1}{2}({\mathcal{P}}_C(x_k)+{\mathcal{P}}_{}}$${\displaystyle D_{}}$( ${\displaystyle {}_{}}$ $){\displaystyle x_{k+1}={\frac {1}{1$}:{2$}}({\mathcal {P}}{C}(x_{k})+{\mathcal {P}{D}(x_{k$

참조

추가 읽기

• 2011년 책: SIAM에서 발행한 르네 에스칼란테와 마르코스 레이단(2011년)의 교차 투영법