인구비율

통계에서 일반적으로 $P$ $P$ 또는 $P$ 그리스 문자 $\pi$ $\pi$ 로 표시되는 모집단 비율은 모집단과 관련된 백분율 값을 설명하는 매개변수다 $\pi$ ^[1] 예를 들어, 2010년 미국 인구 조사에서는 미국 인구의 83.7%가 히스패닉이나 라틴계 인구가 아닌 것으로 확인되었다. .837의 가치는 인구 비율이다. 일반적으로 모집단 비율과 기타 모집단 모수는 알려져 있지 않다. 인구 모수의 실제 가치를 결정하기 위해 인구 조사를 실시할 수 있지만 비용과 시간 소비로 인해 인구 조사가 현실적이지 않은 경우가 많다.

모집단 비율은 보통 관찰 연구나 실험에서 얻은 편향되지 않은 표본 통계량을 통해 추정한다. 일례로 국가기술지식인회의는 성인 2000명을 대상으로 전국 설문조사를 실시해 경제 문맹 성인의 비율을 파악했다. 이 연구는 표본 추출한 2,000명의 성인 중 72%가 국내총생산이 무엇인지 이해하지 못했다는 것을 보여주었다.^[2] 72%의 값은 표본 비율이다. 표본 비율은 일반적으로 ${\hat {p}}$ ${\hat {p}}$ ${\$ 일부 ${\hat {p}}$ $p$ 에서는 p ${\displaystyle$ p $}$ 로 표시된다 $p$ ^[3]^[4]

수학적 정의

세트

R

R

과

R

(와) 하위 집합

S

S

의 벤 다이어그램 그림

S

R

R

에

있는

S

S

의

S

양을 측정하여 비율을 계산할 수 있다

R

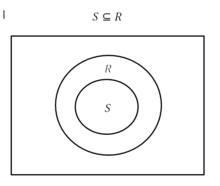
비율은 수학적으로 $집합$ R ${\displaystyle$ $S}$ 의 값에 대한 부분 $S$ 집합 $S$ ${\displaystyle$ $S}$ 의 값의 비율로 정의된다 $R$

이와 같이 인구비율은 다음과 같이 정의할 수 있다.

$P={\frac {X}{N}}$ = $P={\frac {X}{N}}$ $P={\frac {X}{N}}$ ${\$ $X$ 서 X $X$ 은 $X$ (는) 모집단의 성공 횟수, $N$ $N$ 은 $N$ 모집단의 크기)

이 수학적 정의는 표본 비율에 대한 정의를 제공하기 위해 일반화할 수 있다.

${\hat {p}}={\frac {x}{n}}$ ${\hat {p}}={\frac {x}{n}}$ = ${\hat {p}}={\frac {x}{n}}$ ${\hat {p}}={\frac {x}{n}}$ ${\$ 여기서 $x$ $x$ 은 $x$ 표본의 성공 횟수, $n$ $n$ 은 $n$ 모집단으로부터 얻은 표본 크기)^[5]^[3]

추정

추정 통계에서 연구의 주요 초점 중 하나는 매개변수의 "참" 값을 결정하는 것이다. 일반적으로, 연구 인구에 대한 인구 조사를 실시하지 않는 한, 모수에 대한 실제 값은 결코 발견되지 않을 것이다. 그러나 모수에 대한 합리적인 추정치를 얻기 위해 사용할 수 있는 통계적 방법이 있다. 이러한 방법에는 신뢰 구간과 가설 검정이 포함된다.

인구비례의 가치를 추정하는 것은 농업, 기업, 경제, 교육, 공학, 환경학, 의학, 법률, 정치학, 심리학, 사회학 분야에서 큰 시사점이 될 수 있다.

모집단 비율은 공식이 아래에 제시된 Z 간격에서 1-표본 비율이라고 알려진 신뢰 구간의 사용을 통해 추정할 수 있다.

${\hat {p}}\pm z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ (where ${\hat {p}}$ is the sample proportion, $n$ is the sample size, and $z^{*}$ is the upper ${\frac {1-C}{2}}$ ${\frac {1-C}{2}}$ 신뢰도 $C$ ${\frac {1-C}{2}}$ {\ $displaystyle {\frac {1-C}{2}}:$ 신뢰 수준에 대한 $표준$ 정규 분포의 임계값 ${\frac {1-C}{2}}$ C $C$ )

증명하다.

Z-간격에서 1-표본 비율에 대한 공식을 도출하려면 표본 비율의 표본 분포를 고려해야 한다. 이후 P의 가치{P\displaystyle}unkn은μ p^)P{\displaystyle \mu_{\hat{p}}=P 샘플 비율의 표본 분포의 평균 보통},σ p^)P(1− P)n{\displaystyle \sigma_{\hat{p}}={\sqrt{\frac{P(1-P)}{n}는 표준 편차 표시됩니다. 표시됩니다.}}}.[3].악n, 편향되지 않은 통계 ${\hat {p}}$ ${\hat {p}}$ ${\$ 이(가) $P$ $P$ 에 사용됨 ${\hat {p}}$ $P$ 평균과 표준편차는 각각 $\mu _{\hat {p}}={\hat {p}}$ $\sigma _{\hat {p}}={\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ ^ $\mu _{\hat {p}}={\hat {p}}$ = $^{\$ 과 $\sigma _{\hat {p}}={\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ $\sigma _{\hat {p}}={\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ = p $\sigma _{\hat {p}}={\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ ( $\sigma _{\hat {p}}={\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ - $\sigma _{\hat {p}}={\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ $\mu _{\hat {p}}={\hat {p}}$ $\sigma _{\hat {p}}={\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ ) $\sigma _{\hat {p}}={\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ n ${\$ 중심 한계 정리를 실행하면 표본 비율의 표본 분포는 대략 정규 분포를 따른다. 단, 표본이 상당히 크고 다듬지 않은 경우.

다음과 같은 확률을 계산합니다. P(− z∗<>p^ − Pp^(1− p^)n<>z∗)=C{P(-z^{*}<,{\frac{{\hat{p}}-P}{\sqrt{\frac{{\hat{p}}(1-{\hat{p}})\displaystyle}{n}}}}<>z^{*})=C}, 0<>C<1{\displaystyle 0<, 가정하자.C< 1}과±z∗{\displaystyle\pm z^{*}}은. 표준 임계 값

표본 비율의 표본 분포는 중앙 한계 정리 요건을 충족할 때 거의 정규 분포를 따른다.

불평등 $-z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*}$ - $-z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*}$ $-z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*}$ < $-z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*}$ $-z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*}$ - $-z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*}$ P $-z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*}$ ( $-z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*}$ - $-z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*}$ $-z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*}$ < $-z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*}$ ${\$ {{ $p}}{\p}}}{n}}}}<z^{*}}}}}$ 은 다음과 같이 대수적으로 다시 쓸 수 있다 $-z^{*}<{\frac {{\hat {p}}-P}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}}<z^{*}$ .

− z∗<>p^ − Pp^(p1− ^)n<>z∗ ⇒− z∗ p^(p1− ^)n<>p^ − P<>z∗ p^(p1− ^)n⇒− p^− z∗ p^(p1− ^)n<>− P<>− p^+z∗ p^(p1− ^)n⇒ p^. − z∗P^(p1− ^)n<>P<>p^+z∗ p^(p1− ^)n{\displaystyle -z^{*}<,{\frac{{\hat{p}}-P}{\sqrt{\frac{{\hat{p}}(1-{\hat{p}})}{n}}}}<>z^{*}\Rightarrow -z^{*}{\sqrt{\frac{{\hat{p}}(1-{\hat{p}})}{n}}}<>{\hat{p}}-P<, z^{*}{\sqrt{\frac{{\hat{p}}(1-{\hat{p}})}{n}}}\Rightarrow-.{\hat{p}}-z^{*}{\sqrt{\frac{{\hat{p}}(1-{\hat{p}})}{n}}}<>-P<, -{\hat{p}}+z^{*}{\sqrt{\frac{{\hat{p}}(1-{\hat{p}})}{n}}}\Rightarrow{\hat{p}}-z^{*}{\sqrt{\frac{{\hat{p}}(1-{\hat{p}})}{n}}}<>.P<,{\hat{p}}+z^{*}{\sqrt{\frac{{\hat{p}}(1-{\hat{p}})}{n}}}}은 대수 작업 위 해부터 확실한 C{\displaysty의 수준에서 뚜렷이 드러난다. $P$ ${\displaystyle$ ${\hat {p}}\pm z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ $}$ 이(가) ${\hat {p}}\pm z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ ${\hat {p}}\pm z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ ± z ${\hat {p}}\pm z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ ( ${\hat {p}}\pm z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ - ${\hat {p}}\pm z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ ${\hat {p}}\pm z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$ ${\$ {{ $p}}{1-{\hat{p}}}}{n}}}}}}$ 의 값 사이에 들어갈 수 있는 $P$ Le C ${\hat {p}}\pm z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}$

추론 조건

일반적으로 모집단 비율을 추정하는 데 사용되는 공식은 알려진 숫자 값의 대체를 요구한다. 그러나 통계적 추론에서 알 수 없는 모수의 추정이 정당화될 것을 요구하기 때문에 이러한 숫자 값은 공식으로 "눈으로" 대체될 수 없다. 모수의 추정이 정당화되려면 다음 세 가지 조건을 검증해야 한다.

데이터의 개별 관측치는 관심 모집단의 단순한 랜덤 표본을 통해 얻어야 한다.
데이터의 개별 관측치는 정규성을 표시해야 한다. 이는 다음과 같은 정의로 수학적으로 검증할 수 있다.
- $n$ $n$ 을(를) 지정된 랜덤 표본의 표본 크기로 하고 $n$ ${\hat {p}}$ ${\hat {p}}$ ${\$ 을(를) 표본 ${\hat {p}}$ 비율로 한다. n $n{\hat {p}}\geq 10$ $n{\hat {p}}\geq 10$ $^$ $n{\hat {p}}\geq 10$ {\ $displaystyle$ n ${\p}\geq 10}$ 및 n $n{\hat {p}}\geq 10$ $n(1-{\hat {p}})\geq 10$ - $n(1-{\hat {p}})\geq 10$ $n(1-{\hat {p}})\geq 10$ ) $n(1-{\hat {p}})\geq 10$ $n(1-{\hat {p}})\geq 10$ ${\displaystyle n(1-{\hat$ { $p})\geq 10$ 인 경우, 데이터의 개별 관측치는 정규성을 나타낸다.
데이터의 개별 관측치는 서로 독립적이어야 한다. 이는 다음과 같은 정의로 수학적으로 검증할 수 있다.
- $N$ $N$ 을(를) 관심 모집단의 크기로 하고 $N$ $n$ $n$ 을(를) 모집단의 단순 랜덤 표본의 표본 크기로 $n$ 한다. $N\geq 10n$ $N\geq 10n$ $N\geq 10n$ ${\displaystyle N\geq 10n$ 인 경우 데이터의 개별 관측치는 서로 독립적이다.

SRS, 정규성 및 독립성을 위한 조건은 대부분의 통계 교과서에서 추론 도구 상자의 조건으로 언급되기도 한다.

예

대통령 선거가 민주주의에서 열리고 있다고 가정하자. 민주주의 유권자 인구 중 유권자 400명을 무작위로 표본으로 추출한 결과 272명의 유권자가 B 후보를 지지하고 있는 것으로 나타났다. 한 정치학자는 투표인구의 몇 퍼센트가 B 후보를 지지하는지 결정하기를 원한다.

정치학자의 질문에 답하기 위해 신뢰도 95%의 Z간격에서 1표본 비율을 구성하여 B 후보를 지지하는 이 민주주의에서 적격 유권자의 인구 비율을 결정할 수 있다.

해결책

무작위 샘플에서 ${\hat {p}}={\frac {272}{400}}=0.68$ ${\hat {p}}={\frac {272}{400}}=0.68$ = ${\hat {p}}={\frac {272}{400}}=0.68$ ${\hat {p}}={\frac {272}{400}}=0.68$ = 0 ${\hat {p}}={\frac {272}{400}}=0.68$ ${\p}={\frac {272}{400}}=0.68$ 의 샘플 크기가 ${\hat {p}}={\frac {272}{400}}=0.68$ $n=400$ = $n=400$ ${\displaystyn=400}$ 인 것으로 알려져 있다 $n=400$ 신뢰 구간을 구성하기 전에 추론 조건을 검증한다.

400명의 유권자의 무작위 표본을 투표인구에서 얻은 이후, 단순 무작위 표본을 위한 조건이 충족되었다.
$n{\hat {p}}\geq 10$ n $n=400$ = $n=400$ $n=400$ ${\hat {p}}=0.68$ p $n=400$ $n{\hat {p}}\geq 10$ ${\hat {p}}=0.68$ = 0 $68 {\displaystyle {\p$ $p$ $}}}{\$ $displaystyle$ ${p}\geq$ $n(1-{\hat {p}})\geq 10$ $}$ $n(1-{\hat {p}})\geq 10$ n ( $n(1-{\hat {p}})\geq 10$ - p $^){p}\displaystystyn(1-{p}})\geq 10}$

(400)(0.68)\geq 10\Rightarrow 272\geq 10

)

(400)(0.68)\geq 10\Rightarrow 272\geq 10

(

(400)(0.68)\geq 10\Rightarrow 272\geq 10

)

(400)(0.68)\geq 10\Rightarrow 272\geq 10

(400)(0.68)\geq 10\Rightarrow 272\geq 10

(400)(0.68)\geq 10\Rightarrow 272\geq 10

(400)(0.68)\geq 10\Rightarrow 272\geq 10

(400)(0.68)\geq 10\Rightarrow 272\geq 10

(400)(0.68)\geq 10\Rightarrow 272\geq 10

(\displaystyle (400)\geq 10\jeq 10

및 (

(400)(1-0.68)\geq 10\Rightarrow 128\geq 10

)

(400)(1-0.68)\geq 10\Rightarrow 128\geq 10

(400)(1-0.68)\geq 10\Rightarrow 128\geq 10

(400)(1-0.68)\geq 10\Rightarrow 128\geq 10

128

(400)(1-0.68)\geq 10\Rightarrow 128\geq 10

(400)(1-0.68)\geq 10\Rightarrow 128\geq 10

(

1

-

0.

geq 128 ≥

10

(

1-0

.68

)\jeq 128\jeq 10}

정상성의 조건이 충족되었다.

$N$ $N$ 을(를) 이 민주주의의 유권자 인구 크기로 하고 $N$ , $n=400$ = $n=400$ $n=400$ 으로 합시다 $n=400$ $N\geq 10n$ N $N\geq 10n$ $N\geq 10n$ {\ $displaystyle N\geq 10n}$ 이 $N\geq 10n$ 가) 있다면 독립성이 있다.

N\geq 10(400)\오른쪽 화살표 N\geq 4000

이 민주주의 유권자의 인구

N

N

N

은(는) 적어도 4,000명이라고 가정할 수 있다. 따라서 독립의 조건이 충족되었다.

추론 조건이 검증되면 신뢰 구간을 구성할 수 있다.

${\hat {p}}=0.68,n=400,$ ${\hat {p}}=0.68,n=400,$ = ${\hat {p}}=0.68,n=400,$ n ${\hat {p}}=0.68,n=400,$ = ${\hat {p}}=0.68,n=400,$ ${\p}=0.68,n=400,$ 및 $C=0.95$ = $C=0.95$ $C=0.95$

$∗{\$ 에 대해 ${\frac {1-C}{2}}$ 하려면 1 ${\frac {1-C}{2}}$ - ${\frac {1-C}{2}}$ ${\frac {1-C}{2}}$ ${\$ 라는 식을 사용한다 ${\frac {1-C}{2}}$ $z^{*}$

${\frac {1-C}{2}}={\frac {1-0.95}{2}}={\frac {0.05}{2}}=0.0250$

Z\leq z^{*}

꼬리

Z\leq z^{*}

면적이 0.0250이고

Z

에 대한

면적

이 0

.

9750인 z with

z^{*}

z^{*}

을(를) 가진 표준 정규 곡선

Z\leq z^{*}

Z

Z\leq z

Z\leq z

{\displaystyle Z\leq

z

}

에 대한 표준 정규 확률의 표

Z\leq z

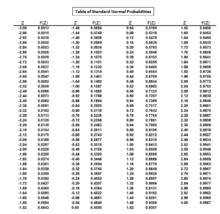
$z^{*}$ 정상 벨 곡선을 조사하여 z $∗{\$ z $^{*}}$ 에 대한 값은 표준 정상 곡선에 0.0250의 위쪽 꼬리 부분 또는 1 - 0.0250 = 0.9750의 면적을 제공하는 표준 점수를 식별하여 결정할 수 있다 $z^{*}$ . $∗{\$ 의 값은 표준 정규 확률 표를 통해서도 확인할 수 있다 $z^{*}$ .

$표준$ 정규 확률 표에서 면적이 $Z$ 0.9750인 Z $Z$ 의 값은 1.96이다. 따라서 $z^{*}$ $∗{\$ z $^{*}}$ 의 값은 1.96이다 $z^{*}$ .

${\hat {p}}=0.68$ = ${\hat {p}}=0.68$ ${\displaystyle$ {\ $p}=0.$ 68 ${\hat {p}}=0.68$ $n=400$ = $n=400$ {\ $displaystyle n=400$ $z^{*}=1.96$ = $z^{*}=1.96$ {\ $displaystyle$ z $^{*}=1.$ 96 $}$ 의 값은 이제 Z 간격에서 1-표본 비율 공식으로 대체할 수 $z^{*}=1.96$ 있다.

${\hat {p}}\pm z^{*}{\sqrt {\frac {{\hat {p}}(1-{\hat {p}})}{n}}}\Rightarrow (0.68)\pm (1.96){\sqrt {\frac {(0.68)(1-0.68)}{(400)}}}\Rightarrow 0.68\pm 1.96{\sqrt {0.000544}}$ $\Rightarrow {\bigl (}0.63429,0.72571{\bigr )}}$

추론 조건과 Z간격의 1표본 비율 공식에 근거해 볼 때 이 민주주의에서 B 후보를 지지하는 유권자의 비율이 63.429%에서 72.571% 사이라는 95% 신뢰수준으로 결론을 내릴 수 있다.

신뢰 구간 범위의 모수 값

추정 통계에서 일반적으로 묻는 질문은 모수가 신뢰 구간 내에 포함되는지 여부다. 이 질문에 대답할 수 있는 유일한 방법은 인구조사를 실시하는 것이다. 위에 제시된 예를 참조하여 모집단 비율이 신뢰 구간의 범위에 있을 확률은 1 또는 0이다. 즉, 매개변수가 구간 범위에 포함되거나 포함되지 않는다. 신뢰 구간의 주요 목적은 모수에 대한 이상적인 값이 될 수 있는 것을 더 잘 보여주는 것이다.

추정에 의한 일반적인 오류 및 잘못된 해석

신뢰구간의 구성에서 발생하는 매우 일반적인 오류는 신뢰수준 $C=95\%$ C = $C=95\%$ % $[\displaystyle$ C $=95\%})$ 이 95% 확률을 의미한다는 믿음이다. 이것은 틀렸다. 자신감의 수준은 확률이 아니라 확실성의 척도에 근거한다. 따라서 $C$ $C$ 의 값은 0과 1 사이에만 $C$ 해당되며, 이 값은 단독으로 적용된다.

순위 집합 표본 추출에 의한 P 추정

P의 더 정확한 추정치는 단순 무작위 표본^[7] 추출 대신 순위 설정 표본 추출 선택으로 얻을 수 있다.

참고^[8] 항목

참조

^ Introduction to Statistical Investigations. Wiley. 18 August 2014. ISBN 978-1-118-95667-0.
^ Ott, R. Lyman (1993). An Introduction to Statistical Methods and Data Analysis. ISBN 0-534-93150-2.
^ ^a ^b ^c Weisstein, Eric W. "Sample Proportion". mathworld.wolfram.com. Retrieved 2020-08-22.
^ "6.3: The Sample Proportion". Statistics LibreTexts. 2014-04-16. Retrieved 2020-08-22.
^ Weisstein, Eric (1998). CRC Concise Encyclopedia of Mathematics. Chapman & Hall/CRC. Bibcode:1998ccem.book.....W.
^ Hinders, Duane (2008). Annotated Teacher's Edition The Practice of Statistics. ISBN 978-0-7167-7703-8.
^ Abbasi, Azhar Mehmood; Yousaf Shad, Muhammad (2021-05-15). "Estimation of population proportion using concomitant based ranked set sampling". Communications in Statistics - Theory and Methods: 1–22. doi:10.1080/03610926.2021.1916529. ISSN 0361-0926. S2CID 236554602.
^ Abbasi, Azhar Mehmood; Shad, Muhammad Yousaf (2021-05-15). "Estimation of population proportion using concomitant based ranked set sampling". Communications in Statistics - Theory and Methods: 1–22. doi:10.1080/03610926.2021.1916529. ISSN 0361-0926. S2CID 236554602.

[1] Introduction to Statistical Investigations. Wiley. 18 August 2014. ISBN 978-1-118-95667-0.

[2] Ott, R. Lyman (1993). An Introduction to Statistical Methods and Data Analysis. ISBN 0-534-93150-2.

[:0-3] Weisstein, Eric W. "Sample Proportion". mathworld.wolfram.com. Retrieved 2020-08-22.

[4] "6.3: The Sample Proportion". Statistics LibreTexts. 2014-04-16. Retrieved 2020-08-22.

[5] Weisstein, Eric (1998). CRC Concise Encyclopedia of Mathematics. Chapman & Hall/CRC. Bibcode:1998ccem.book.....W.

[6] Hinders, Duane (2008). Annotated Teacher's Edition The Practice of Statistics. ISBN 978-0-7167-7703-8.

[7] Abbasi, Azhar Mehmood; Yousaf Shad, Muhammad (2021-05-15). "Estimation of population proportion using concomitant based ranked set sampling". Communications in Statistics - Theory and Methods: 1–22. doi:10.1080/03610926.2021.1916529. ISSN 0361-0926. S2CID 236554602.

[8] Abbasi, Azhar Mehmood; Shad, Muhammad Yousaf (2021-05-15). "Estimation of population proportion using concomitant based ranked set sampling". Communications in Statistics - Theory and Methods: 1–22. doi:10.1080/03610926.2021.1916529. ISSN 0361-0926. S2CID 236554602.

[1]

[2]

[3]

[4]

[5]

[7]

[8]

Search