이동형 세포자동화

이 글에는 참고문헌, 관련 독서 또는 외부 링크 목록이 수록되어 있으나 인라인 인용구가 부족하여 출처가 불분명하다. 좀 더 정밀한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오. (2014년 5월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

이동성 세포자동화법

두 표면 사이의 인터페이스에서 마찰을 시뮬레이션하는 데 사용되는 이동식 셀룰러 자동화의 애니메이션
방법 유형
연속/분리	이산형
분석/컴퓨팅	연산
특성.
영향을 받은	세포 자동자, 이산 요소
메서드 인	계산 고형 역학

이동식 셀룰러 오토매틱(MCA) 방법은 이산 개념에 기초한 고체 역학을 계산하는 방법이다. 그것은 고전적인 세포 자동화와 이산 요소 방법의 장점을 모두 제공한다. MCA 방법의 한 가지 중요한 장점은^[1] 손상 발생, 균열 전파, 단편화, 질량 혼합을 포함한 재료 파괴의 직접적인 시뮬레이션을 허용한다는 것이다. 연속역학 방법(예: 유한요소법, 유한차량법 등)에 의해 이러한 과정을 시뮬레이션하는 것은 어렵기 때문에 근역학과 같은 새로운 개념이 필요하다. 이산 원소법은 미세한 물질을 시뮬레이션하는 데 매우 효과적이지만 이동 가능한 셀룰러 오토마타 사이의 상호 힘은 고형분 행동을 시뮬레이션한다. 자동자의 세포 크기가 0에 가까워짐에 따라 MCA 동작은 고전적인 연속체 역학 방법에 접근한다.^[2] MCA 방법은 S.G. Psakie의 그룹에서 개발되었다.

이동형 셀룰러 자동기법의 키스톤

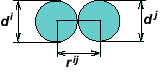
MCA 접근방식의 프레임워크에서 모델링 대상 물체는 상호 작용하는 요소/오토마타의 집합으로 간주된다. 오토마타 세트의 역학은 그들의 관계에 대한 상호 힘과 규칙에 의해 정의된다. 이 시스템은 시공간에서 존재하며 작동한다. 시공간에서의 그것의 진화는 움직임의 방정식에 의해 지배된다. 요소 간 관계에 대한 상호 힘과 규칙은 자동 응답 기능에 의해 정의된다. 이 기능은 각 자동화에 대해 지정되어야 한다. 오토마타의 이동성 때문에 다음과 같은 셀룰러 오토마타의 새로운 매개변수를 고려해야 한다: R – 자동화의ⁱ 반지름 벡터, Vⁱ – 자동화의 속도, Ωⁱ – 자동화의 회전 속도, velocity – 자동화의ⁱⁱ 회전 벡터, m – 자동화의 질량, Jⁱ – 자동화의 관성 모멘트.

새로운 개념: 이웃

MCA 방법의 새로운 개념은 종래의 것 외에 오토마타 쌍의 상태(오토마타 쌍의 상호 작용의 관계)의 도입, 즉 별도의 오토마톤의 상태에 근거한다. 이 정의의 도입은 정적 네트 개념에서 인접 개념으로 가는 것을 허용한다는 점에 유의한다. 그 결과 오토마타는 쌍의 상태(관계)를 바꾸어 이웃을 변화시킬 수 있는 능력을 갖게 된다.

페어 상태 매개변수 정의

새로운 유형의 상태가 도입되면 관계를 전환하기 위한 기준으로 사용하기 위한 새로운 매개변수로 이어진다. 그것은 자동 중복 매개변수^ij h로 정의된다. 따라서 세포 자동자극의 관계는 겹치는 값에 의해 특징지어진다.

초기 구조는 각각의 이웃 요소 쌍들 사이에 일정한 관계를 설정함으로써 형성된다.

페어 관계 상태 전환 기준

MCA 방법의 고전적인 세포 자동 방식과 대조적으로, 단일 자동화는 물론 쌍의 오토마타 관계도 전환할 수 있다. 바이스트 가능 자동타 개념에 따라 두 가지 유형의 쌍 상태(관계)가 있다.

연계된	– 두 오토마타는 모두 고체에 속한다.
연계가 없는	– 쌍의 각 자동화는 서로 다른 신체 또는 손상된 신체의 일부에 속한다.

그래서 쌍 관계 상태의 변화는 오토마타의 상대적인 움직임에 의해 제어되며, 그러한 쌍들에 의해 형성된 매체는 바이스트 가능한 매체로 간주될 수 있다.

MCA 운동 방정식

MCA 미디어의 진화는 다음과 같은 번역 동작 방정식으로 설명된다.

${\displaystyle {d^{2}h^{ij} \over dt^{2}}=\left({1 \over m^{i}}+{1 \over m^{j}}\right)p^{ij}+\sum _{k\neq j}C(ij,ik)\psi (\alpha _{ij,ik}){1 \over m^{i}}p^{ik}+\sum _{l\neq i}C(ij,jl)\psi (\alpha _{ij,jl}){1 \over m^{j}}p^{jl}}$

여기서 $m{\displaystyle {}^{}}$ ${\displaystyle i^{}}$ ${\$ m$^{i}$는 $오토마톤{\displaystyle }$ i ${\displaystyle$ $i},$ $p$ ${\displaystyle i^{}}$ ${\displaystyle j^{}}$ ${\$$displaystyle p^{ij}}$는 $automata{\displaystyle }$ i ${\$$displaysty$ $j$ $(ij,ik)$ 사이에서 작용하는 중심력으로서$$ hpar 전송과 관련된 확실한 계수다$$.j (${\displaystyle {}_{}}$ ${\displaystyle {\mathrm{ij}}_{}}$, i $){\displaystyle \psi (\alpha _{ij,ik}})$는 ij와 ik의 방향 사이의 각도다$$.

이동 가능한 자동자의 크기가 한정되어 있기 때문에 회전 효과를 고려해야 한다. 회전 운동 방정식은 다음과 같이 쓸 수 있다.

${\displaystyle {d^{2}\theta ^{ij} \over dt^{2}}=\left({q^{ij} \over J^{i}}+{q^{ji} \over J^{j}}\right)\tau ^{ij}+\sum _{k\neq j}S(ij,ik){q^{ik} \over J^{i}}\tau ^{ik}+\sum _{l\neq j}S(ij,jl){q^{jl} \over J^{j}}\tau ^{jl}}$

automaton 나는 순서 행동 j(모멘트 팔)의 관점 있는 연락처 중심에서 상대적인 회전(hij처럼 번역을 위해 교환 매개 변수)여기 Θij는 각도, qij하는 거리, τij은 쌍 접선 상호 작용, S){S(ij,ik)\displaystyle}은 특정한 계수는Θ 매개 변수 전달과 관련된입니다. 하나에서 다른 것과 짝을 이루다(번역을 위한 방정식의$$ $){\displaystyle C(ij,ik)}$와 유사하다.

이 방정식은 다-입자 접근방식의 운동 방정식과 완전히 유사하다.

오토마타 쌍의 변형 정의

쌍 automata 변환 i j automata 쌍의 변환을 위한 치수 없는 변형 매개변수는 다음과 같이 나타낼 수 있다.

${\displaystyle \varepsilon ^{ij}={h^{ij} \over r_{0}^{ij}}={\left(q^{ij}+q^{ji}\right)-\left(d^{i}+d^{j}\right){\big /}2 \over \left(d^{i}+d^{j}\right){\big /}2}}$

이 경우:

${\displaystyle \left(\Delta {\varepsilon ^{i(j)}}+d^{j}\right){{{n}^{n}}}\delta {t}}이상 \}$

여기서 Δt 시간 단계, V_n^ij – 상대 속도.

쌍 오토마타의 회전은 마지막 번역 관계와 유추하여 계산할 수 있다.

MCA 방식에서의 되돌릴 수 없는 변형 모델링

ε^ij 매개변수는 automaton j와 상호작용하는 automaton i의 변형 척도로 사용된다. 여기서 q^ij – 는 automaton i의 중심에서 automaton j와의 접촉 지점까지의 거리; Rⁱ = dⁱ/2 (dⁱ –는 automaton i의 크기이다.

예를 들어, 반복하중을 받는 티타늄 시료(긴장 – 압축)가 고려된다. 적재 다이어그램은 다음 그림에 표시된다.

적재 방식	로딩 다이어그램
	(빨간색 표시는 실험 데이터)

MCA 방식의 장점

각 자동화의 이동성 때문에 MCA 방법은 다음과 같은 조치를 직접 고려할 수 있다.

• 매스 믹싱
• 침투 효과
• 화학 반응
• 집약 변형
• 위상 변환
• 손해의 누적
• 분열과 골절
• 균열 발생과 발전

다른 유형의 경계 조건(고정, 탄성, 점성 탄성 등)을 사용하면 시뮬레이션 시스템을 포함하는 주변 매체의 다른 특성을 모방할 수 있다. 경계에 추가 조건을 설정함으로써 다양한 기계적 하중 모드(긴장, 압축, 전단 변형 등)를 모델링할 수 있다.

참고 항목

• 연속체 역학 – 연속체 질량으로 모델링된 물질의 거동을 연구하는 물리학과
• 고체 역학 – 고체 물질과 그 거동에 관련된 역학의 분과
• 파단 역학 – 재료의 균열 확산에 관한 연구와 관련된 역학
• 페리디나믹스
• 컴퓨터 시뮬레이션 – 컴퓨터에서 수행되는 수학적 모델링 프로세스
• 이산 원소법 – 다수의 소립자의 움직임과 효과를 계산하는 수치적 방법
• 셀룰러 오토매틱 – 컴퓨터 과학 분야에서 연구된 이산 모델
• 유한요소법 – 물리 또는 공학적 문제 해결을 위한 수치적 방법
• 유한차법

참조

• Psakhie, S.G.; Horie, Y.; Korostelev, S.Yu.; Smolin, A.Yu.; Dmitriev, A.I.; Shilko, E.V.; Alekseev, S.V. (November 1995). "Method of movable cellular automata as a tool for simulation within the framework of mesomechanics". Russian Physics Journal. 38 (11): 1157–1168. doi:10.1007/BF00559396. S2CID 120300401.
• Psakhie, SG보험 증권.;Korostelev, S.Y.;Smolin, A.Y.;Dmitriev, A.나;Shilko, 집 수리, Moiseenko 감별 진단.;Tatarincev E.M.;알렉세예프, S.V.(1998년)."재료의 물리적 mesomechanics 위한 도구로 이동할 수 있는 세포 메서드".물리적 Mesomechanics.1(1):95–108.(Псахье, С.Г.;Коростелев, С.Ю.;Смолин, А.Ю.;Дмитриев, А.И.;Шилько, Е.В.;Моисеенко, Д.Д.;Татаринцев, Е.М.;Алексеев, С.В.(1998년)."Метод подвижных клеточных автоматов как инструмент физической мезомеханики материалов".Физическая мезомеханика. 1(1):95–108.. 2010-03-03 Retrieved)
• Psakhie, SG보험 증권.;Ostermeyer, GloriaPatri어.;Dmitriev, A.나;Shilko, 집 수리, Smolin, A.Y, Korostelev, S.Y.(2000년).수치 개별 역학에 새로운 방향으로 "이동할 수 있는 세포 방법이다.대한 description".물리적 Mesomechanics.3(2):5–13.(Псахье, С.Г.;Остермайер, Г.П.;Дмитриев, А.И.;Шилько, Е.В.;Смолин, А.Ю.;Коростелев, С.Ю.(2000년)."Метод подвижных клеточных автоматов как новое направление дискретной вычислительной механики.나 Теоретическое описание".Физическая мезомеханика. 3(2):5–13.. 2010-03-03 Retrieved)
• Psakhie, S.G.; Horie, Y.; Ostermeyer, G.P.; Korostelev, S.Yu.; Smolin, A.Yu.; Shilko, E.V.; Dmitriev, A.I.; Blatnik, S.; Spegel, M.; Zavsek, S. (December 2001). "Movable cellular automata method for simulating materials with mesostructure" (PDF). Theoretical and Applied Fracture Mechanics. 37 (1–3): 311–334. doi:10.1016/S0167-8442(01)00079-9. Archived from the original (PDF) on 2011-07-19.
• Psakhie, S.G.; Smolin, A.Y.; Stefanov, Y.P.; Makarov, P.V.; Chertov, M.A. (2004). "Modeling the behavior of complex media by jointly using discrete and continuum approaches". Technical Physics Letters. 30 (9): 712–714. doi:10.1134/1.1804572. S2CID 120067680.
• Shimizu, Y.; Hart, R.; Cundall, P. (2004). Numerical modeling in Micromechanics via Particle Methods. ISBN 978-90-5809-679-1. Retrieved 2010-03-03.
• Gnecco, E.; Meyer E., eds. (2007). Fundamentals of friction and wear on the Nanoscale. ISBN 978-3-540-36806-9. Retrieved 2010-03-03.
• Yunliang, Tan; Guirong, Teng; Haitao, Li (2008). "MCA Model for Simulating the Failure of Microinhomogeneous Materials". Journal of Nanomaterials. 2008: 1–7. doi:10.1155/2008/946038. 946038.
• Fomin, V.M.;안드레 예프, A.N.;et 알.(2008년).이산 연속까지 Mechanics-.과학의 적용되었고 이론적 역학의 러시아 학원, 시베리아 지부 연구소(SA의 이름Khristianovich cm이다.우편 344.아이 에스비엔 978-5-7692-0974-1.(Фомин, В.М.;Андреев А.Н. и др.(2008년).Механика-отсплошному(러시아어로)к дискретного.Рос. акад наук, Сиб. отд-ние, Ин-т теоретической и прикладной механики им. С.А. Христиановича. 우편 344.아이 에스비엔 978-5-7692-0974-1.62011년 10월에 원래에서 Archived.3월 3일 2010년 Retrieved)
• Smolin, A.Y.; Roman, N.V.; Dobrynin, S.A.; Psakhie, S.G. (May–August 2009). "On rotation in the movable cellular automaton method". Physical Mesomechanics. 12 (3–4): 124–129. doi:10.1016/j.physme.2009.07.004.
• Popov, Valentin L. (2009). Kontaktmechanik und Reibung (Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation). Springer Berlin Heidelberg. doi:10.1007/978-3-540-88837-6. ISBN 978-3-540-88836-9.
• 도브리닌, SA(2010년).고체의 접촉 상호 작용 아래 탄성 파도의 생성 및 전파 모델 일을 가동 세포 atomaton 법의 개발.톰스크:물리학과 수학의 PhD 논문. 우편 130.(Добрынин, С.А.(2010년).Развитие метода подвижных клеточных автоматов для моделирования генерации и распространения упругих волн при контактном взаимодействии твердых тел(러시아어로).Томск:Диссертация지만кандидата физико-математических наук. 우편 130.3월 3일 2010년.)Retrieved.
• 도브리닌, 세르게이(2011년).가동 세포 automaton 법에 의한 컴퓨터 시뮬레이션.자르브뤼켄. 독일:LAPLAMBERT 학술 출판사예요. 우편 132.아이 에스비엔 978-3-8443-5954-1.(Добрынин, Сергей(2011년).Компьютерное моделирование методом подвижных клеточных автоматов(러시아어로).자르브뤼켄. 독일:LAPLAMBERT 학술 출판사예요. 우편 132.아이 에스비엔 978-3-8443-5954-1.. 2011-11-19 Retrieved)

소프트웨어

• MCA 소프트웨어 패키지
• 이산 연속 접근 방식의 재료 시뮬레이션 소프트웨어 softwareFEM+MCA »: AFAS(Application Research Foundation of Algorithm and Software)의 국가 등록 수: 50208802297 / Smolin A.Y, Zelepugin S.A, Dobryin S.A.A.; 신청자 및 개발 센터는 톰스크 주립대학이다. – 등록 날짜 28.11.18; 인증서 AFAS N 11826 날짜 01.12.18.