모듈로 연산

연산에서 모듈로 연산은 한 숫자를 다른 숫자로 나눈 후(연산의 계수라고 함) 나눗셈의 나머지 또는 부호 있는 나머지를 반환합니다.

두 개의 $양수$ $a$ 와 n이 주어졌을 때, 모듈로 $n$ (종종 $mod$ n $또는$ % $n$ 으로 줄임)은 유클리드 나눗셈의 $나머지$ 이다. 여기서 $a$ 는 $배당$ 이고 n은 제수이다.모듈로 연산은 동작하고 있는 모듈러스^[1](또는 제수)를 나타내는 $기호모드$ 와 구별해야 합니다.

예를 들어, "5 mod 2"는 5를 2로 나누면 2의 몫이 되고 나머지 1이 되기 때문에 "5 mod 2"는 1로 평가되며, "9 mod 3"은 0으로 평가됩니다. 9를 3으로 나누면 3의 몫이 되고 나머지 0이 되기 때문에 3을 곱한 후에는 9에서 빼는 것이 없습니다.

일반적으로 $a$ 와 n이 모두 정수인 상태에서 수행되지만, 많은 컴퓨팅 시스템에서는 다른 유형의 숫자 오퍼랜드가 허용됩니다. $n$ 의 정수 모듈로 연산의 값의 범위는 0 ~ $n$ - $1$ 입니다( $mod$ 1은 항상 0이고 $mod$ 0은 정의되어 있지 않기 때문에 일부 프로그래밍 언어에서는 0으로 나눗셈 오류가 발생할 수 있습니다).숫자 이론에서 적용되는 오래된 관련 규칙에 대해서는 모듈식 산술을 참조하십시오.

a $또는$ n 중 $하나$ 가 음수일 경우 순진한 정의는 분해되며 프로그래밍 언어에 따라 이들 값의 정의 방법이 달라집니다.

정의의 변형

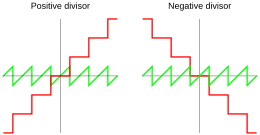
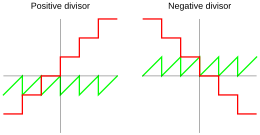
수학에서, 모듈로 연산의 결과는 동등성 클래스이며, 클래스의 어떤 구성원도 대표적으로 선택될 수 있다. 그러나, 통상적인 대표자는 그 클래스에 속하는 최소 양의 잔차, 가장 작은 음의 정수이다(즉, 유클리드 ^[2]나눗셈의 나머지).그러나 다른 표기법도 가능합니다.컴퓨터와 계산기에는 숫자를 저장하고 표현하는 다양한 방법이 있습니다. 따라서 모듈로 연산의 정의는 프로그래밍 언어 또는 기본 하드웨어에 따라 달라집니다.

거의 모든 컴퓨팅 시스템에서 $몫$ q와 a를 n으로 $나눈$ $나머지$ r은 다음 조건을 충족합니다.

(\displaystyle\displaystyle{aligned}q,\in\mathbb {Z} \a,=nq+r\r\r &< n \end{aligned})

(1)

그러나, 나머지가 0이 아닌 경우, 이것은 여전히 부호 모호성을 남깁니다: 나머지에 대한 두 가지 가능한 선택, 하나는 음수이고 다른 하나는 양수이고, 그리고 두 가지 가능한 선택들이 지수에 대해 발생합니다.숫자 이론에서는 항상 양의 나머지가 선택되지만, 컴퓨팅에서는 프로그래밍 언어는 언어와 a $또는$ ^[a] $n$ 의 부호에 따라 선택됩니다.예를 들어 표준 Pascal 및 ALGOL 68은 음의 제수에 대해서도 양의 나머지(또는 0)를 부여하며, C90과 같은 일부 프로그래밍 언어는 n $또는$ a $중$ 하나가 음의 경우 구현에 맡깁니다(자세한 내용은 §의 표 참조).modulo 0은 대부분의 시스템에서 정의되어 있지 않지만 일부에서는 $a$ 로 정의되어 $있습니다$ .

잘린 나눗셈을 사용하여 배당( $a$ )의 함수로서의 몫( $q$ )과 나머지( $r$ )
많은 구현에서는 잘린 나눗셈을 사용합니다.여기서 몫은 잘라내기( ${\textstyle q=\operatorname {trunc} \left({\frac {a}{n}}\right)}$ 부분) q ${\textstyle q=\operatorname {trunc} \left({\frac {a}{n}}\right)}$ ${\textstyle q=\operatorname {trunc} \left({\frac {a}{n}}\right)}$ ( ${\textstyle q=\operatorname {trunc} \left({\frac {a}{n}}\right)}$ ) { $textstyle$ q = \ $operatorname {snc$ } \ $lefts\frac$ { $a}{n}}}}}$ }로 정의되며 ${\textstyle q=\operatorname {trunc} \left({\frac {a}{n}}\right)}$ , 따라서 등식 (1)에 따라 나머지는 배당과 같은 부호를 가집니다.이 몫은 0을 향해 반올림됩니다: 정확한 유리 몫에서 0 방향의 첫 번째 정수와 같습니다.
$({displaystyle r=a-n\operatorname {c}\leftfrac {a}{n}}\right)$
플로어 나눗셈을 사용한 몫과 나머지
Donald^[3] Knuth는 바닥 ${\textstyle q=\left\lfloor {\frac {a}{n}}\right\rfloor }$ q ${\textstyle q=\left\lfloor {\frac {a}{n}}\right\rfloor }$ ${\textstyle q=\left\lfloor {\frac {a}{n}}\right\rfloor }$ a ${\textstyle q=\left\lfloor {\frac {a}{n}}\right\rfloor }$ { $textstyle$ q ${\textstyle q=\left\lfloor {\frac {a}{n}}\right\rfloor }$ = \ left \ $lfloor }$ { frac { a $}$ \ right \ $loor$ }에 ${\textstyle q=\left\lfloor {\frac {a}{n}}\right\rfloor }$ 의해 정의되는 바닥 나눗셈을 설명했다. 따라서 방정식 (1)에 따르면 나머지는 제수와 같은 부호를 가질 것이다.바닥 함수로 인해 이미 음수인 경우에도 항상 아래쪽으로 반올림됩니다.
$(\displaystyle r=a-n\left\lfloor\frac {a}{n}\right\loor})$
유클리드 나눗셈을 사용한 몫과 나머지
레이먼드 T.부테는^[4] 나머지가 항상 음이 아닌 0 $µ r$ 인 유클리드 정의를 기술하고, 따라서 유클리드 나눗셈 알고리즘과 일치한다.이 경우,
$\displaystyle n > 0 \ time q = \ lfloor \ frac { a } { n } \ right \ sloor }$

$n<0\lceil q=\left\lceil {frac {a}{n}}\rceil$

또는 동등하게

$q=\operatorname {sgn}(n)\left\lfloor {a}{\left n\right }\right\loor$

$여기$ 서 sgn은 기호 함수이므로

$r=a-n \left\lfloor {\frac {a}{\left n\right }}\right\loor$
반올림 나눗셈을 사용하여 몫과 나머지를 구함
반올림 나눗셈은 ${\textstyle q=\operatorname {round} \left({\frac {a}{n}}\right)}$ $=$ 반올림 ${\textstyle q=\operatorname {round} \left({\frac {a}{n}}\right)}$ θ( $)$ { $textstyle$ q=\ $operatorname {round}$ \ $leftfrac {a}{n}}\right}$ 인 경우 ${\textstyle q=\operatorname {round} \left({\frac {a}{n}}\right)}$ 즉 가장 가까운 정수로 반올림합니다.이것은 Common Lisp 및 IEEE 754에 기재되어 있습니다(IEE-754의 가장 가까운 표기법 참조).따라서 나머지 부호는 0에 가장 가까운 부호로 선택됩니다.
천장 분할을 사용한 몫 및 나머지
공통 리스프는 또한 q ${\textstyle q=\left\lceil {\frac {a}{n}}\right\rceil }$ ${\textstyle q=\left\lceil {\frac {a}{n}}\right\rceil }$ ${\textstyle q=\left\lceil {\frac {a}{n}}\right\rceil }$ ${\textstyle q=\left\lceil {\frac {a}{n}}\right\rceil }$ ${\$ { $textstyle$ q = \ $left$ \ $lceil$ { $frac$ { $a }$ $}$ \ $right$ \ rceil ${\textstyle q=\left\lceil {\frac {a}{n}}\right\rceil }$ 로 주어진 천장 분할(제수와 다른 기호)을 정의합니다.따라서 나머지 부호는 제수와 다르게 선택됩니다.

레이젠이 설명한 바와 같이

부테는 유클리드 나눗셈이 규칙성과 유용한 수학적 특성 면에서 다른 나눗셈보다 우수하다고 주장하지만, 크누스에 의해 추진된 플로어 나눗셈 역시 좋은 정의이다.널리 사용됨에도 불구하고, 잘린 나눗셈은 다른 정의보다 열등한 것으로 나타난다.
--

단, 잘린 나눗셈은 동일성 $({-a})/b={-(a/b)}=a/({-b})$ - $({-a})/b={-(a/b)}=a/({-b})$ ) / $({-a})/b={-(a/b)}=a/({-b})$ $({-a})/b={-(a/b)}=a/({-b})$ - ( $({-a})/b={-(a/b)}=a/({-b})$ / $({-a})/b={-(a/b)}=a/({-b})$ ) $({-a})/b={-(a/b)}=a/({-b})$ / $({-a})/b={-(a/b)}=a/({-b})$ ( - $({-a})/b={-(a/b)}=a/({-b})$ ) { $displaystyle$ ( ( - $a$ / b ) / b $({-a})/b={-(a/b)}=a/({-b})$ = { - ( a / b ) } = $({-a})/b={-(a/b)}=a/({-b})$ a / ( { - $b$ ) $({-a})/b={-(a/b)}=a/({-b})$ ^[6]} 를 만족합니다.

표기법

일부 계산기에는 mod $() 함수$ 버튼이 있고 많은 프로그래밍 언어에는 mod $(a,$ $n)$ 로 표현되는 유사한 함수가 있습니다.일부에서는 "%", "mod" 또는 "Mod"를 모듈로 또는 나머지 연산자로 사용하는 식도 지원합니다.a % n또는a mod n.

유사한 기능이 없는 환경에서는 위의 세 가지 정의 중 하나를 사용할 수 있습니다.

일반적인 함정

모듈로 연산 결과에 배당(정렬 정의)의 부호가 있을 경우, 예기치 않은 실수가 발생할 수 있습니다.

예를 들어, 정수가 홀수인지 여부를 검정하기 위해 2의 나머지가 1인지 검정할 수 있습니다.

부울 홀수(인트 n) {     돌아가다 n % 2 == 1; }

그러나 modulo에 배당 부호가 있는 언어에서는 잘못된 것입니다.n(배당)이 음수이고 홀수일 $경우$ n mod 2는 -1을 반환하고 함수는 false를 반환하기 때문입니다.

한 가지 올바른 대안은 나머지가 0이 아님을 검정하는 것입니다(나머지 0은 부호에 관계없이 동일하기 때문입니다).

부울 홀수(인트 n) {     돌아가다 n % 2 != 0; }

또 다른 대안은 홀수에 대해 나머지가 1 또는 -1이 될 수 있다는 사실을 이용하는 것입니다.

부울 홀수(인트 n) {     돌아가다 n % 2 == 1    n % 2 == -1; }

보다 간단한 대안은 n % 2의 결과를 부울값으로 취급하는 것입니다.여기서 0이 아닌 값은 모두 참입니다.

부울 홀수(인트 n) {     돌아가다 n % 2; }

퍼포먼스 문제

모듈로 연산은 나머지가 있는 나눗셈이 매번 계산되도록 구현될 수 있습니다.특수한 경우 하드웨어에 따라서는 보다 빠른 대체 수단이 존재합니다.예를 들어, 2의 거듭제곱의 모듈로는 비트 단위의 AND 연산(x가 $양$ 의 정수라고 가정하거나 비트렁킹 정의를 사용)으로 표현할 수 있습니다.

x % 2ⁿ == x & (2ⁿ - 1)

예:

x % 2 == x & 1

x % 4 == x & 3

x % 8 == x & 7

모듈로보다 비트 단위 연산을 효율적으로 구현하는 디바이스 및 소프트웨어에서는 이러한 대체 형식을 사용하면 계산이 ^[7]더 빨라질 수 있습니다.

컴파일러 최적화는 폼의 식을 인식할 수 있습니다.expression % constant어디에constant2의 거듭제곱으로 자동으로 구현됩니다.expression & (constant-1)이를 통해 프로그래머는 성능을 저하시키지 않고 더 선명한 코드를 작성할 수 있습니다.이 간단한 최적화는 부호 없는 정수형이 아닌 한 모듈로 연산 결과에서 배당의 부호(C 포함)가 있는 언어에서는 불가능합니다.왜냐하면, 만약 배당이 음수라면, 모듈로는 음수가 될 것이고, 반면,expression & (constant-1)항상 긍정적일 것이다.이 언어들의 경우, 동등성은x % 2ⁿ == x < 0 ? x ~(2ⁿ - 1) : x & (2ⁿ - 1)대신 비트 OR, NOT 및 AND 연산을 사용하여 표현해야 합니다.

일반 상수-계수 연산을 위한 최적화도 상수-divisor 최적화를 사용하여 먼저 나눗셈을 계산함으로써 존재합니다.

속성(아이덴티티)

일부 모듈로 연산은 다른 수학적 연산과 유사하게 인수분해되거나 확장될 수 있습니다.이것은 Diffie와 같은 암호 증명에 도움이 될 수 있습니다.Hellman 키 교환.이러한 속성 중 일부는 $a$ 와 n을 $정수$ 여야 합니다.

아이덴티티:
- ( $a$ $mod$ n) $mod$ n = $a$ $mod$ n $.$
- $x$ 의^x 모든 양의 정수 $값$ 에 대해 n $mod$ n = 0입니다.
- $만약$ p가 $b$ 의 제수가 아닌 소수라면, 페르마의 작은 정리 때문에 $ab$ mod $p$ =a $mod$ $p$ 이다^p−1.
역:
- $[(-a$ $mod$ n $)$ + ( $a$ $mod$ n $)]$ $mod$ n = $0$ .
- $b -1$ $mod$ n은 모듈식 곱셈 역수를 나타내며, $b$ 와 n이 상대적으로 소수인 $경우$ 에만 정의된다. 이것은 왼쪽 변이 정의되는 경우이다: $[(b -1$ $mod$ n $)(b$ $mod$ n $)]$ $mod$ n = $1$ .
배포:
- $(a$ + $b)$ $mod$ n = $[(a$ $mod$ n $)$ + ( $b$ $mod$ n $)] mod$ n.
- $ab$ $mod$ n = [( $a$ $mod$ n $)(b$ $mod$ n $)] mod$ n.
사단(정의):.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{.Border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}a/b 모드 nx[(모드 족인지 조차 nx(b−1 모드 nx]mod, 오른쪽 손 쪽, 그렇지 않으면 한정되지 않은( 때 b와 엔coprime다)정의된다.
역 곱셈: $[(ab$ $mod$ n $)(b -1$ $mod$ n $)]$ $mod$ n = $a$ $mod$ n.

프로그래밍 언어

다양한 프로그래밍 언어의 모듈로 연산자
언어	교환입니다.	정수	부동 소수점	정의.
ABAP	`MOD`	네.	네.	유클리드
액션 스크립트	`%`	네.	아니요.	잘렸다
아다	`mod`	네.	아니요.	플로어^[8]
아다	`rem`	네.	아니요.	잘렸다^[8]
알골 68	`÷×`,`mod`	네.	아니요.	유클리드
앰프	`mod`	네.	아니요.	잘렸다
APL	^[b]	네.	아니요.	플로어
애플 스크립트	`mod`	네.	아니요.	잘렸다
자동 LISP	`(rem d n)`	네.	아니요.	잘렸다
AWK	`%`	네.	아니요.	잘렸다
기본의	`Mod`	네.	아니요.	정의되어 있지 않다
bc	`%`	네.	아니요.	잘렸다
C C++	`%`,`div`	네.	아니요.	잘렸다^[c]
	`fmod`(C) `std::fmod`(C++)	아니요.	네.	잘렸다^[11]
	`remainder`(C) `std::remainder`(C++)	아니요.	네.	반올림
C#	`%`	네.	네.	잘렸다
클라리온	`%`	네.	아니요.	잘렸다
깨끗한	`rem`	네.	아니요.	잘렸다
클로쥬르	`mod`	네.	아니요.	플로어^[12]
클로쥬르	`rem`	네.	아니요.	잘렸다^[13]
코볼	`FUNCTION MOD`	네.	아니요.	플로어^[d]
커피 스크립트	`%`	네.	아니요.	잘렸다
커피 스크립트	`%%`	네.	아니요.	플로어^[14]
콜드퓨전	`%`,`MOD`	네.	아니요.	잘렸다
일반적인 리스프	`mod`	네.	네.	플로어
일반적인 리스프	`rem`	네.	네.	잘렸다
크리스탈	`%`,`modulo`	네.	네.	플로어
크리스탈	`remainder`	네.	네.	잘렸다
D	`%`	네.	네.	잘렸다^[15]
다트	`%`	네.	네.	유클리드^[16]
다트	`remainder()`	네.	네.	잘렸다^[17]
에펠	`\\`	네.	아니요.	잘렸다
엘릭시르	`rem/2`	네.	아니요.	잘렸다^[18]
엘릭시르	`Integer.mod/2`	네.	아니요.	플로어^[19]
느릅나무	`modBy`	네.	아니요.	플로어^[20]
느릅나무	`remainderBy`	네.	아니요.	잘렸다^[21]
얼랑	`rem`	네.	아니요.	잘렸다
얼랑	`math:fmod/2`	아니요.	네.	잘림(^[22]C와 동일)
행복감	`mod`	네.	아니요.	플로어
행복감	`remainder`	네.	아니요.	잘렸다
F#	`%`	네.	네.	잘렸다
요인	`mod`	네.	아니요.	잘렸다
파일 메이커	`Mod`	네.	아니요.	플로어
넷째	`mod`	네.	아니요.	구현 정의
	`fm/mod`	네.	아니요.	플로어
	`sm/rem`	네.	아니요.	잘렸다
포트란	`mod`	네.	네.	잘렸다
포트란	`modulo`	네.	네.	플로어
프링크	`mod`	네.	아니요.	플로어
GLSL	`%`	네.	아니요.	정의되어 있지^[23] 않다
GLSL	`mod`	아니요.	네.	플로어^[24]
GameMaker Studio (GML)	`mod`,`%`	네.	아니요.	잘렸다
GDScript(Godot)	`%`	네.	아니요.	잘렸다
	`fmod`	아니요.	네.	잘렸다
	`posmod`	네.	아니요.	플로어
	`fposmod`	아니요.	네.	플로어
가세요	`%`	네.	아니요.	잘렸다^[25]
	`math.Mod`	아니요.	네.	잘렸다^[26]
	`big.Int.Mod`	네.	아니요.	유클리드^[27]
그루비	`%`	네.	아니요.	잘렸다
하스켈	`mod`	네.	아니요.	플로어^[28]
	`rem`	네.	아니요.	잘렸다^[28]
	`Data.Fixed.mod'`(GHC)	아니요.	네.	플로어
Haxe	`%`	네.	아니요.	잘렸다
HLSL	`%`	네.	네.	정의되어 있지^[29] 않다
J	^[b]	네.	아니요.	플로어
자바	`%`	네.	네.	잘렸다
자바	`Math.floorMod`	네.	아니요.	플로어
자바스크립트 타입 스크립트	`%`	네.	네.	잘렸다
줄리아.	`mod`	네.	네.	플로어^[30]
줄리아.	`%`,`rem`	네.	네.	잘렸다^[31]
코틀린	`%`,`rem`	네.	네.	잘렸다^[32]
코틀린	`mod`	네.	네.	플로어^[33]
ksh	`%`	네.	아니요.	잘림(POSIX sh와 동일)
ksh	`fmod`	아니요.	네.	잘렸다
랩뷰	`mod`	네.	네.	잘렸다
Libre Office	`=MOD()`	네.	아니요.	플로어
로고	`MODULO`	네.	아니요.	플로어
로고	`REMAINDER`	네.	아니요.	잘렸다
루아 5	`%`	네.	네.	플로어
루아 4	`mod(x,y)`	네.	네.	잘렸다
리버티 바스IC	`MOD`	네.	아니요.	잘렸다
매스캐드	`mod(x,y)`	네.	아니요.	플로어
메이플	`e mod m`(디폴트),`modp(e, m)`	네.	아니요.	유클리드
	`mods(e, m)`	네.	아니요.	반올림
	`frem(e, m)`	네.	네.	반올림
매스매티카	`Mod[a, b]`	네.	아니요.	플로어
매트랩	`mod`	네.	아니요.	플로어
매트랩	`rem`	네.	아니요.	잘렸다
막시마	`mod`	네.	아니요.	플로어
막시마	`remainder`	네.	아니요.	잘렸다
Maya 임베디드 언어	`%`	네.	아니요.	잘렸다
Microsoft Excel	`=MOD()`	네.	네.	플로어
Minitab	`MOD`	네.	아니요.	플로어
모듈라-2	`MOD`	네.	아니요.	플로어
모듈라-2	`REM`	네.	아니요.	잘렸다
유행성 이하선염	`#`	네.	아니요.	플로어
Netwide 어셈블러(NASM, NASMX)	`%`,`div`(설계 완료)	네.	아니요.	—
Netwide 어셈블러(NASM, NASMX)	`%%`(서명)	네.	아니요.	구현^[34] 정의
님	`mod`	네.	아니요.	잘렸다
오베론	`MOD`	네.	아니요.	플로어^[e] 같은
목표-C	`%`	네.	아니요.	잘림(C99와 동일)
오브젝트 파스칼, 델파이	`mod`	네.	아니요.	잘렸다
OCaml	`mod`	네.	아니요.	잘렸다^[35]
OCaml	`mod_float`	아니요.	네.	잘렸다^[36]
오캄	`\`	네.	아니요.	잘렸다
Pascal (ISO-7185 및 -10206)	`mod`	네.	아니요.	유클리드^[f] 같은
프로그래밍 코드 어드밴스드(PCA)	`\`	네.	아니요.	정의되어 있지 않다
펄	`%`	네.	아니요.	플로어^[g]
펄	`POSIX::fmod`	아니요.	네.	잘렸다
픽스	`mod`	네.	아니요.	플로어
픽스	`remainder`	네.	아니요.	잘렸다
PHP	`%`	네.	아니요.	잘렸다^[38]
PHP	`fmod`	아니요.	네.	잘렸다^[39]
PIC BASIC Pro	`\\`	네.	아니요.	잘렸다
PL/I	`mod`	네.	아니요.	플로어(ANSI PL/I)
PowerShell	`%`	네.	아니요.	잘렸다
프로그래밍 코드(PRC)	`MATH.OP - 'MOD; (\)'`	네.	아니요.	정의되어 있지 않다
진보.	`modulo`	네.	아니요.	잘렸다
프롤로그 (ISO 1995)	`mod`	네.	아니요.	플로어
프롤로그 (ISO 1995)	`rem`	네.	아니요.	잘렸다
Pure Basic	`%`,`Mod(x,y)`	네.	아니요.	잘렸다
PureScript	`mod`	네.	아니요.	유클리드^[40]
순수 데이터	`%`	네.	아니요.	잘림(C와 동일)
순수 데이터	`mod`	네.	아니요.	플로어
파이썬	`%`	네.	네.	플로어
파이썬	`math.fmod`	아니요.	네.	잘렸다
질문#	`%`	네.	아니요.	잘렸다^[41]
R	`%%`	네.	아니요.	플로어
라켓	`modulo`	네.	아니요.	플로어
라켓	`remainder`	네.	아니요.	잘렸다
라쿠	`%`	아니요.	네.	플로어
리얼 베이직	`MOD`	네.	아니요.	잘렸다
이유	`mod`	네.	아니요.	잘렸다
렉시	`//`	네.	네.	잘렸다
RPG	`%REM`	네.	아니요.	잘렸다
루비	`%`,`modulo()`	네.	네.	플로어
루비	`remainder()`	네.	네.	잘렸다
녹	`%`	네.	네.	잘렸다
녹	`rem_euclid()`	네.	네.	유클리드^[42]
SAS	`MOD`	네.	아니요.	잘렸다
스칼라	`%`	네.	아니요.	잘렸다
스킴	`modulo`	네.	아니요.	플로어
스킴	`remainder`	네.	아니요.	잘렸다
스킴 R⁶RS	`mod`	네.	아니요.	유클리드^[43]
	`mod0`	네.	아니요.	반올림^[43]
	`flmod`	아니요.	네.	유클리드
	`flmod0`	아니요.	네.	반올림
긁다	`mod`	네.	네.	플로어
시드7	`mod`	네.	네.	플로어
시드7	`rem`	네.	네.	잘렸다
센스톡	`modulo`	네.	아니요.	플로어
센스톡	`rem`	네.	아니요.	잘렸다
`sh` (POSIX) (bash, mksh 및 c 포함)	`%`	네.	아니요.	잘림(^[44]C와 동일)
스몰토크	`\\`	네.	아니요.	플로어
스몰토크	`rem:`	네.	아니요.	잘렸다
찰칵!	`mod`	네.	아니요.	플로어
스핀	`//`	네.	아니요.	플로어
솔리드티	`%`	네.	아니요.	플로어
SQL(SQL:1999)	`mod(x,y)`	네.	아니요.	잘렸다
SQL(SQL:2011)	`%`	네.	아니요.	잘렸다
표준 ML	`mod`	네.	아니요.	플로어
	`Int.rem`	네.	아니요.	잘렸다
	`Real.rem`	아니요.	네.	잘렸다
스타타	`mod(x,y)`	네.	아니요.	유클리드
재빠르다	`%`	네.	아니요.	잘렸다^[45]
	`remainder(dividingBy:)`	아니요.	네.	반올림^[46]
	`truncatingRemainder(dividingBy:)`	아니요.	네.	잘렸다^[47]
TCL	`%`	네.	아니요.	플로어
토크	`%`	네.	아니요.	잘렸다
튜링	`mod`	네.	아니요.	플로어
Verilog (2001)	`%`	네.	아니요.	잘렸다
VHDL	`mod`	네.	아니요.	플로어
VHDL	`rem`	네.	아니요.	잘렸다
VimL	`%`	네.	아니요.	잘렸다
비주얼 베이직	`Mod`	네.	아니요.	잘렸다
웹 어셈블리	`i32.rem_u`,`i64.rem_u`(설계 완료)	네.	아니요.	--^[48]
웹 어셈블리	`i32.rem_s`,`i64.rem_s`(서명)	네.	아니요.	잘렸다^[49]
x86 어셈블리	`IDIV`	네.	아니요.	잘렸다
XBase++	`%`	네.	네.	잘렸다
XBase++	`Mod()`	네.	네.	플로어
Z3 정리 프로버	`div`,`mod`	네.	아니요.	유클리드

게다가, 많은 컴퓨터 시스템들은divmod함수: 몫과 나머지를 동시에 생성합니다.예를 들어 x86 아키텍처는IDIV명령, C 프로그래밍 언어의div()기능 및 Python의divmod()기능.

일반화

오프셋이 있는 모듈로

때때로 모듈 $n$ 의 $결과$ 가 $0$ 과n - 1 사이에 있는 것이 아니라 $d$ 와d + n - $1$ $사이$ 에 있는 것이 유용합니다.이 경우 $d$ 를 오프셋이라고 합니다.이 조작에는 표준 표기법이 없는 것 같기 $때문$ 에_d mod n을 $시험적$ 으로 사용합니다.따라서 다음과 같은 ^[50]정의가 있습니다. d $x$ $x n d$ $d$ + n - $1$ 및 $x$ $mod$ n = $a$ $mod$ n인 경우 x = a mod n입니다.분명히 일반적인 모듈로 연산은 제로 오프셋에 해당합니다. $즉$ , $mod$ n = $mod 0$ n입니다.오프셋이 있는 모듈로의 작동은 다음과 같이 플로어 기능과 관련이 있습니다.

a\operatorname {mod}_{d}n=a-n\left\lfloor {frac {a-d}\right\loor

(이를 확인하려면 x ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ - ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ - ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ n ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ { $textstyle$ x = ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ a - n \ $lfloor$ \ $frac$ { a - $d }$ $\ right$ \ $loor$ 로 합니다. $먼저$ x $mod$ n = $a$ $mod$ n임을 나타냅니다.일반적으로 ( $a$ + $bn)$ $mod$ n = $모든$ $정수$ b에 대해 a $mod$ n이라는 것은 사실이다. 따라서 이는 ${\textstyle b=-\!\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ ${\textstyle b=-\!\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ - ${\textstyle b=-\!\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ ⌊ ${\textstyle b=-\!\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ - ${\textstyle b=-\!\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ ${\textstyle b=-\!\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ ${\$ { $textstyle$ b $=$ - \ ! $\left\lfloor$ { $frac {a-d}{n$ right $\$ ${\textstyle x{\bmod {n}}=\left(a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor \right)\!{\bmod {n}}=a{\bmod {n}}}$ ${\textstyle b=-\!\left\lfloor {\frac {a-d}{n}}\right\rfloor }$ = a ${\textstyle x{\bmod {n}}=\left(a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor \right)\!{\bmod {n}}=a{\bmod {n}}}$ - ${\textstyle x{\bmod {n}}=\left(a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor \right)\!{\bmod {n}}=a{\bmod {n}}}$ ${\textstyle x{\bmod {n}}=\left(a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor \right)\!{\bmod {n}}=a{\bmod {n}}}$ ${\textstyle x{\bmod {n}}=\left(a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor \right)\!{\bmod {n}}=a{\bmod {n}}}$ ${\textstyle x{\bmod {n}}=\left(a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor \right)\!{\bmod {n}}=a{\bmod {n}}}$ \ $textstyle x440bmod {$ n} = \ $left$ ( a - $n$ \ $left$ \ $lfloor$ { $frac$ { - d ${\textstyle x{\bmod {n}}=\left(a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor \right)\!{\bmod {n}}=a{\bmod {n}}}$ { n } { n } } \right \ $loor$ a - n $that$ ${\textstyle x{\bmod {n}}=\left(a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor \right)\!{\bmod {n}}=a{\bmod {n}}}$ that that that that that that that that that that that that that that that that that that that that that that that that that that that that that that that that that that that thatrightrightrightrightright $({bmod$ { $n}}=a440bmod$ {n ${\textstyle x{\bmod {n}}=\left(a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor \right)\!{\bmod {n}}=a{\bmod {n}}}$ 증명하고 싶었던 것입니다 $.$ $d x$ x $d$ d + $n$ - $1$ . k와 $r$ 이0 $r$ r $\leq n$ - $1인 정수$ 라고 $하자$ (유클리드 나눗셈 참조). ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ 으로 ${\textstyle \left\lfloor {\frac {a-d}{n}}\right\rfloor =k}$ a ${\textstyle \left\lfloor {\frac {a-d}{n}}\right\rfloor =k}$ - ${\textstyle \left\lfloor {\frac {a-d}{n}}\right\rfloor =k}$ ${\textstyle \left\lfloor {\frac {a-d}{n}}\right\rfloor =k}$ \ $textstyle \ lfloor$ \ $frac$ { a - ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ $}$ \ $right$ \ $loor$ ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ $k$ ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ d ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ + ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ \ $text style$ x = ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ a - ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ \ $lfloor$ \ $frac$ { a - d } \ loor { fright \ ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ { a - n ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ a - n ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ a - ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ n a a ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ a n a n a then then then then then a a a then = a - n ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ d $then$ n ${\textstyle x=a-n\left\lfloor {\frac {a-d}{n}}\right\rfloor =a-nk=d+r}$ n then n 。이제 0 ≤ $r - n$ - 1을 $취해서$ 양변에 d를 $더하면$ d $r d$ + r $d$ + n - 1을 $얻을$ 수 있습니다. 하지만 $x =$ $d$ + r인 $것$ 을 확인했으므로, 이것으로 끝입니다.□)

$오프셋$ 이 mod $n$ 인_d modulo는 Mathematica에서 다음과 같이 구현됩니다.Mod[a, n, d]를 클릭합니다.^[50]

절단을 사용하여 다른 모듈로 정의 구현

크누스의 층분할과 유클리드 나눗셈의 수학적 우아함에도 불구하고, 일반적으로 프로그래밍 언어에서 잘린 나눗셈 기반의 모듈을 찾는 것이 훨씬 더 흔하다.레이젠은 잘린 정수 ^[5]나눗셈이 주어진 두 나눗셈을 계산하기 위해 다음과 같은 알고리즘을 제공합니다.

/* 유클리드 및 플로어 divmod, C의 ldiv() 스타일 */ 유형화된 구조 {   /* 이 구조는 C stdlib.h의 일부이지만 명확성을 위해 여기서 재현됩니다.* /   긴 인트 견적서;   긴 인트 기억하다; } ldiv_t;  /* 유클리드 나눗셈 */ 인라인 ldiv_t ldivE(긴 넘버전, 긴 분파) {   /* C99 언어 및 C++11 언어에서는 둘 다 잘라내기 언어라고 정의합니다.*/   긴 q = 넘버전 / 분파;   긴 r = 넘버전 % 분파;   한다면 (r < > 0) {     한다면 (분파 > 0) {       q = q - 1;       r = r + 분파;     } 또 다른 {       q = q + 1;       r = r - 분파;     }   }   돌아가다 (ldiv_t){.견적서 = q, .기억하다 = r}; }  /* 플로어 부문 */ 인라인 ldiv_t ldivF(긴 넘버전, 긴 분파) {   긴 q = 넘버전 / 분파;   긴 r = 넘버전 % 분파;   한다면 ((r > 0 & & 분파 < > 0)    (r < > 0 & & 분파 > 0)) {     q = q - 1;     r = r + 분파;   }   돌아가다 (ldiv_t){.견적서 = q, .기억하다 = r}; }

두 경우 모두 나머지는 지수와 독립적으로 계산할 수 있지만 그 반대는 아닙니다.논리 브런치가 같기 때문에 화면 공간을 절약하기 위해 여기서 작업이 결합됩니다.

「」를 참조해 주세요.

Modulo(동음이의 설명)와 Modulo(jargon) – Modulo라는 단어의 많은 사용은 Carl F에서 비롯되었습니다. 1801년 가우스의 모듈식 산술 도입.
모듈로(수학), 수학에서 일반적으로 사용되는 용어
모듈러형 지수화
턴(단위)

메모들

^ 수학적으로, 이 두 가지 선택은 나머지가 만족하는 부등식에서 사용할 수 있는 무한한 수의 선택 중 두 개에 불과합니다.
^ ^a ^b 인수의 순서가 반대로 되어 있다.α ω $\omega {\bmod {\alpha }}$ mod $\omega {\bmod {\alpha }}$ \ $displaystyle \ obmod$ \ $alpha }$ 를 계산합니다.나머지는 나눗셈 시입니다.ω타고α.
^ C99 및 C++11은 다음 동작을 정의합니다.%잘립니다.^[9]그 이전의 표준에서는 동작의 실장이 ^[10]정의되어 있습니다.
^ ACUCOBOL, Micro Focus COBOL 및 가능한 기타에 구현되어 있습니다.
^ 제수는 양수여야 하며, 그렇지 않으면 정의되지 않아야 합니다.
^ Boute에서 논의한 바와 같이 ISO Pascal의 정의는 다음과 같습니다.div그리고.modD $= d$ · ( $D / d)$ + $D$ % $d$ 의 나눗셈 동일성을 따르지 않으므로 근본적으로 파손된다.
^ Perl은 일반적으로 머신에 의존하지 않는 산술 모듈로 연산자를 사용합니다.예와 예외에 대해서는 곱셈 ^[37]연산자에 관한 Perl 문서를 참조하십시오.

레퍼런스

^ Weisstein, Eric W. "Congruence". mathworld.wolfram.com. Retrieved 2020-08-27.
^ Caldwell, Chris. "residue". Prime Glossary. Retrieved August 27, 2020.
^ Knuth, Donald. E. (1972). The Art of Computer Programming. Addison-Wesley.
^ Boute, Raymond T. (April 1992). "The Euclidean definition of the functions div and mod". ACM Transactions on Programming Languages and Systems. ACM Press (New York, NY, USA). 14 (2): 127–144. doi:10.1145/128861.128862. hdl:1854/LU-314490. S2CID 8321674.
^ ^a ^b Leijen, Daan (December 3, 2001). "Division and Modulus for Computer Scientists" (PDF). Retrieved 2014-12-25. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
^ Peterson, Doctor (5 July 2001). "Mod Function and Negative Numbers". Math Forum - Ask Dr. Math. Archived from the original on 2019-10-22. Retrieved 22 October 2019.
^ Horvath, Adam (July 5, 2012). "Faster division and modulo operation - the power of two".
^ ^a ^b "ISO/IEC 8652:2012 - Information technology — Programming languages — Ada". ISO, IEC. 2012. sec. 4.5.5 Multiplying Operators. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
^ "C99 specification (ISO/IEC 9899:TC2)" (PDF). 2005-05-06. sec. 6.5.5 Multiplicative operators. Retrieved 16 August 2018.
^ "ISO/IEC 14882:2003: Programming languages – C++". International Organization for Standardization (ISO), International Electrotechnical Commission (IEC). 2003. sec. 5.6.4. the binary % operator yields the remainder from the division of the first expression by the second. .... If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
^ "ISO/IEC 9899:1990: Programming languages – C". ISO, IEC. 1990. sec. 7.5.6.4. The $fmod$ function returns the value $x - i * y$ , for some integer $i$ such that, if $y$ is nonzero, the result has the same sign as $x$ and magnitude less than the magnitude of $y$ . {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
^ "clojure.core - Clojure v1.10.3 API documentation". clojure.github.io. Retrieved 2022-03-16.
^ "clojure.core - Clojure v1.10.3 API documentation". clojure.github.io. Retrieved 2022-03-16.
^ CoffeeScript 연산자
^ "Expressions - D Programming Language". dlang.org. Retrieved 2021-06-01.
^ "operator % method - num class - dart:core library - Dart API". api.dart.dev. Retrieved 2021-06-01.
^ "remainder method - num class - dart:core library - Dart API". api.dart.dev. Retrieved 2021-06-01.
^ "Kernel — Elixir v1.11.3". hexdocs.pm. Retrieved 2021-01-28.
^ "Integer — Elixir v1.11.3". hexdocs.pm. Retrieved 2021-01-28.
^ "Basics - core 1.0.5". package.elm-lang.org. Retrieved 2022-03-16.
^ "Basics - core 1.0.5". package.elm-lang.org. Retrieved 2022-03-16.
^ "Erlang -- math". erlang.org. Retrieved 2021-06-01.
^ "GLSL Language Specification, Version 4.50.7" (PDF). section 5.9 Expressions. If both operands are non-negative, then the remainder is non-negative. Results are undefined if one or both operands are negative.
^ "GLSL Language Specification, Version 4.50.7" (PDF). section 8.3 Common Functions.
^ "The Go Programming Language Specification - The Go Programming Language". go.dev. Retrieved 2022-02-28.
^ "math package - math - pkg.go.dev". pkg.go.dev. Retrieved 2022-02-28.
^ "big package - math/big - pkg.go.dev". pkg.go.dev. Retrieved 2022-02-28.
^ ^a ^b "6 Predefined Types and Classes". www.haskell.org. Retrieved 2022-05-22.
^ "Operators". Microsoft. Retrieved 2021-07-19. The % operator is defined only in cases where either both sides are positive or both sides are negative. Unlike C, it also operates on floating-point data types, as well as integers.
^ "Mathematics · The Julia Language". docs.julialang.org. Retrieved 2021-11-20.
^ "Mathematics · The Julia Language". docs.julialang.org. Retrieved 2021-11-20.
^ "rem - Kotlin Programming Language". Kotlin. Retrieved 2021-05-05.
^ "mod - Kotlin Programming Language". Kotlin. Retrieved 2021-05-05.
^ "Chapter 3: The NASM Language". NASM - The Netwide Assembler version 2.15.05.
^ "OCaml library : Stdlib". ocaml.org. Retrieved 2022-02-19.
^ "OCaml library : Stdlib". ocaml.org. Retrieved 2022-02-19.
^ Perl 문서
^ "PHP: Arithmetic Operators - Manual". www.php.net. Retrieved 2021-11-20.
^ "PHP: fmod - Manual". www.php.net. Retrieved 2021-11-20.
^ "EuclideanRing".
^ QuantumWriter. "Expressions". docs.microsoft.com. Retrieved 2018-07-11.
^ "F32 - Rust".
^ ^a ^b r6rs.org
^ "Shell Command Language". pubs.opengroup.org. Retrieved 2021-02-05.
^ "Apple Developer Documentation". developer.apple.com. Retrieved 2021-11-20.
^ "Apple Developer Documentation". developer.apple.com. Retrieved 2021-11-20.
^ "Apple Developer Documentation". developer.apple.com. Retrieved 2021-11-20.
^ "Numerics — WebAssembly 1.1 (Draft 2022-03-02)". webassembly.github.io. Retrieved 2022-03-16.
^ "Numerics — WebAssembly 1.1 (Draft 2022-03-02)". webassembly.github.io. Retrieved 2022-03-16.
^ ^a ^b "Mod". Wolfram Language & System Documentation Center. Wolfram Research. 2020. Retrieved April 8, 2020.

외부 링크

모듈로라마, 곱셈표의 주기적 표현 애니메이션(프랑스어 설명)

[3] 수학적으로, 이 두 가지 선택은 나머지가 만족하는 부등식에서 사용할 수 있는 무한한 수의 선택 중 두 개에 불과합니다.

[rev-10] 인수의 순서가 반대로 되어 있다.α ω $\omega {\bmod {\alpha }}$ mod $\omega {\bmod {\alpha }}$ \ $displaystyle \ obmod$ \ $alpha }$ 를 계산합니다.나머지는 나눗셈 시입니다.ω타고α.

[c-13] C99 및 C++11은 다음 동작을 정의합니다.%잘립니다.^[9]그 이전의 표준에서는 동작의 실장이 ^[10]정의되어 있습니다.

[17] ACUCOBOL, Micro Focus COBOL 및 가능한 기타에 구현되어 있습니다.

[39] 제수는 양수여야 하며, 그렇지 않으면 정의되지 않아야 합니다.

[42] Boute에서 논의한 바와 같이 ISO Pascal의 정의는 다음과 같습니다.div그리고.modD $= d$ · ( $D / d)$ + $D$ % $d$ 의 나눗셈 동일성을 따르지 않으므로 근본적으로 파손된다.

[44] Perl은 일반적으로 머신에 의존하지 않는 산술 모듈로 연산자를 사용합니다.예와 예외에 대해서는 곱셈 ^[37]연산자에 관한 Perl 문서를 참조하십시오.

[1] Weisstein, Eric W. "Congruence". mathworld.wolfram.com. Retrieved 2020-08-27.

[2] Caldwell, Chris. "residue". Prime Glossary. Retrieved August 27, 2020.

[4] Knuth, Donald. E. (1972). The Art of Computer Programming. Addison-Wesley.

[5] Boute, Raymond T. (April 1992). "The Euclidean definition of the functions div and mod". ACM Transactions on Programming Languages and Systems. ACM Press (New York, NY, USA). 14 (2): 127–144. doi:10.1145/128861.128862. hdl:1854/LU-314490. S2CID 8321674.

[Leijen-6] Leijen, Daan (December 3, 2001). "Division and Modulus for Computer Scientists" (PDF). Retrieved 2014-12-25. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)

[7] Peterson, Doctor (5 July 2001). "Mod Function and Negative Numbers". Math Forum - Ask Dr. Math. Archived from the original on 2019-10-22. Retrieved 22 October 2019.

[8] Horvath, Adam (July 5, 2012). "Faster division and modulo operation - the power of two".

[Ada-9] "ISO/IEC 8652:2012 - Information technology — Programming languages — Ada". ISO, IEC. 2012. sec. 4.5.5 Multiplying Operators. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)

[C99-11] "C99 specification (ISO/IEC 9899:TC2)" (PDF). 2005-05-06. sec. 6.5.5 Multiplicative operators. Retrieved 16 August 2018.

[12] "ISO/IEC 14882:2003: Programming languages – C++". International Organization for Standardization (ISO), International Electrotechnical Commission (IEC). 2003. sec. 5.6.4. the binary % operator yields the remainder from the division of the first expression by the second. .... If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)

[14] "ISO/IEC 9899:1990: Programming languages – C". ISO, IEC. 1990. sec. 7.5.6.4. The $fmod$ function returns the value $x - i * y$ , for some integer $i$ such that, if $y$ is nonzero, the result has the same sign as $x$ and magnitude less than the magnitude of $y$ . {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)

[15] "clojure.core - Clojure v1.10.3 API documentation". clojure.github.io. Retrieved 2022-03-16.

[16] "clojure.core - Clojure v1.10.3 API documentation". clojure.github.io. Retrieved 2022-03-16.

[CoffeeScript-18] CoffeeScript 연산자

[19] "Expressions - D Programming Language". dlang.org. Retrieved 2021-06-01.

[20] "operator % method - num class - dart:core library - Dart API". api.dart.dev. Retrieved 2021-06-01.

[21] "remainder method - num class - dart:core library - Dart API". api.dart.dev. Retrieved 2021-06-01.

[22] "Kernel — Elixir v1.11.3". hexdocs.pm. Retrieved 2021-01-28.

[23] "Integer — Elixir v1.11.3". hexdocs.pm. Retrieved 2021-01-28.

[24] "Basics - core 1.0.5". package.elm-lang.org. Retrieved 2022-03-16.

[25] "Basics - core 1.0.5". package.elm-lang.org. Retrieved 2022-03-16.

[26] "Erlang -- math". erlang.org. Retrieved 2021-06-01.

[27] "GLSL Language Specification, Version 4.50.7" (PDF). section 5.9 Expressions. If both operands are non-negative, then the remainder is non-negative. Results are undefined if one or both operands are negative.

[28] "GLSL Language Specification, Version 4.50.7" (PDF). section 8.3 Common Functions.

[29] "The Go Programming Language Specification - The Go Programming Language". go.dev. Retrieved 2022-02-28.

[30] "math package - math - pkg.go.dev". pkg.go.dev. Retrieved 2022-02-28.

[31] "big package - math/big - pkg.go.dev". pkg.go.dev. Retrieved 2022-02-28.

[Haskell_2010-32] "6 Predefined Types and Classes". www.haskell.org. Retrieved 2022-05-22.

[33] "Operators". Microsoft. Retrieved 2021-07-19. The % operator is defined only in cases where either both sides are positive or both sides are negative. Unlike C, it also operates on floating-point data types, as well as integers.

[34] "Mathematics · The Julia Language". docs.julialang.org. Retrieved 2021-11-20.

[35] "Mathematics · The Julia Language". docs.julialang.org. Retrieved 2021-11-20.

[36] "rem - Kotlin Programming Language". Kotlin. Retrieved 2021-05-05.

[37] "mod - Kotlin Programming Language". Kotlin. Retrieved 2021-05-05.

[38] "Chapter 3: The NASM Language". NASM - The Netwide Assembler version 2.15.05.

[40] "OCaml library : Stdlib". ocaml.org. Retrieved 2022-02-19.

[41] "OCaml library : Stdlib". ocaml.org. Retrieved 2022-02-19.

[43] Perl 문서

[45] "PHP: Arithmetic Operators - Manual". www.php.net. Retrieved 2021-11-20.

[46] "PHP: fmod - Manual". www.php.net. Retrieved 2021-11-20.

[purescript_euclid-47] "EuclideanRing".

[48] QuantumWriter. "Expressions". docs.microsoft.com. Retrieved 2018-07-11.

[rust_rem_euclid-49] "F32 - Rust".

[r6rs-50] r6rs.org

[51] "Shell Command Language". pubs.opengroup.org. Retrieved 2021-02-05.

[52] "Apple Developer Documentation". developer.apple.com. Retrieved 2021-11-20.

[53] "Apple Developer Documentation". developer.apple.com. Retrieved 2021-11-20.

[54] "Apple Developer Documentation". developer.apple.com. Retrieved 2021-11-20.

[55] "Numerics — WebAssembly 1.1 (Draft 2022-03-02)". webassembly.github.io. Retrieved 2022-03-16.

[56] "Numerics — WebAssembly 1.1 (Draft 2022-03-02)". webassembly.github.io. Retrieved 2022-03-16.

[Mathematica_Mod-57] "Mod". Wolfram Language & System Documentation Center. Wolfram Research. 2020. Retrieved April 8, 2020.

[1]

[2]

[a]

[3]

[4]

[6]

[7]

[8]

[b]

[c]

[11]

[12]

[13]

[d]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[e]

[35]

[36]

[f]

[g]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[5]

[9]

[10]

[37]

Search

모듈로 연산

네임스페이스

더

목차

정의의 변형

표기법

일반적인 함정

퍼포먼스 문제

속성(아이덴티티)

프로그래밍 언어

일반화

오프셋이 있는 모듈로

절단을 사용하여 다른 모듈로 정의 구현

「」를 참조해 주세요.

메모들

레퍼런스

외부 링크

Search

모듈로 연산

정의의 변형

표기법

일반적인 함정

퍼포먼스 문제

속성(아이덴티티)

프로그래밍 언어

일반화

오프셋이 있는 모듈로

절단을 사용하여 다른 모듈로 정의 구현

「 」를 참조해 주세요.

메모들

레퍼런스

외부 링크

「」를 참조해 주세요.