최대 길이 시퀀스

최대 길이 시퀀스(MLS)는 유사 항만두 시퀀스의 한 유형이다.

그것들은 최대 선형 피드백 시프트 레지스터를 사용하여 생성된 비트 시퀀스인데, 이들은 주기적이며 시프트 레지스터로 나타낼 수 있는 모든 이진 시퀀스(영점 벡터 제외)를 재현하기 때문에 그렇게 불린다(즉, 길이-m 레지스터의 경우^m 길이 2 - 1의 시퀀스를 생성한다). MLS는 n-시퀀스 또는 m-시퀀스라고도 불린다. MLS는 거의 0 DC 항을 제외하고 놀랄 만큼 평평하다.

이러한 시퀀스는 Z/2Z를 통한 다항식 링에서 수정 불가능한 다항식 계수로 나타낼 수 있다.

MLS에 대한 실제 적용은 충동 반응 측정(예: 실내 반향)을 포함한다. 그것들은 또한 직접 시퀀스 확산 스펙트럼과 주파수 호핑 확산 스펙트럼 전송 시스템, 광학적 유전체 다층 반사체 설계 ^[1]및 일부 fMRI 실험의 효율적인 설계에서 사이비 무작위 시퀀스를 도출하는 기초로서 사용된다.^[2]

세대

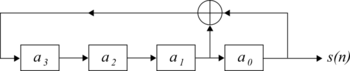
그림 1: 길이 4의 피드백 시프트 레지스터에서 a₃ 레지스터의 다음 값은 a와₀ a의₁ modulo-2 합계에 의해 결정된다.

MLS는 최대 선형 피드백 시프트 레지스터를 사용하여 생성된다. 길이 4의 변속 레지스터를 가진 MLS 생성 시스템은 그림 1과 같다. 다음과 같은 재귀적 관계를 사용하여 표현할 수 있다.

{\displaysty}a_{3}[n+1]=a_{0}[n]+a_{1]}[n]\\a_{2}[n+1]=a_{3}[n]\\a_{1}[n+1]=a_{2}[n]\a_{0}[n+1]=a_{1}}=a_{1}[n]\case{1}}}}}}

여기서 n은 시간 색인이고 $+$ + $+$ 은 modulo-2 추가를 나타낸다 $+$ . 비트 값 0 = FALSE 또는 1 = TRUE의 경우 이는 XOR 연산과 동일하다.

MLS는 주기적이며 가능한 모든 이진수 값(영점 벡터 제외)을 통하여 시프트 레지스터를 주기 때문에, 레지스터는 영점 벡터를 제외하고 어떤 상태로도 초기화할 수 있다.

다항해석

GF(2)를 통한 다항식은 선형 피드백 시프트 레지스터와 연관될 수 있다. 시프트 레지스터의 길이 정도를 가지며, xor 게이트를 공급하는 레지스터의 탭과 일치하는 0 또는 1의 계수를 가진다. 예를 들어 그림 1에 해당하는 다항식은 x⁴ + x + 1이다¹.

LFSR에 의해 생성된 시퀀스가 최대 길이가 되도록 하기 위해 필요하고 충분한 조건은 해당 다항식이 원시적이라는 것이다.^[3]

실행

MLS는 하드웨어 또는 소프트웨어에서 구현하는 비용이 저렴하며 상대적으로 저차 피드백 시프트 레지스터는 긴 시퀀스를 생성할 수 있다. 길이 20의 시프트 레지스터를 사용하여 생성된 시퀀스는 2²⁰ - 1 샘플 길이(1,048,575 샘플)이다.

최대 길이 시퀀스의 속성

MLS는 솔로몬 골롬이 공식화한 다음과 같은 성질을 가지고 있다.^[4]

잔액재산

시퀀스에서 0과 1의 발생은 거의 동일해야 한다. 보다 정확히 말하면, 길이 $2^{n}-1$ - 1 ${\displaystyle$ 2 $^{n1}-1$ 의 최대 길이 순서에는 $2^{n-1}$ - $2^{n-1}$ ${\$ 2 $^{n-1}$ 0과 $2^{n-1}-1$ - ${\displaystyle$ 2 $^{n-1}-1}$ 의 $2^{n-1}$ $2^{n-1}-1$ 0이 있다 $2^{n}-1$ . 0만 포함하는 상태는 발생할 수 없으므로 1의 수는 0에 1을 더한 값과 같다.

속성 실행

"실행"은 해당 MLS 내에서 연속 "1" 또는 연속 "0"의 하위 시퀀스다. 런 수는 그러한 하위 시퀀스의 수입니다.^[vague]

시퀀스의 모든 "런"( "1" 또는 "0"으로 구성됨) 중에서 다음 중 하나를 선택하십시오.

런의 절반은 길이 1이다.
주행의 4분의 1은 길이 2이다.
달리기의 8분의 1은 길이 3이다.
… 등...

상관 속성

MLS의 순환 자기 상관은 크로네커 델타 함수^[5]^[6](실행 여부에 따라 DC 오프셋 및 시간 지연 포함)이다. ±1 규칙의 경우, 즉 비트 값 $s=+1$ 은 $s=+1$ = $s=+1$ + 1 ${\displaystyle$ s $=+1},$ 비트 $s=+1$ 값 0 $s=-1$ = $s=-1$ - 1 ${\displaystyle$ s $=-1$ XOR을 제품의 음수에 매핑한다.

$R(n)={\frac {1}{{N}\sum _{m=1}^{{N}s[m]\,s^{*}[m+n]_{{{{N}s]N}={\begin{case}1&{\text}{{}n=0,\-{\frac {1}{{N}&{\text{}}{}}{{}}n.\end{case}}$

여기서 $∗{\$ 는 복합 결합을 나타내며 $s^{*}$ $[m+n]_{N}$ [ $[m+n]_{N}$ + $[m+n]_{N}$ ] $[m+n]_{N}$ {\ $displaystyle [m+n]_$ ${{N}}$ 은 $[m+n]_{N}$ 원형 교대조를 나타낸다.

MLS의 선형 자기 상관은 Kronecker 델타에 가깝다.

임펄스 반응 추출

LTI(Linear time invariant) 시스템의 임펄스 응답을 MLS로 측정하려면 MLS와 원형 교차 상관 관계를 취하여 측정된 시스템 출력 y[n]에서 응답을 추출할 수 있다. 이는 MLS의 자기 상관은 제로래그에 대해 1이고, 다른 모든 시차에는 거의 0(-1/N, 여기서 N은 시퀀스 길이)이기 때문이다. 즉, MLS의 자기 상관은 MLS 길이가 증가함에 따라 단위 임펄스 기능에 접근한다고 말할 수 있다.

시스템의 임펄스 반응이 h[n]이고 MLS가 s[n]이면,

[\displaystyle y[n]=(h*s)[n]\,}

양쪽의 의견이 서로 엇갈리는 것을 보면,

{\phi }_{sy}=h[n]*{\phi }_{ss}\,

그리고 φ이_ss 충동이라고 가정한다(긴 시퀀스에 유효함)

h[n]={\phi }_{sy}\,

충동 자기 상관을 가진 어떤 신호도 이를 위해 사용할 수 있지만, 충동 자체와 같이 파고율이 높은 신호는 신호 대 잡음 비율이 낮은 충동 반응을 일으킨다. 일반적으로 MLS는 풀 스케일 값으로만 구성되며 디지털 파고율은 최소값인 0dB이므로 이상적인 신호가 될 것으로 가정한다.^[7]^[8] 그러나 아날로그 재구성 후 신호의 급격한 불연속은 강한 샘플 간 피크를 생성하여 파고율을 4-8dB 이상 떨어뜨리고 신호 길이에 따라 증가시켜 사인 스위프보다 더 악화된다.^[9] 다른 신호는 3dB 이상으로 개선할 수 있을지는 알 수 없지만 최소한의 파고율로 설계되었다.^[10]

Hadamard 변환과의 관계

쿤과 렘펠은^[11] MLS와 하다마드 변형과의 관계를 보여주었다. 이 관계를 통해 MLS의 상관관계를 FFT와 유사한 고속 알고리즘으로 계산할 수 있다.

참고 항목

참조

Golomb, Solomon W.; Guang Gong (2005). Signal Design for Good Correlation: For Wireless Communication, Cryptography, and Radar. Cambridge University Press. ISBN 978-0-521-82104-9.

^ Poudel, Khem Narayan; Robertson, William M. (2018-10-15). "Maximum length sequence dielectric multilayer reflector". OSA Continuum. 1 (2): 358–372. doi:10.1364/OSAC.1.000358. ISSN 2578-7519.
^ Buracas GT, Boynton GM (July 2002). "Efficient design of event-related fMRI experiments using M-sequences". NeuroImage. 16 (3 Pt 1): 801–13. doi:10.1006/nimg.2002.1116. PMID 12169264.
^ "선형 피드백 시프트 레지스터-이행, M-시퀀스 속성, 피드백 표"[1], New Wave Instruments(NW), Retried 2013.12.03.
^ Golomb, Solomon W. (1967). Shift register sequences. Holden-Day. ISBN 0-89412-048-4.
^ Jacobsen, Finn; Juhl, Peter Moller (2013-06-04). Fundamentals of General Linear Acoustics. John Wiley & Sons. ISBN 978-1118636176. A maximum-length sequence is a binary sequence whose circular autocorrelation (except for a small DC-error) is a delta function.
^ Sarwate, D. V.; Pursley, M. B. (1980-05-01). "Crosscorrelation properties of pseudorandom and related sequences". Proceedings of the IEEE. 68 (5): 593–619. doi:10.1109/PROC.1980.11697. ISSN 0018-9219.
^ "A Little MLS (Maximum-Length Sequence) Tutorial dspGuru.com". dspguru.com. Retrieved 2016-05-19. its RMS and peak values are both X, making its crest factor (peak/RMS) equal to 1, the lowest it can get.
^ "Other Electro-Acoustical Measurement Techniques". www.clear.rice.edu. Retrieved 2016-05-19. The crest factor for MLS is very close to 1, so it makes sense to use this kind of input signal when we need a high signal-to-noise ratio for our measurement
^ Chan, Ian H. "Swept Sine Chirps for Measuring Impulse Response" (PDF). thinksrs.com. Retrieved 2016-05-19.
^ Friese, M. (1997-10-01). "Multitone signals with low crest factor" (PDF). IEEE Transactions on Communications. 45 (10): 1338–1344. doi:10.1109/26.634697. ISSN 0090-6778.
^ Cohn, M.; Lempel, A. (January 1977). "On Fast M-Sequence Transforms". IEEE Trans. Inf. Theory. 23 (1): 135–7. doi:10.1109/TIT.1977.1055666.

외부 링크

Bristow-Johnson, Robert. "A Little MLS Tutorial". — 선형 시간 변화 시스템의 충동 응답을 얻기 위해 MLS를 사용하는 방법을 설명하는 짧은 온라인 자습서. 또한 시스템의 비선형성이 명백한 충동 반응에서 허위 스파이크로 나타날 수 있는 방법도 설명한다.
Hee, Jens. "Impulse response measurement using MLS" (PDF). — MLS 생성을 설명하는 용지. 최대 18-tap-LFSR을 사용하는 MLS 생성을 위한 C-code와 임펄스 반응 추출에 일치하는 Hadamard 변환 포함.
Kerr, Wesley; Drucker, Daniel. "Creation of M-Sequences". Geoffrey Aguirre Lab. University of Pennsylvania.
"Linear Feedback Shift Registers". New Wave Instruments. 2005. — 7 ~ 16,777,215(3 ~ 24 단계)의 최대 길이에 대한 최대 길이 시퀀스 속성 및 포괄적인 피드백 표, 최대 길이 4,294,967,295(25 ~ 32 단계)의 부분 표.
Schäfer, Magnus (October 2012). "Aachen Impulse Response Database". Institute of Communication Systems and Data Processing, RWTH Aachen University. V1.4. 최대 길이 시퀀스를 통해 생성된 (양방향) 실내 충격 응답 데이터베이스.
"Efficient Shift Registers, LFSR Counters, and Long Pseudo-Random Sequence Generators — Obsolete" (PDF). Xilinx. July 1996. XAPP052 v1.1. — FPGA에서 lfsr 구현에는 3 ~ 168비트의 탭 목록이 포함됨

[1] Poudel, Khem Narayan; Robertson, William M. (2018-10-15). "Maximum length sequence dielectric multilayer reflector". OSA Continuum. 1 (2): 358–372. doi:10.1364/OSAC.1.000358. ISSN 2578-7519.

[buracas-2] Buracas GT, Boynton GM (July 2002). "Efficient design of event-related fMRI experiments using M-sequences". NeuroImage. 16 (3 Pt 1): 801–13. doi:10.1006/nimg.2002.1116. PMID 12169264.

[3] "선형 피드백 시프트 레지스터-이행, M-시퀀스 속성, 피드백 표"[1], New Wave Instruments(NW), Retried 2013.12.03.

[golumb-4] Golomb, Solomon W. (1967). Shift register sequences. Holden-Day. ISBN 0-89412-048-4.

[5] Jacobsen, Finn; Juhl, Peter Moller (2013-06-04). Fundamentals of General Linear Acoustics. John Wiley & Sons. ISBN 978-1118636176. A maximum-length sequence is a binary sequence whose circular autocorrelation (except for a small DC-error) is a delta function.

[6] Sarwate, D. V.; Pursley, M. B. (1980-05-01). "Crosscorrelation properties of pseudorandom and related sequences". Proceedings of the IEEE. 68 (5): 593–619. doi:10.1109/PROC.1980.11697. ISSN 0018-9219.

[7] "A Little MLS (Maximum-Length Sequence) Tutorial dspGuru.com". dspguru.com. Retrieved 2016-05-19. its RMS and peak values are both X, making its crest factor (peak/RMS) equal to 1, the lowest it can get.

[8] "Other Electro-Acoustical Measurement Techniques". www.clear.rice.edu. Retrieved 2016-05-19. The crest factor for MLS is very close to 1, so it makes sense to use this kind of input signal when we need a high signal-to-noise ratio for our measurement

[9] Chan, Ian H. "Swept Sine Chirps for Measuring Impulse Response" (PDF). thinksrs.com. Retrieved 2016-05-19.

[10] Friese, M. (1997-10-01). "Multitone signals with low crest factor" (PDF). IEEE Transactions on Communications. 45 (10): 1338–1344. doi:10.1109/26.634697. ISSN 0090-6778.

[cohn-11] Cohn, M.; Lempel, A. (January 1977). "On Fast M-Sequence Transforms". IEEE Trans. Inf. Theory. 23 (1): 135–7. doi:10.1109/TIT.1977.1055666.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

Search