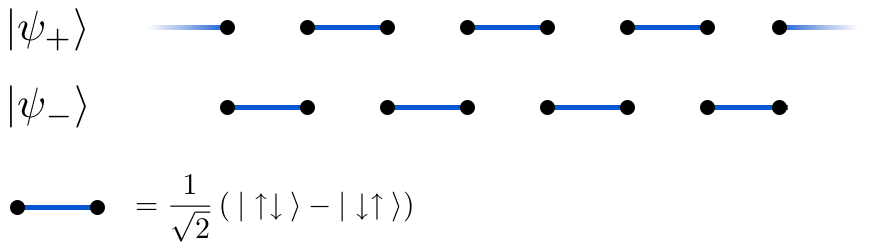마줌다-고시 모형

마줌다-고시 모델은 1차원 양자 하이젠베르크 스핀 모델로, 가장 가까운 이웃의 반강자성 교환 상호작용이 다음 이웃의 상호작용보다 두 배 더 강하다. $J_{1}$ $J_{1}=2J_{2}$ 인 $({$ - $({$ $J_$ ${2})$ 모델의 $J_{2}$ 특수한 케이스이며, J1 $=$ $J_{1}=2J_{2}$ $({$ }= $2J_{2$ $J_{1}=2J_{2}$ 입니다.이 모델의 이름은 인도의 물리학자 찬찰 쿠마르 마줌다와 디판 ^[1]고쉬의 이름을 따왔다.

마줌다-고시 모델은 지면 상태(최저 에너지 양자 상태)를 정확하게 찾아 간단한 형태로 작성할 수 있어 보다 복잡한 스핀 모델과 위상을 이해하는 데 유용한 출발점이 되기 때문에 주목할 만하다.

정의.

마줌다-고시 모델은 다음 해밀턴에 의해 정의된다.

{H}=J\sum _{j=1}^{N}{\vec {S}_{j}\cdot {S}_{j+1}+{{2}}\sum _{J=1}^{N}{\ve {S}{cdVE {C}S}{\cdVE {\cd

여기서 S 벡터는 양자수 S = 1/2인 양자 스핀 연산자이다.

계수에 대한 다른 규칙은 문헌에서 채택될 수 있지만, 가장 중요한 사실은 첫째 이웃과 둘째 이웃의 커플링의 비율이 2:1이라는 것이다.이 비율의 결과로, 해밀턴(전체 상수에 의해 이동)을 다음과 같이 동등하게 표현할 수 있다.

({displaystyle {H}}={j=1}^{N}({\vec {S}}_{j1}+{\vec {S}_{j}+{\vec {S}_{j+1}}^2})

합계량은 다름 아닌 3개의 연속된 $j-1,j,j+1$ j - $j-1,j,j+1$ , $j-1,j,j+1$ , $j-1,j,j+1$ j + $j-1,j,j+1$ ({ $displaystyle j-1, j$ , $j+1$ 에서의 스핀 대수 표현에 대한 2차 Casimir 연산자로, 스핀 1/2 및 3/2 표현의 직접 합으로 분해할 수 있습니다.스핀 1/2 부분 공간에 대해 고유값 ${\frac {1}{2}}({\frac {1}{2}}+1)=3/4$ ( ${\frac {1}{2}}({\frac {1}{2}}+1)=3/4$ 2 + ${\frac {1}{2}}({\frac {1}{2}}+1)=3/4$ ) ${\frac {1}{2}}({\frac {1}{2}}+1)=3/4$ / ${\frac {1}{2}}({\frac {1}{2}}+1)=3/4$ ({\ $frac {1}$ ${2}}$ ({\ $frac {$ 1 $}$ + 1) = ${\frac {1}{2}}({\frac {1}{2}}+1)=3/4$ 3/ ${\frac {3}{2}}({\frac {3}{2}}+1)=15/4$ ( ${\frac {3}{2}}({\frac {3}{2}}+1)=15/4$ 2 ${\frac {3}{2}}({\frac {3}{2}}+1)=15/4$ + ${\frac {3}{2}}({\frac {3}{2}}+1)=15/4$ ) ${\frac {3}{2}}({\frac {3}{2}}+1)=15/4$ $15$ ${\frac {3}{2}}({\frac {3}{2}}+1)=15/4$ ({ $displaystyle {frac {2}}$ {\ $frac}}$ {1} = {1 $}}}}}}}$ 입니다.

접지 상태

마줌다-고시 모델은 두 개의 최소 에너지 상태, 즉 인접한 스핀 쌍이 싱글트 구성을 형성하는 상태를 가지고 있는 것으로 나타났다.각 접지 상태에 대한 파동 함수는 이러한 싱글릿 쌍의 산물입니다.이것은 하나의 격자 간격으로 시스템을 이동하거나 변환하는 것만으로 다른 시스템에서 얻을 수 있기 때문에 동일한 에너지를 가진 적어도 두 개의 접지 상태가 있어야 하는 이유를 설명합니다.또한 이들(및 이들의 선형 조합)이 고유한 접지 상태임을 보여주었다.

일반화

마줌다-고시 모델은 정확하게 풀 수 있는 소수의 사실적인 양자 스핀 모델 중 하나입니다.또한, 그 지면 상태는 원자가 결합 고체(VBS)로 알려진 단순한 예이다.따라서 마줌다-고시 모델은 또 다른 유명한 스핀 모델인 AKLT 모델과 관련이 있으며, 그 기저 상태는 독특한 1차원 스핀 1(S=1) 원자가 결합 고체이다.

마줌다르-고시 모델은 또한 무한 1차원 반홀수 스핀 시스템은 지면과 들뜬 상태 사이에 에너지 간격(또는 간격)이 없어야 하거나 둘 이상의 지면 상태를 가져야 한다는 대략적인 Lieb-Schultz-Mattis 정리의 유용한 예이다.Majumdar-Ghosh 모형은 간격이 있으며 두 번째 경우에 해당한다.

모델의 등방성은 정확히 이광화된 지면 상태를 갖는다는 사실에는 실제로 중요하지 않다. $예를 들어$ H ^ ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ j ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ ( ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ + ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ + ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ Z ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ + ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ ) ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ + ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ j ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ ( ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ X ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ + ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ + ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ + $)$ 。 $Y}_{j}{Y}_{j+1}+\delta {Z}_{j}_{j+1}+{\frac {J}{2}\sum _{j=1}^{N}({X}_{j}_{j+2}+{}{}}+{\$ $Y}_{j}{Y}_{$ j+ $2}+\delta {Z}_{j}{Z}_{$ j ${\hat {H}}=J\sum _{j=1}^{N}({X}_{j}{X}_{j+1}+{Y}_{j}{Y}_{j+1}+\delta {Z}_{j}{Z}_{j+1})+{\frac {J}{2}}\sum _{j=1}^{N}({X}_{j}{X}_{j+2}+{Y}_{j}{Y}_{j+2}+\delta {Z}_{j}{Z}_{j+2})$ +2}}}도 $\delta >-1/2$ - $\delta >-1/2$ / $\delta >-1/2$ \ $delta >-1$ /2 $\delta >-1/2$ 에 대해 전술한 것과 완전히 같은 접지 상태를 가집니다.

「」를 참조해 주세요.

레퍼런스

C K Majumdar 및 D Ghosh, 선형 체인 내 다음 인접 상호작용 시.J. 수학.물리: 10, 1388(1969); 도이 : 10.1063/1.1664978
C K Majumdar, 알려진 지면 상태의 반강자성 모델.J. 피지스C: 솔리드 스테이트 물리. 3 911 – 915 (1970)
아사 아우어바흐, 상호작용 전자와 양자 자기, 스프링거-벨라그 뉴욕 (1992) 페이지 83

^ Sushanta Kumar Dattagupta (2000). "Chanchal Kumar Majumdar (1938–2000) – An obituary". Current Science. 79 (1): 115–116.

[1] Sushanta Kumar Dattagupta (2000). "Chanchal Kumar Majumdar (1938–2000) – An obituary". Current Science. 79 (1): 115–116.

[1]

Search

마줌다-고시 모형

네임스페이스

더

목차

정의.

접지 상태

일반화

「」를 참조해 주세요.

레퍼런스

Search

마줌다-고시 모형

정의.

접지 상태

일반화

「 」를 참조해 주세요.

레퍼런스

「」를 참조해 주세요.