헤스의 법칙

헤스의 법칙으로도 알려진 헤스의 끊임없는 열분산 법칙은 1840년 이를 출판한 스위스 태생의 러시아 화학자 겸 의사 게르맹 헤스의 이름을 딴 물리화학에서의 관계다. 법은 화학 반응의 전체 과정 동안 총 엔탈피 변화는 수행된 단계의 수와 무관하다고 명시하고 있다.^[1][2]

헤스의 법칙은 이제 열역학 제1법칙에서도 표현되는 에너지 보존 원리의 표현으로 이해되고 있으며, 화학적 과정의 엔탈피가 초기부터 최종 상태까지의 경로(즉 엔탈피는 국가 기능이다)에서 독립되어 있다는 사실(즉, 엔탈피는 국가 기능이다. 반응 엔탈피 변화는 많은 반응에 대한 열량측정에 의해 결정될 수 있다. 이 값은 반응 중에 조건이 달라질 수 있지만 일반적으로 초기 및 최종 온도와 압력이 동일한 공정에 대해 명시된다. 헤스의 법칙은 화학 반응에 필요한 전체 에너지를 결정하는 데 사용될 수 있는데, 이때 화학 반응에 필요한 에너지를 개별적으로 특성화하기 쉬운 합성 단계로 나눌 수 있다. 이것은 복잡한 합성물을 설계하기 위한 기초로 사용될 수 있는 표준형성 엔탈피들의 편성을 제공한다.

이론

Hess's의 법칙은 화학 반응에서 엔탈피의 변화는 반응과 제품의 초기 상태와 최종 상태가 동일하다면, 반응이 한 단계 또는 여러 단계로 이루어지든 상관없이 동일하다고 명시하고 있다.

즉, 화학적 변화가 여러 다른 경로에 의해 일어나는 경우 화학적 변화가 발생하는 경로(초기 및 최종 조건이 동일하다고 가정할 경우)에 관계없이 전체적인 엔탈피 변화는 동일하다. 이것이 사실이 아니라면, 열역학 제1법칙을 위반할 수 있다.

헤스의 법칙은 직접 측정할 수 없는 반응에도 엔탈피 변화(ΔH)를 계산하도록 허용한다. 이는 형성의 엔탈피에 대해 이전에 결정된 값을 사용하여 반응의 화학 방정식에 기초한 기본적인 대수적 연산을 수행함으로써 이루어진다.

화학 방정식의 조합은 순 또는 전체 방정식으로 이어진다. 각 방정식에 대해 엔탈피 변화가 알려진 경우, 그 결과는 순 방정식에 대한 엔탈피 변화가 될 것이다. 순 엔탈피 변화가 음(ΔH_net < 0)이면 반응은 발열성이며 자발적일 가능성이 더 높으며, 양의 ΔH 값은 발열반응에 해당한다. 엔트로피는 또한 자발성을 결정하는데 중요한 역할을 하는데, 긍정적인 엔탈피 변화에 대한 일부 반응은 그럼에도 불구하고 자발적이기 때문이다.

헤스의 법칙에 따르면 엔탈피 변화는 부가적인 것이다. 따라서 단일 반응에 대한 ΔH

${\displaystyle \Delta H_{\text{reaction}^{\dominus }^{\delta H_{f} \\mathrm {f}^{\dominus }^{\delta H_{\mathr} \{f}}}^{\{\data}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

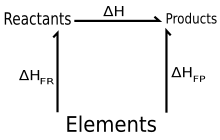
여기서 $\Delta {\displaystyle \mathrm{}}$ ${\displaystyle {}_{}}$ ${\displaystyle f_{}}$( $){\$는 제품$$ p 형성의 엔탈피, $\Delta {\displaystyle \mathrm{}}$ ${\displaystyle {}_{}}$ ${\displaystyle f_{}}$( $){\$는 반응제$$ r 형성의 엔탈피이며, 위첨자는 표준 상태 값을 나타낸다. 이는 다음과 같은 두 가지(실제 또는 가공) 반응의 합으로 간주할 수 있다.

반응제 → 원소

${\displaystyle \Delta H^{\minus }=-\\sum \Delta H_{\mathrm {f} \,({\text{r}}})^{\minus }}}}}}}}}}}$

및 요소 → 제품

${\displaystyle \Delta H^{\minus }=\sum \Delta H_{\mathrm {f} \,({\text{p}}})^{\minus }}}}}}}}}}}}$

예

1. 1. C_graphite + O₂ → CO₂ (g) ;(ΔH = -393.5 kJ/mol) (직접 단계)
   2. C_graphite + 1/2 O₂ → CO (g) ; (ΔH = −110.5 kJ/mol)
   3. CO (g) +1/2 O₂ → CO₂ (g); (ΔH = -283.02 kJ/mol)

   반응(a)은 반응(b)과 (c)의 합으로, 총 ΔH = (a)에서 ΔH와 동일한 -393.5 kJ/mol이다.

   ΔH 값 차이는 0.02 kJ/mol로 측정 오류로 인한 것이다.

2. 주어진:
   • B₂O₃ (s) + 3H₂O (g) → 3O₂ (g) + B₂H₆ (g) (ΔH = 2035 kJ/mol)
   • H₂O (l) → H₂O (g) (ΔH = 44 kJ/mol)
   • H₂ (g) + 1/2 O₂ (g) → H₂O (l) (ΔH = −286 kJ/mol)
   • 2B (s) + 3H₂ (g) → B₂H₆ (g) (ΔH = 36 kJ/mol)
   다음 ΔH를_f 구하십시오.
   • 2B (s) + 3/2 O₂ (g) → B₂O₃ (s)
   방정식(및 그 엔탈피 변화)에 적절한 요인을 곱하고 필요한 경우 방향을 반대로 적용한 후 다음과 같은 결과를 얻는다.
   • B₂H₆ (g) + 3O₂ (g) → B₂O₃ (s) + 3H₂O (g) (ΔH = 2035 × (−1) = −2035 kJ/mol)
   • 3H₂O (g) → 3H₂O (l) (ΔH = 44 × (−3) = −132 kJ/mol)
   • 3H₂O (l) → 3H₂ (g) + (3/2) O₂ (g) (ΔH = −286 × (−3) = 858 kJ/mol)
   • 2B (s) + 3H₂ (g) → B₂H₆ (g) (ΔH = 36 kJ/mol)
   이러한 방정식을 추가하고 양쪽의 공통 용어를 취소하면 우리는 얻는다.
   • 2B (s) + 3/2 O₂ (g) → B₂O₃ (s) (ΔH = −1273 kJ/mol)

자유 에너지 및 엔트로피로 확장

헤스의 법칙의 개념은 엔트로피와 깁스 자유 에너지의 변화를 포함하도록 확장될 수 있는데, 이는 국가 기능이기도 하다. 보드웰 열역학 주기는 쉽게 측정되는 평형비와 리독스 전위를 이용하여 실험적으로 접근하기 어려운 Gibbs 자유 에너지 값을 결정하는 그러한 확장의 예다. 보드웰 열역학 사이클의 ΔG^o 값과 헤스의 법칙으로 발견된 ΔH^o 값을 결합하면 직접 측정되지 않는 엔트로피 값을 결정하는 데 도움이 될 수 있으므로 대체 경로를 통해 계산해야 한다.

자유 에너지의 경우:

${\displaystyle \Delta G_{\text{reaction}^{\\minus }=\delta G_{f}\\mathrm {f}\, ({\text{p}})^{\delta G_{f}, (\text{r}}}}}}}}}}}}}).$

엔트로피로서는 상황이 좀 다르다. 엔트로피는 기준 상태(ΔH 및 ΔG와^oo 같이)에 있는 원소들의 엔트로피와 비교되지 않고 절대값으로 측정할 수 있기 때문에 형성의 엔트로피를 사용할 필요가 없다; 사람은 단지 제품과 반응제에 절대 엔트로피를 사용한다.

${\displaystyle \Delta S_{\text{reaction}^{\minus }=\sum S_{{\text{p}}}^{\sum S_{\dominus }}^{\text{r}}}}}}$

적용들

헤스의 법칙은 다음과 같은 엔탈피들의 결정에 유용하다.^[1]

1. CO와_(g) NO와_(g) 같은 불안정한 중간자 형성의 가열.
2. 위상 전환 및 편향성 전환의 열 변화.
3. 음이온을 형성하는 전자 친화력이 알려진 경우 Born-Haber를 구성하여 이온 물질의 격자 에너지
4. 이론 격자 에너지를 갖는 Born-Haber 사이클을 이용한 전자 친화력

참고 항목

• 열화학
• 열역학

참조

추가 읽기

• Leicester, Henry M. (1951). "Germain Henri Hess and the Foundations of Thermochemistry". The Journal of Chemical Education. 28 (11): 581–583. Bibcode:1951JChEd..28..581L. doi:10.1021/ed028p581.

외부 링크

• Hess's paper(1840)의 법률 근거지 (ChemTeam 사이트)
• 헤스의 법칙 실험