해먼드 추론

Hammond's postulate
George Hammond는 아이오와 주립 대학교에서 교수로 재직하는 동안 그 자리를 개발했다.

Hammond의 가정(또는 대안적으로 Hammond-Leffler 가정)은 물리적 유기 화학에 있어서의 가설이다. 이 가설은 유기 화학 반응으로 전환 상태의 기하학적 구조를 설명한다.[1] 1955년 조지 해먼드에 의해 처음 제안된 가정은 다음과 같다.[2]

예를 들어, 전환 상태와 불안정한 중간 상태와 같은 두 상태가 반응 프로세스 중에 연속적으로 발생하고 에너지 함량이 거의 동일하다면, 이들의 상호 변환은 분자 구조의 작은 재구성만 수반할 것이다.

따라서 국가의 기하학적 구조는 그 에너지를 반작용 좌표를 따라 그 주변의 종과 비교함으로써 예측할 수 있다. 예를 들어, 발열 반응에서 전환 상태는 제품보다 반응 물질에 더 가까운 에너지다. 따라서 전환 상태는 제품보다 반응 물질과 기하학적으로 더 유사할 것이다. 그러나 대조적으로 내열반응에서 전환 상태는 반응제보다 제품에 더 가까운 에너지다. 그래서, Hammond의 추정에 따르면, 전환 상태의 구조가 반응제보다 제품과 더 비슷할 것이라고 한다.[3] 대부분의 전환 상태를 실험적으로 특성화할 수 없기 때문에 이러한 유형의 비교는 특히 유용하다.[4]

해먼드의 추론은 벨-에반스-폴라니 원리를 설명하고 합리화하는 데도 도움이 된다. 즉, 이 원리는 반응 속도, 즉 반응의 활성화 에너지가 그 반응의 엔탈피에 의해 영향을 받는다는 실험적인 관찰을 설명한다. Hammond의 가정은 반응의 엔탈피가 얼마나 변화하여 전환 상태의 구조도 변화시킬 것인가를 설명함으로써 이러한 관찰을 설명한다. 결국, 기하학적 구조의 이러한 변화는 전환 상태의 에너지를 변화시킬 것이고, 따라서 활성화 에너지와 반응 속도도 변화시킬 것이다.[5]

가설은 반응 좌표도의 모양을 예측하는 데도 사용되었다. 예를 들어, 전기영양 방향족 치환에는 구별되는 중간 상태와 잘 정의되지 않은 두 개의 상태가 포함된다. 방향족 대체물의 효과를 측정하고 해몬드의 추정을 적용함으로써 요율 결정 단계는 중간 복합체를 닮아야 하는 전환 상태 형성을 수반한다는 결론을 내렸다.[6]

역사

1940년대와 1950년대에 화학자들은 반응 물질의 작은 변화조차도 반응의 속도와 제품 분포에 상당한 차이를 야기하는 이유를 설명하는데 어려움을 겪었다. 1955년 아이오와 주립대학의 젊은 교수인 조지 해먼드는 전환국가 이론이 관측된 구조-반응성 관계를 질적으로 설명하는데 사용될 수 있다고 가정했다.[7] 특히, 플로리다 주립 대학의 존 E. 레플러는 1953년에 비슷한 생각을 제안했다.[8] 그러나 해먼드 버전은 질적인 성질이 레플러의 복잡한 수학 방정식보다 이해하기 쉽고 채용하기 쉬웠기 때문에 더 많은 관심을 받았다. 해몬드의 추측은 때때로 두 과학자에게 공로를 돌리는 하몬드-레플러 추론이라고 불린다.[7]

가정 해석

효과적으로, 이 가정은 전환 상태의 구조가 자유 에너지에서 가장 가까운 종의 구조와 유사하다고 말한다. 이는 잠재적 에너지 다이어그램을 참조하여 설명할 수 있다.

Energy diagrams showing how to interpret Hammond's Postulate

발열 반응인 (a)의 경우, 전환 상태의 에너지는 중간이나 제품의 에너지보다 반응물질의 에너지에 더 가깝다. 따라서, 가정으로부터, 전이 상태의 구조도 반응제의 구조와 더 밀접하게 유사하다. 만일 (b)의 경우, 전환 상태의 에너지가 반응제나 생산물에 가깝지 않아 전환 상태의 좋은 구조적 모델이 되지 못한다. 전환 상태의 구조나 특성을 예측하기 위해서는 추가 정보가 필요할 것이다. 사례(c)는 내열반응에 대한 잠재적 도표를 나타내며, 가정집행에 따라 전환 상태가 중간 또는 제품의 그것과 더 밀접하게 유사해야 한다.

해몬드가 추정한 또 다른 의의는 우리가 반응제, 매개체, 또는 제품 측면에서 전환 상태의 구조를 논의할 수 있게 해준다는 것이다. 전환 상태가 반응제와 매우 유사한 경우, 전환 상태를 "조기"라고 하며, "후기" 전환 상태는 중간 또는 제품과 매우 유사한 상태를 말한다.[9]

"초기" 전이 상태의 예는 염소 처리다. 염소화 작용은 발열반응이기 때문에 제품을 선호하는데, 이는 제품이 반응 물질보다 에너지가 낮다는 것을 의미한다.[10] 인접한 도표("초기" 전환 상태를 나타냄)를 볼 때, 실험 중에 관찰할 수 없는 전환 상태에 초점을 맞추어야 한다. "조기" 전환 상태가 의미하는 바를 이해하기 위해, Hammond postulate는 이 반응의 운동학을 보여주는 곡선을 나타낸다. 반응 물질은 에너지가 더 높기 때문에, 전환 상태는 반응이 시작된 직후에 나타나는 것으로 보인다.

"후기" 전환 상태의 예는 브롬화다. 브롬화는 내열반응이기 때문에 반응제를 선호하는데, 이는 반응제가 제품보다 에너지가 낮다는 것을 의미한다.[11] 전환 상태를 관찰하기 어렵기 때문에 브롬화의 가정은 "후기" 전환 상태를 그려내는 데 도움이 된다("후기" 전환 상태의 표현 참조). 제품들은 에너지가 더 높기 때문에, 전환 상태는 반응이 완성되기 바로 직전인 것처럼 보인다.

유기화학 교과서에서 흔히 발견되는 가설의 다른 유용한 해석은 다음과 같다.

불안정한 중간체와의 반응에 대한 전이 상태는 중간체 자체에 의해 근접하게 추정될 수 있다고 가정한다.[필요하다]

이 해석은 상대적으로 특이하고 보통 가장 불안정한 중간체와의 과도상태와 관련된 극도로 발열성 및 내열반응을 무시한다.

전환 상태 구조

S1N 반응

S1N 반응의 에너지 다이어그램

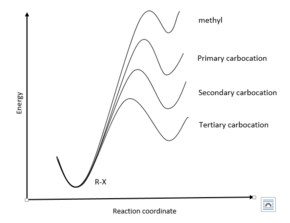
Hammond의 가정은 SN1 반응의 전환 상태 구조를 검사하는 데 사용될 수 있다. 특히 탈퇴군의 분열은 S1반응의N 첫 번째 전환상태다. 이 분화에 의해 형성된 탄화물의 안정성은 트렌드 3차 > 2차 > 1차 > 메틸을 따르는 것으로 알려져 있다.

따라서 3차 탄수화물은 비교적 안정적이고 따라서 R-X 반응물질에 에너지가 가깝기 때문에 3차 전환 상태는 R-X 반응물질과 상당히 유사한 구조를 가질 것이다. 반응 좌표 대 에너지의 그래프로 볼 때, 이것은 3차 전환 상태가 다른 전환 상태보다 더 왼쪽에 있다는 사실에 의해 보여진다. 이와는 대조적으로 메틸 탄수화물의 에너지는 매우 높으며 따라서 전환 상태의 구조는 R-X 반응제보다 중간 탄수화물과 더 유사하다. 이에 따라 메틸 전이 상태는 오른쪽이 매우 멀다.

S2N 반응

양분자 핵 대체(SN2) 반응은 핵소체와 기질이 모두 속도 제한 단계에 관여하는 결합 반응이다. 이 반응이 일치하기 때문에 한 번에 반응이 일어나는데, 여기서 채권이 깨지고 새로운 채권이 형성된다.[12] 따라서 이러한 반응을 해석하기 위해서는 합치된 요율 제한 단계를 닮은 전환 상태를 살펴보는 것이 중요하다. "S2N 반응의 저하" 그림에서, 핵소체는 탄소에 새로운 결합을 형성하는 반면, 할리드(L) 결합은 깨진다.[13]

E1 반응

단분자 제거 반응 메커니즘

E1 반응은 단분자 제거로 구성되며, 여기서 메커니즘의 속도 결정 단계는 단일 분자 종의 제거에 의존한다. 이것은 2단계 메커니즘이다. 탄수화물 중간이 안정적일수록 반응이 빨라져 제품에 유리하다. 탄수화물 중간을 안정화시키면 활성화에너지가 낮아진다. 반응도 순서는 (CH3)3C- > (CH3)2CH- > CH3CH2- > CH3-이다.[14]

단분자 제거 반응 좌표

게다가, 연구는 정력적으로 동등한 두 개의 항산화제로 시작하여 결국 두 개의 에너지-인분산 매개체를 형성하는 전형적인 운동 분해능 과정을 설명한다. 해몬드의 추정에 따르면, 안정성이 높은 이질성분열체가 더 빨리 형성된다.[15]

E2 반응

제거, 양분자 반응은 기본과 기질이 모두 속도 제한 단계에 참여하는 결합 반응이다. E2 메커니즘에서, 기지는 떠나는 그룹 가까이에 양성자를 가져가고, 전자는 이중 결합을 하도록 강요하고, 떠나는 그룹 모두를 하나의 일치된 단계로 강제한다. 요율법은 반응제 2개의 1차 농도에 따라 달라져 2차(분자) 제거반응이 된다. 속도 결정 단계에 영향을 미치는 요인은 입체화학, 이탈군, 기저강도 등이다.

E2 반응에 대해 Joseph Bunnett의 이론에 따르면, 반응물과 제품 사이의 에너지 장벽을 통과하는 가장 낮은 통과는 전환 상태에서β C-H와α C-X 파열 정도 사이의 조절에 의해 얻어진다고 한다. 그 조정은 훨씬 더 쉽게 끊어질 수 있고, 적은 양의 끊어질 수 있는 에너지를 필요로 하는 결합을 포함한다.[16] Bunnett에 의한 이러한 결론은 Hammond의 가정으로부터의 모순이다. Hammond postulate는 Bunnett이 이론화한 것과는 정반대다. 채권단절단계의 전환상태에서 그것은 그 결합이 쉽게 깨질 때 거의 깨지지 않고 깨지기 어려울 때 많이 깨지는 것을 포함한다.[16] 이러한 차이에도 불구하고, 두 집정관은 서로 다른 종류의 과정에 관심을 가지고 있기 때문에 충돌하지 않는다. 해먼드는 한 개의 결합이 만들어지거나 깨지거나, 두 개 이상의 결합이 시간 끌지 않고 동시에 이뤄지는 반응 단계에 초점을 맞춘다. E2 이론 전환 상태는 결합 형성과 파괴가 동시에 이루어지지 않을 때의 과정에 관한 것이다.[16]

키네틱스와 벨-에반스-폴라니 원리

기술적으로 해먼드의 가정은 화학반응의 기하학적 구조만을 기술한다. 그러나 해먼드의 가정은 반응의 속도, 운동학, 활성화 에너지에 대한 정보를 간접적으로 제공한다. 따라서 유사한 반응의 엔탈피와 비율이 대개 상관관계가 있었다는 실험 관측을 기술하는 벨-에반스-폴라니 원리를 이해할 수 있는 이론적 근거를 제공한다.

S1N 반응의 에너지 다이어그램

Hammond의 가정과 BEP 원리의 관계는N S1 반응을 고려함으로써 이해할 수 있다. S1N 반응(떠나는 집단의 분열 후 핵에 의한 공격) 중에 두 가지 전환 상태가 발생하지만, 떠나는 집단의 분열은 거의 항상 요율을 결정하는 단계다. 따라서 활성화 에너지와 반응 속도는 오직 분리 단계에 따라 달라질 것이다.

첫째, 2차 탄소와 3차 탄소의 반응을 고려한다. BEP 원리에 따르면, 3차 탄소의 S1N 반응은 2차 탄소의 경우보다 실험적으로 더 빠르다. 따라서 정의상 3차 반응의 전환 상태는 2차 반응보다 낮은 에너지에 있을 것이다. 그러나 BEP 원칙은 왜 에너지가 더 낮은지를 정당화할 수 없다.

해몬드의 추정을 사용하면 3차 전환 상태의 낮은 에너지는 그 구조가 2차 케이스에 비해 탄수화물 제품보다 반응제 R(3차)-X에 상대적으로 더 가깝다는 것을 의미한다. 따라서 3차 전환 상태는 2차 전환 상태가 R(2차)-X 반응제와 기하학적으로 더 유사할 것이다. 따라서 3차 전환 상태가 (낮은 에너지) 반응제에 구조적으로 가깝다면, 구조가 에너지를 결정하기 때문에 에너지에서도 낮아질 것이다. 마찬가지로 2차 전환 상태가 (고에너지) 탄수화물 제품과 더 유사하다면, 에너지에서 더 높을 것이다.

가정 적용

해몬드의 가정은 반응 속도와 제품의 안정성 사이의 관계를 이해하는 데 유용하다. 반응 속도는 활성화 에너지에만 의존하지만(흔히 유기 화학에서‡ ΔG "delta G 이중 단도"로 표현되는 반면, 화학 평형에서 제품의 최종 비율은 표준 자유 에너지 변화 ΔG("delta G")에만 의존한다. 평형상태에서 최종제품의 비율은 그러한 제품의 안정성과 직접적으로 일치한다.

Hammond의 가정은 에너지에서 매우 가까운 두 상태를 포함하는 단계에서는 분자 재구성이 작아야 한다고 말함으로써, 반응 과정의 속도를 그것의 일부를 이루는 상태의 구조적 특징과 연결시킨다. 이것은 시작 재료와 제품, 그리고 가능한 "안정적인 매개체" 사이의 구조적 비교를 낳았고, 이로 인해 가장 안정적인 제품이 항상 반응 과정에서 선호되는 것은 아니라는 것을 이해하게 되었다.

겉보기에 모순되는 결과를 설명함

해몬드의 가정은 반응의 속도 제한 단계를 볼 때 특히 중요하다. 단, 다단계 반응을 검사할 때 또는 중간 단계에서 재배열 가능성이 있는 반응을 검사할 때는 주의해야 한다. 경우에 따라서는 최종 제품이 보다 안정적인 제품(열역학 제품)보다는 불안정한 제품(키네틱 제품이라고 함)에 유리하게 치우친 비율로 나타나는 경우도 있다. 이 경우 요율 제한 단계와 중간자를 검토해야 한다. 종종 속도 제한 단계는 탄수화물 같은 불안정한 종의 초기 형성이다. 그런 다음 탄수화물이 형성되면 후속 재배치가 발생할 수 있다. 이러한 종류의 반응에서, 특히 낮은 온도에서 실행될 때, 반응 물질은 더 안정적인 중간을 형성하는 데 필요한 재배열 전에 반응한다. 미세한 반전이 쉬운 고온에서는 이들 중간체가 재배열할 시간이 있기 때문에 보다 안정적인 열역학 제품을 선호한다. 고온에서 달리든 저온에서 달리든 운동학적 제품과 열역학적 제품의 혼합은 미세역반으로 인해 평준화 시간이 주어지면 결국 보다 안정적인 열역학적 제품에 유리한 동일한 비율에 도달하게 된다.

참고 항목

참조

  1. ^ Fox MA, Whiteshell JK (2004). Organic Chemistry. Sudbury, Massachusetts: Jones and Bartlett Publisher s. pp. 355–357. ISBN 978-0-7637-2197-8.
  2. ^ Hammond, G. S. (1955). "A Correlation of Reaction Rates". J. Am. Chem. Soc. 77 (2): 334–338. doi:10.1021/ja01607a027.
    솔로몬스, T.W. 그래함 & 프라이얼, 크레이그 B. (2004) 유기화학(8부) 존 와일리 & 선즈 주식회사 ISBN0-471-41799-8.
    Loudon, G. Marc. "유기 화학" 2005년 4월 4일.
  3. ^ Carey FA, Sundberg R (2007). Advanced Organic Chemistry Part A:Structure and Mechanisms. Norwell: Springer.
  4. ^ Anslyn EV, Dougherty DA (2006). Modern Physical Organic Chemistry. Sausalito, CA: University Science.
  5. ^ McMurry J (1992). Organic Chemistry. Pacific Grove, CA: Brooks/Cole. pp. 246–248.
  6. ^ Carey FA, Sundberg RJ (1990). Advanced Organic Chemistry.-Part A: Structure and Mechanism. New York, NY: Plenum.
  7. ^ a b Yarnell A (2003). "Hammond Postulate: 1955 paper used transition-state theory to explain structure-reactivity relationships". Chemical & Engineering News. 81 (20): 42. doi:10.1021/cen-v081n020.p042.
  8. ^ Leffler JE (March 1953). "Parameters for the Description of Transition States". Science. 117 (3039): 340–1. Bibcode:1953Sci...117..340L. doi:10.1126/science.117.3039.340. PMID 17741025.
  9. ^ Meany JE (1 February 2001). "Application of Hammond's postulate". Journal of Chemical Education. 01. 2 (78): 204. Bibcode:2001JChEd..78..204M. doi:10.1021/ed078p204.
  10. ^ Fox MA, Whitesell JK (2004). Organic Chemistry Third Edition. Sudbury, MA: Jones and Barlett Publishers. p. 356.
  11. ^ Sorrell TN (2005). Organic Chemistry Third Edition. Sausalito, CA: University Science Books. pp. 370–371.
  12. ^ Anslyn EV, Brown WH, Foote CS, Iverson BL (2009). Organic Chemistry Fifth Edition. Belmont, CA: Brooks/Cole Cengage Learning. p. 333.
  13. ^ Curtis R (October 2, 2013). "Kinetics of Nucleophilic Substitution Reactions". Chemwiki. UCDavis. Retrieved November 21, 2015.
  14. ^ Justik MW. "Review of SN1, SN2, E1, and E2" (PDF).
  15. ^ Rajendran KV, Nikitin KV, Gilheany DG (July 2015). "Hammond Postulate Mirroring Enables Enantiomeric Enrichment of Phosphorus Compounds via Two Thermodynamically Interconnected Sequential Stereoselective Processes". Journal of the American Chemical Society. 137 (29): 9375–81. doi:10.1021/jacs.5b04415. PMID 26186272.
  16. ^ a b c Bunnett J (1962). Survey of Progress in Chemistry. New York: Academic. pp. 70–72.

추가 읽기