그래프 재작성

컴퓨터 과학에서 그래프 변환 또는 그래프 재작성은 알고리즘으로 원본 그래프에서 새로운 그래프를 만드는 기술과 관련이 있습니다.소프트웨어 엔지니어링(소프트웨어 구축 및 소프트웨어 검증)부터 레이아웃 알고리즘 및 이미지 생성까지 다양한 애플리케이션을 제공합니다.

그래프 변환을 계산 추상화로 사용할 수 있습니다.기본적인 생각은 계산의 상태를 그래프로 나타낼 수 있는 경우, 그 계산의 추가 단계를 그래프에 변환 규칙으로 나타낼 수 있다는 것입니다.이러한 규칙은 완전한 상태의 하위 그래프와 일치해야 하는 원본 그래프와 일치된 하위 그래프를 대체하는 대체 그래프로 구성됩니다.

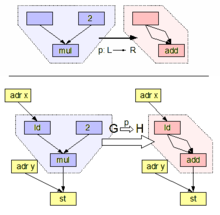
일반적으로 그래프 개서 시스템은 L ${\displaystyle \to }$ ${\displaystyle R}${\$displaystyle$L\$right$ 화살표 R$\}$ $형식$의 그래프 개서 규칙 세트로 $구성$됩니다. L ${\displaystyle$ L$}$은 패턴 그래프(또는 왼쪽)라고 하며$$R {\$displaystyle$ R$}$은 대체 그래프(또는 규칙의 오른쪽)라고 합니다.호스트 그래프에는 패턴 그래프의 발생을 탐색하고(패턴 매칭으로 서브그래프 동형성 문제를 해결), 검출된 발생을 치환 그래프의 인스턴스로 치환함으로써 그래프 개서 규칙을 적용한다.개서 규칙은 문자열 규제 그래프 문법 등 라벨이 부착된 그래프의 경우 더욱 규제할 수 있습니다.

때때로 그래프 문법은 그래프 재작성 시스템의 동의어로 사용됩니다. 특히 형식 언어의 맥락에서; 다른 표현은 단순히 주어진 상태(호스트 그래프)를 변환하는 대신 어떤 시작 그래프에서 모든 그래프의 열거와 같은 구성 목표를 강조하기 위해 사용됩니다.새로운 상태로.

그래프 재작성 방법

대수적 접근

그래프 재작성에 대한 대수적 접근은 범주 이론에 기초한다.대수적 접근법은 하위 접근법으로 더 세분화되며, 가장 일반적인 접근법은 이중 푸시아웃(DPO) 접근법과 단일 푸시아웃(SPO) 접근법이다.기타 서브접근법에는 sesqui-pushout 및 풀백접근법이 있습니다.

DPO 접근법의 관점에서 그래프 재작성 규칙은 그래프 범주 내 형태소 쌍으로, ${\displaystyle r}$ ${\displaystyle =}$ ( L ${\displaystyle \leftarrow }$ ${\displaystyle K}$ ${\displaystyle \to R}$) ( \ $displaystyle r =$( L \ $left 화살표$K \ $rightarrow$ R$$)$$, $L{\displaystyle }$ ${\displaystyle \supseteq }$ ${\displaystyle K}$ $display style LSU$ \ substyle$LSU$ .주입식그래프 K를 불변 그래프 또는 접착 그래프라고 합니다.호스트 그래프 G에 대한 규칙 r의 개서 단계 또는 적용은 모두 동일한 ${\displaystyle \mathrm{형태론}}$k: K $→$ ${\displaystyle D}$ \ $display$k \ $display$ K \ $right row$ D$$（ D ） 。여기서 D는 콘텍스트 그래프(이러한 이름의 이중화살표)에서 유래한다.${\displaystyle 또}$ 다른 그래프 $형태론{\displaystyle }$m : L ${\displaystyle \to }$ {\$displaystyle$ m$\rightarrow$ G$}$는 G에서 L의 발생을 모형화하여 일치라고 한다.L {\$displaystyle$ L$}$은 G$${\$displaystyle$ G$}$와 일치하는 서브그래프이며(서브그래프 동형 문제 참조), 일치한 후 $호스트{\displaystyle }$ 그래프$G$ {\$displaystyle$G$}$에서$$L {\$displaystyle$ L$}$은 R$${\$displaystyle$ R$}$로 $대체$됩니다$.$는 인터페이스로서 규칙 적용 시 유지되는 노드 및 엣지를 포함합니다.$그래프{\displaystyle }$ K(\$displaystyle$ K$)$는 일치하는 패턴을 컨텍스트에 첨부하기 위해 필요합니다.이 패턴이 비어 있는 경우 그래프 $(\displaystyle$ G$)$의 연결된 컴포넌트 전체를 지정할 수 있습니다.

반면 SPO 접근법의 그래프 개서 규칙은 ${\displaystyle \mathrm{라벨}}$이 부착된 멀티그래프 및 부분 매핑 카테고리의 단일 모르피즘으로 멀티그래프 $구조$를 ${\displaystyle \mathrm{보존}}$한다$:$ r : L ${\displaystyle \to }$ R \ $displaystyle$r \ $rightarrow$ R$\}$ 。따라서 개서 단계는 단일 푸시아웃 다이어그램으로 정의된다.이에 대한 실질적인 이해는 DPO 접근법과 유사합니다.차이점은 호스트 그래프 G와 개서 스텝의 결과인 그래프 G' 사이에 인터페이스가 없다는 것이다.

실용적인 관점에서 DPO와 SPO의 주요 차이점은 인접한 에지를 가진 노드의 삭제, 특히 그러한 삭제가 "덩글링 에지"를 남기지 않도록 하는 방법입니다.DPO 접근법은 규칙이 인접 에지도 모두 삭제하도록 지정되어 있는 경우(이러한 행잉 조건은 특정 일치에 대해 확인할 수 있음) 노드만 삭제하는 반면 SPO 접근법은 명시적인 사양 없이 인접 에지를 단순히 폐기합니다.

그래프 개서에 대한 또 다른 대수적 접근법도 있는데, 주로 부울 대수와 행렬 대수에 기초하며, 매트릭스 그래프 ^[1]문법이라고 불립니다.

그래프 재작성 결정

그러나 결정 그래프 재작성이라고 알려진 그래프 재작성에 대한 또 다른 접근법은 논리와 데이터베이스 ^[2]이론에서 나왔다.이 접근법에서는 그래프는 데이터베이스 인스턴스로 취급되어 쿼리 및 뷰를 정의하기 위한 메커니즘으로서 개서 조작이 이루어집니다.따라서 모든 개서 조작은 고유한 결과(이형성까지)를 생성하기 위해 필요합니다.이는 그래프 전체에 적용되는 모든 개서 규칙을 동시에 적용함으로써 실현됩니다.이러한 변경 조작은, 예를 들면, 어느 장소에 관계없이, 그 그래프 전체에 걸쳐 행해집니다.ult는 실제로 고유하게 정의되어 있습니다.

용어 그래프 다시 쓰기

그래프 개서를 위한 또 다른 접근법은 용어 그래프 개서입니다.이것은 구문 개서 규칙에 의한 용어 그래프(추상 의미 그래프라고도 함)의 처리 또는 변환을 수반합니다.

용어 그래프 재작성 규칙은 컴파일러의 운영 의미를 공식적으로 표현할 수 있기 때문에 용어 그래프는 프로그래밍 언어 연구에서 중요한 주제이다.용어 그래프는 동시성 모델과 같은 그래픽 계산뿐만 아니라 화학 및 생물학적 계산을 모델링할 수 있는 추상 기계로도 사용된다.용어 그래프는 1차 논리에서의 수량화된 스테이트먼트의 표현에 적합하기 때문에 자동 검증과 논리 프로그래밍을 실행할 수 있습니다.기호 프로그래밍 소프트웨어는 그룹, 필드 및 링과 같은 추상 대수 구조를 표현하고 계산을 수행할 수 있는 용어 그래프를 위한 또 다른 응용 프로그램입니다.

TERMGRAPH 컨퍼런스는^[3] 용어 그래프 재작성과 그 응용에 대한 연구에 전적으로 초점을 맞추고 있습니다.

그래프 문법 및 그래프 개서 시스템 클래스

그래프 개서 시스템은 사용되는 그래프의 종류와 개서가 표현되는 방법에 따라 자연스럽게 클래스로 그룹화됩니다.그래프 문법이라는 용어는 그래프 재작성 시스템 또는 그래프 대체 시스템과 동등하며 분류에서 가장 자주 사용됩니다.일반적인 유형은 다음과 같습니다.

• 그래프 재작성에 대한 대수적 접근법에 대해 위 절에서 언급한 대체 특성화를 위한 단일 푸시아웃 접근법 또는 이중 푸시아웃 접근법 중 하나를 사용하여 일반적으로 공식화된 속성 그래프 문법.
• 보다 제한적인 하위 클래스인 포트 그래프 문법, 선형 그래프 문법 및 상호 작용 망을 포함한 하이퍼 그래프 문법.

구현 및 응용 프로그램

그래프는 관계에 의해 연결된 객체(엔티티)의 모델링을 위한 표현적, 시각적, 수학적으로 정확한 형식주의이다. 객체는 노드로 표현되고 이들 사이의 관계는 모서리로 표현된다.노드 및 가장자리는 일반적으로 유형화되고 속성이 지정됩니다.이 모델에서 계산은 개체 간의 관계 변경 또는 그래프 요소의 속성 변경으로 설명됩니다.그래프 개서/그래프 변환 규칙으로 인코딩되며 그래프 개서 시스템/그래프 변환 도구로 실행됩니다.

• 응용 프로그램 도메인 중립 도구:
  • AGG, 속성 그래프 문법 시스템(Java)
  • GP 2는 그래프 변환 규칙의 직접적인 적용에 의한 그래프 컴퓨팅을 위한 프로그래밍 언어입니다.
  • 그래프 매칭 및 변환을 위한 그래프 매칭 및 변환 엔진인 GMTE.C++를 사용한 Messmer 알고리즘의 확장 구현입니다.
  • GrGen.NET, 그래프 개서 생성기, C#-code 또는 를 출력하는 그래프 변환 도구.NET 어셈블리
  • 그래프 및 그래프 변환 규칙을 편집하고 그래프 문법의 상태 공간을 탐색하며 이러한 상태 공간을 확인하는 Java 기반 도구 세트인 GROVE는 그래프 변환 엔진으로도 사용할 수 있습니다.
  • Verigraph는 그래프 개서(Haskell)에 기반한 소프트웨어 사양 및 검증 시스템입니다.
• 그래프 개서를 통해 소프트웨어 엔지니어링 태스크(주로 MDA)를 해결하는 도구:
  • 스토리 기반 모델링 및 트리플 그래프 그래머를 지원하는 EMF 호환 모델 변환 도구인 eMoflon
  • EMF를 기반으로 한 그래프 재작성 시스템을 EMorF하여 인플레이스 및 모델 간 변환을 지원합니다.
  • Fujaba는 PROGRES에 기반한 그래프 개서 언어인 Story Driven Modeling을 사용합니다.
  • 그래프 데이터베이스는 종종 그래프의 동적 재작성을 지원합니다.
  • 엄청나
  • 그래프 기반 프로그래밍 언어인 Gremlin(그래프 다시 쓰기 참조)
  • EMF를 기반으로 한 그래프 재작성 시스템인 Hensin은 인플레이스 및 모델 간 변환, 임계 쌍 분석 및 모델 확인을 지원합니다.
  • PROGRES: PRO 프로그램된 그래프 리라이트 시스템용 통합 환경 및 고급 언어
  • 비아트라
• 기계 공학 공구
  • GraphSynth는 제한 없는 그래프 문법을 만들고 결과 언어 변형을 테스트 및 검색하기 위한 인터프리터 및 UI 환경입니다.그래프와 그래프 문법 규칙을 XML 파일로 저장하고 C#에 씁니다.
  • Soley Studio는 그래프 변환 시스템을 위한 통합 개발 환경입니다.주요 응용 분야는 엔지니어링 분야의 데이터 분석입니다.
• 생물학 응용 프로그램
  • 그래프 문법 기반 언어를 사용한 기능-구조 플랜트 모델링
  • 문자열 규제 그래프 문법을 사용한 다세포 개발 모델링
• 인공지능/자연어 처리
  • OpenCog는 다양한 AI 알고리즘을 구현하기 위해 사용되는 기본 패턴 매처(하이퍼그래프)를 제공합니다.
  • RelEx는 그래프 개서를 사용하여 링크 해석을 의존성 해석으로 변환하는 영어 파서입니다.
• 컴퓨터 프로그래밍 언어
  • Clean 프로그래밍 언어는 그래프 개서를 사용하여 구현됩니다.

「 」를 참조해 주세요.

• 그래프 이론
• 도형 문법
• 형식 문법
• 추상 개서 - 그래프 개서의 일반화

레퍼런스

인용문

원천