거대 자기 저항

거대자기저항(GMR)은 강자성층과 비자성 도전층으로 이루어진 다층층에서 관찰되는 양자역학적 자기저항 효과입니다.2007년 노벨 물리학상은 GMR의 발견으로 Albert Pert와 Peter Grünberg에게 수여되었다.

이 효과는 인접한 강자성층의 자화가 평행인지 역평행인지에 따라 전기 저항이 크게 변화한 것으로 관찰됩니다.전체 저항은 병렬 정렬의 경우 상대적으로 낮고 역평행 정렬의 경우 상대적으로 높습니다.예를 들어 외부 자기장을 적용하여 자화 방향을 제어할 수 있습니다.그 효과는 스핀 방향에 대한 전자 산란의 의존성에 기초한다.

GMR의 주요 응용 분야는 하드 디스크 드라이브, 바이오 센서, 마이크로 전기 전자 시스템(MEMS) 및 기타 ^[1]장치의 데이터를 읽는 데 사용되는 자기장 센서입니다.GMR 멀티레이어 구조는 자기저항 랜덤액세스 메모리(MRAM)에서도 1비트의 정보를 저장하는 셀로서 사용됩니다.

문헌에서 거대 자기 저항이라는 용어는 다층 ^[2][3]구조와 관련이 없는 강자성 및 반강자성 반도체의 거대한 자기 저항과 혼동되기도 한다.

공식화

자기 저항은 외부 자기장의 강도에 대한 샘플의 전기 저항의 의존성입니다.수치상으로는 다음과 같은 값이 특징입니다.

${\displaystyle _{H}=sq frac {R(H)-R(0)}{R(0)}}$

여기서 R(H)는 자기장 H에서 샘플의 저항이고, R(0)은 H =^[4] 0에 해당한다. 이 식의 대체 형태는 저항 대신 전기 저항률,^[5] θ에_H 대한 다른 부호를 사용할 수 있으며, 때로는 R(0)^[6]가 아닌 R(H)로 정규화되기도 한다.

"거대자기저항"이라는 용어는 다층 구조의 값 θ가_H 일반적인 ^[7][8]값이 수 퍼센트 이내인 이방성 자기저항을 크게 초과함을 나타냅니다.

역사

GMR은 1988년^[9][10] 프랑스 파리수드 대학의 알베르 페르와 독일 포르스첸트룸 율리히의 페터 그룬베르크 그룹에 의해 독립적으로 발견되었다.이 실험적인 발견의 ^[11]실질적인 의미는 2007년 페르트와 그룬베르크에게 수여된 노벨 물리학상에 의해 인정되었다.

초기 단계

고체 내 전하 운반체의 이동성에 대한 자화의 영향을 설명하는 첫 번째 수학적 모델은 1936년에 보고되었다.§의_H 잠재적 강화에 대한 실험적 증거는 1960년대부터 알려져 왔다.1980년대 후반까지 이방성 자기저항은 잘 ^[12][13]연구되었지만, 그에 상응하는 δ의_H 값은 몇 ^[7]퍼센트를 넘지 않았다.δ의_H 강화는 수 나노미터 ^[14]두께의 다층 박막을 제조할 수 있는 분자 빔 에피택시 등의 샘플 준비 기술의 등장으로 가능해졌다.

실험과 그 해석

Pert와 Grünberg는 강자성 물질과 비강자성 물질을 포함하는 구조의 전기 저항을 연구했습니다.특히 Pert는 다층 필름에 대해 연구했고 1986년 Grünberg는 Fe/Cr ^[14]필름에서 반강자성 교환 상호작용을 발견했다.

GMR 발견 작업은 두 그룹이 약간 다른 샘플에 대해 수행했습니다.Pert 그룹은 (001)Fe/(001) Cr 초격자를 사용했는데, 이때 Fe 및 Cr층은 20°C로 유지된 (001) GaAs 기판에 고진공 상태로 퇴적되고 자기저항 측정은 저온(일반적으로 4.2K)^[10]에서 수행되었습니다.Grünberg 작업은 ^[9]실온에서 (110) GaAs의 Fe와 Cr의 다층에 대해 수행되었습니다.

3nm 두께의 철층을 가진 Fe/Cr 다층에서는 비자성 Cr층의 두께를 0.9nm에서 3nm로 늘리면 Fe층 간의 반강자성 결합이 약해지고 탈자장이 감소하여 시료를 4.2K에서 실온으로 가열했을 때도 감소하였다.비자성층의 두께를 변경하면 이력 루프의 잔류 자화가 현저하게 감소했습니다.외부 자기장이 4.2K일 때 전기 저항이 최대 50% 변화했습니다.퍼트는 이방성 자기 ^[10][15]저항과의 차이를 강조하기 위해 이 새로운 효과를 거대 자기 저항이라고 명명했다.그룬베르크 실험에서도^[9] 같은 사실을 발견했지만, 샘플이 저온이 아닌 실온에 있었기 때문에 (50%에 비해) 효과가 덜 뚜렷했다.

발견자들은 그 효과가 초격자에서 전자의 스핀 의존 산란, 특히 자화와 전자 ^[9][10]스핀의 상대적 방향에 대한 층의 저항 의존성에 기초한다고 제안했다.전류의 다른 방향에 대한 GMR 이론은 다음 몇 년 동안 개발되었습니다.1989년 Camley와 Barna calcul는 고전적 ^[16]근사치로 전류가 층을 따라 흐르는 "평면 전류"(CIP) 기하학을 계산했다.양자 형식주의를 ^[17]사용했어요층에 수직인 전류에 대한 GMR 이론(평면에 수직인 전류 또는 CPP 기하학)은 1993년에 ^[18]보고되었습니다.CPP^[19] 지오메트리는 자기저항비(θ_H)^[20]가 커지기 때문에 디바이스 ^[21]감도가 높아지기 때문에 어플리케이션은 CPP 지오메트리를 선호합니다.

이론.

기초

스핀 의존 산란

자기순서 재료에서 전기저항은 결정학적으로 동등한 원자가 0이 아닌 자기모멘트를 가진 결정체상의 자기아격자상의 전자의 산란에 의해 결정적으로 영향을 받는다.산란은 전자 스핀과 그 자기 모멘트의 상대적인 방향에 따라 달라집니다: 그것은 평행할 때 가장 약하고 반평행일 때 가장 강합니다; 그것은 원자의 자기 모멘트가 무작위 ^[7][22]방향을 갖는 상사성 상태에서 상대적으로 강합니다.

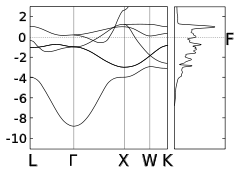
금이나 구리와 같은 양호한 도체의 경우 페르미 레벨이 sp 밴드 내에 있고 d밴드가 완전히 채워져 있습니다.강자석에서 전자-원자 산란의 자기 모멘트 방향에 대한 의존성은 철, 니켈 또는 코발트에 대한 3d 밴드 등 금속의 자기 특성을 담당하는 밴드의 충전과 관련이 있다.강자석의 d밴드는 위아래로 회전하는 전자의 수가 다르기 때문에 분할됩니다.따라서, 페르미 수준에서 전자 상태의 밀도는 반대 방향을 가리키는 스핀에 대해서도 다릅니다.다수 스핀 전자의 페르미 레벨은 SP 밴드 내에 있으며, 강자석과 비자성 금속에서 수송은 유사합니다.소수 스핀 전자의 경우 sp와 d밴드가 교배되며 페르미 수준은 d밴드 내에 있다.교배된 SPD 대역은 높은 밀도의 상태를 가지며, 이는 산란을 더 강하게 유발하며, 따라서 majority-spin 전자보다 manority-spin에 대한 평균 자유 경로 θ가 짧다.코발트 도프 니켈은 비θ_↑/θ가_↓ ^[23]20이 된다.

드루드 이론에 따르면, 얇은 금속막의 경우 전도율은 수 나노미터에서 수 나노미터에 이르는 δ에 비례합니다.전자는 평균 자유 경로를 크게 초과할 수 있는 소위 스핀 완화 길이(또는 스핀 확산 길이) 내에서 스핀 방향을 "기억"합니다.스핀 의존성 전송은 전하 캐리어의 스핀 방향에 대한 전기 전도도의 의존성을 나타냅니다.강자석에서는 미플릿 4s와 분할된 3d ^[7]밴드 사이의 전자 천이에 의해 발생합니다.

어떤 물질에서는, 전자와 원자 사이의 상호작용이 그들의 자기 모멘트가 평행하기 보다는 반평행일 때 가장 약하다.두 가지 유형의 재료를 조합하면 소위 역GMR ^[7][24]효과가 발생할 수 있습니다.

밴드 구조(왼쪽) 및 상태 밀도(오른쪽)

• 

  구리(비자성 금속).F – Fermi 레벨.수직 축은 에너지(eV)입니다.

• 

  코발트(메이저 스핀)

• 

  코발트(소수 스핀)

CIP 및 CPP 지오메트리

전류는 두 가지 방법으로 자기 초격자를 통과할 수 있습니다.Current in Plane(CIP) 지오메트리에서 전류는 층을 따라 흐르며 전극은 구조물의 한쪽에 위치합니다.전류 수직 평면(CPP) 구성에서는 전류가 층에 수직으로 통과하고 전극은 초격자의 다른 ^[7]쪽에 위치한다.CPP 지오메트리는 GMR이 2배 이상 높아지지만 실제로는 CIP ^[25][26]설정보다 실현하기 어렵습니다.

자기 초격자를 통한 캐리어 수송

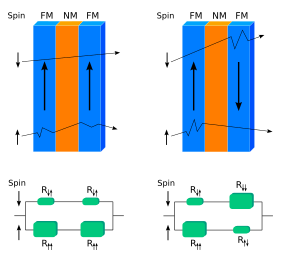
자기 순서는 층 간의 강자성 및 반강자성 상호작용에 따른 초격자에서 다릅니다.전자의 경우 인가된 자기장이 없는 다른 강자성층에서는 자화방향이 동일하지만 후자의 경우 다층에서는 반대방향이 번갈아 나타난다.강자성 초격자를 통과하는 전자는 회전 방향이 격자 자화와 반대일 때보다 격자 자화와 훨씬 더 약하게 상호작용합니다.이러한 이방성은 반강자성 초격자에 대해서는 관찰되지 않으며, 그 결과 강자성 초격자에 비해 강한 전자를 산란시켜 높은 전기 ^[7]저항을 나타낸다.

GMR 효과를 적용하려면 초격자 층의 평행 자화와 반평행 자화 사이의 동적 전환이 필요합니다.첫 번째 근사치에서는 비자성층으로 분리된 두 강자성층 간의 상호작용 에너지 밀도는 자화의 스칼라 곱에 비례합니다.

$(\displaystyle w=-J)(\mathbf {M} _{1}\cdot \mathbf {M} _{2}).}$

계수 J는 비자성층_s d의 두께에 대한 진동 함수이므로 J는 그 크기와 부호를 변경할 수 있습니다.d값이_s 반평행 상태에 해당하는 경우 외부 필드는 슈퍼래티스를 반평행 상태(고저항)에서 병렬 상태(저저항)로 전환할 수 있습니다.구조물의 총 저항은 다음과 같이 기술할 수 있습니다.

${\displaystyle R=R_{0}+\Delta R\sin ^{2}{\frac {\theta }{2}}$

여기서₀ R은 강자성 초격자의 저항, δR은 GMR 증분, δ는 인접층의 ^[25]자화 사이의 각도입니다.

수학적 설명

GMR 현상은 저항이 최소 또는 최대인 전자의 전도에 해당하는 두 개의 스핀 관련 전도성 채널을 사용하여 설명할 수 있습니다.이들 사이의 관계는 스핀 이방성 β의 계수로 정의되는 경우가 많다.이 계수는 다음과 같은 형태의 스핀 편파 전류에 대한 특정 전기 저항률 θ의_F± 최소 및 최대값을 사용하여 정의할 수 있습니다.

$\displaystyle \rho _{F\pm }=syslogfrac {2\rho _{F}}{1\pm \pm }}$

여기서 θ는_F 강자석의 ^[27]평균 저항률이다.

CIP 및 CPP 구조의 저항기 모델

강자성 금속과 비자성 금속의 계면에서의 전하 캐리어의 산란이 작고 전자 스핀의 방향이 충분히 오래 유지된다면 시료의 총저항이 자기층과 비자성층의 저항을 조합한 모델을 고려하는 것이 편리하다.

이 모델에서는 층의 자화와 관련하여 다양한 스핀 방향을 가진 전자에 대한 두 개의 전도 채널이 있습니다.따라서 GMR 구조의 등가회로는 각 채널에 대응하는 2개의 병렬접속부로 구성된다.이 경우 GMR은 다음과 같이 나타낼 수 있습니다.

$({displaystyle \parrow _{H}={Delta R}{Delta R}{\uparrow \downarrow }}) {R_{\uparrow \uparrow }}}=parc {{\rho_F+}-{{\h}) _frac {{\f}_{\f}_{\f}}$

여기서 R의 첨자는 층에서의 공선 및 반대방향 자화를 나타내고, θ = b/a는 자성층과 비금속층의 두께비, θ는_N 비금속계의 저항률을 나타낸다.이 표현은 CIP 구조 및 CPP 구조 모두에 적용할 수 있습니다.조건 $\chi {\displaystyle }$ ${\displaystyle N_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle F_{}}$ ± ${\$_{$N}\ll \rho$ _${F\pm}}$에서 이$$ 관계는 스핀 비대칭 계수를 사용하여 단순화할 수 있습니다.

${\displaystyle \displaystyle _{H}={frac ^{2}}{1-\displaystyle ^{2}}.}$

전자 스핀의 방향에 따라 저항이 발생하는 이러한 장치를 스핀 밸브라고 합니다.층의 자화가 평행하면 "열린" 상태이고 그렇지 않으면 "^[28]닫힌" 상태입니다.

Valet-Fert 모델

1993년 티에리 발렛과 알베르 페르는 볼츠만 방정식에 기초한 CPP 기하학의 거대 자기 저항 모델을 제시했습니다.이 모델에서 자성층 내부의 화학적 전위는 두 가지 기능으로 나뉘는데, 이는 층의 자화에 대해 스핀이 평행한 전자와 반평행하는 전자에 해당합니다.비자성층이 충분히 얇으면 외부장₀ E에서는 전기화학적 전위와 샘플 내부의 장에 대한 수정이 다음과 같이 됩니다.

$({displaystyle \Delta \mu = frac {1-\flac ^{2}})E_{0}\ell _{s}e^{z/\ell _{s}})$

$({displaystyle \Delta E=black {{2}} {1-\flac ^{2}} } E_{0} \ell _{s} e^{z/\ell _{s}} )$

여기서 θ는_s 스핀 완화의 평균 길이이며, z 좌표는 자기층과 비자기층 사이의 경계에서 측정됩니다(z < 0은 ^[18]강자성에 해당합니다).따라서 화학 전위가 큰 전자는 강자석의 ^[29]경계에 축적됩니다.이는 스핀 축적_AS V의 잠재력 또는 이른바 계면 저항(강자석과 비자성 물질 사이의 경계에 속함)으로 나타낼 수 있습니다.

$({displaystyle R_{i}=parac(\mu _{\uparrow \uparrow }-\mu _{\uparrow \uparrow }}){2ej}=parac {\ell _{n}\rho _{1+(1-\beta ^2\r})_ellF}\rho _{F}}},}$

여기서 j는 표본의 전류 밀도이고, θ는_sNsF 비금속 및 자성 재료의 스핀 완화 길이이다.^[30]

디바이스 준비

재료 및 실험 데이터

많은 재료 조합이 ^[31]GMR을 나타내며, 가장 일반적인 것은 다음과 같습니다.

• FeCr^[10]
• CoCu₁₀₉₀ : temper_H^[32] = 상온에서 40%
• [110]CoFe₉₅₅/Cu: 상온에서 ^[31]θ_H = 110%.

자기저항은 디바이스의 형상(CIP 또는 CPP), 온도, 강자성층과 비자성층의 두께 등 많은 파라미터에 따라 달라집니다.4.2K의 온도와 1.5nm의 코발트층 두께에서_Cu 구리층 d의 두께를 1~10nm로 늘리면 CIP 지오메트리에서 δ80%에서 10%로_H 감소한다.한편 CPP 기하학에서는 d = 2.5nm에 대해_Cu 최대 δ_H(125%)가 관찰되었으며, d를 10nm로 증가시키면_Cu 진동 방식으로 ^[33]δ가_H 60%로 감소하였다.

Co(1.2nm)/Cu(1.1nm) 초격자를 거의 0에서 300K로 가열했을 때 CIP 지오메트리에서는 40~20%, CPP ^[34]지오메트리에서는 100~55%로 감소했습니다_H.

비자성층은 비금속층일 수 있습니다.예를 들어 유기층에서는 11K에서 ^[35]▲40_H%까지 입증되었으며, 다양한 설계의 그래핀 스핀 밸브에서는 ▲7K에서 약 12%, 300K에서 약 10%로 이론적인_H 한계인 109%^[36]를 크게 밑돌았다.

GMR 효과는 특정 스핀 방향을 가진 전자를 선택하는 스핀 필터를 통해 향상될 수 있습니다. 이 필터는 코발트와 같은 금속으로 만들어집니다.두께 t 필터의 경우 전도율 δG의 변화는 다음과 같이 나타낼 수 있다.

$\displaystyle \Delta G=\Delta G_{SV}+\Delta G_{f}(1-e^{\beta t/\lambda}),}$

여기서 필터가 없는 스핀밸브의 전도율 변화_SV δG는 필터와의 전도율 최대 증가 δG_f, β는 필터재의 ^[37]파라미터이다.

GMR의 종류

GMR은 ^[38]영향을 미치는 디바이스 유형에 따라 분류되는 경우가 많습니다.

영화들

반강자성 초격자

필름의 GMR은 페르트와 그룬베르크에 의해 강자성층과 비자성층으로 구성된 초격자 연구에서 처음 관찰되었다.비자성 층의 두께는 층 간의 상호작용이 반강자성이고 인접한 자성 층의 자화가 반평행하도록 선택되었다.그러면 외부 자기장이 자화 벡터를 평행하게 만들어 구조물의 ^[10]전기 저항에 영향을 줄 수 있습니다.

이러한 구조의 자성층은 반강자성 결합을 통해 상호작용하며, 이는 비자성층의 두께에 대한 GMR의 진동 의존성을 초래한다.반강자성 초격자를 사용한 첫 번째 자기장 센서에서는 층(크롬, 철 또는 코발트로 구성됨) 간의 강한 반강자성 상호작용과 층 내 강한 이방성 때문에 포화장이 최대 수만 개까지 매우 컸다.그 때문에, 디바이스의 감도는 매우 낮았다.자성층에는 퍼머로이, 비자성층에는 은을 사용하여 포화장을 수십 ^[39]개로 낮췄다.

교환 바이어스를 이용한 스핀 밸브

가장 성공적인 스핀 밸브에서 GMR 효과는 교환 바이어스에서 비롯됩니다.그것들은 민감한 층, "고정" 층 및 반강자성 층으로 구성됩니다.마지막 층은 "고정" 층의 자화 방향을 동결합니다.구조물의 저항을 줄이기 위해 민감층과 반강자성층을 얇게 만듭니다.밸브는 "고정" ^[39]층에 상대적으로 민감한 층의 자화 방향을 변경하여 외부 자기장에 반응합니다.

다른 다층 GMR 장치와의 이러한 스핀 밸브의 주요 차이점은 비자성층의 두께_N d에 대한 효과 진폭의 단조로운 의존성이다.

$\displaystyle _{H}(d_{N})=\delta _{H0}{\frac {exp \left(-d_{N}/\lambda _{N}\right}}{1+d_{N}/d_{0}}}}$

여기서 θ는_H0 정규화 상수이고, θ는_N 비금속 물질에서 전자의 평균 자유 경로이며₀, d는 ^[38][40]층 간의 상호작용을 포함하는 유효 두께이다.강자성층의 두께에 대한 의존성은 다음과 같이 나타낼 수 있습니다.

$\displaystyle _{H}(d_{F})=\delta _{H1}{\frac {1-\exp \left(-d_{F}/\lambda _{F}\right){1+d_{F}/d_{0}}.}$

파라미터는 앞의 방정식과 같은 의미를 가지지만 현재는 강자성층을 ^[31]참조하고 있습니다.

비인터랙티브 멀티레이어(의사 오스핀 밸브)

GMR은 반강자성 결합층이 없는 경우에도 관찰될 수 있습니다.이 경우 자기저항은 보자기력의 차이로 인해 발생한다(예를 들어 코발트보다 퍼머로이 쪽이 작다).퍼머로이/Cu/Co/Cu 등의 다층에서는 외부 자기장이 포화 자화 방향을 강자계에서는 평행으로, 약자계에서는 반평행으로 전환한다.이러한 시스템은 반강자성 ^[39]결합이 있는 슈퍼래티스보다 낮은 포화장과 더 큰 µ를_H 나타낸다.Co/Cu 구조에서도 유사한 효과가 관찰된다.이러한 구조의 존재는 GMR이 층간 결합을 필요로 하지 않는다는 것을 의미하며, 외부 장에 ^[41]의해 제어될 수 있는 자기 모멘트의 분포에서 발생할 수 있습니다.

역GMR 효과

역GMR에서 저항은 층 내 자화의 반평행 배향에 대해 최소이다.자성층이 NiCr/Cu/Co/Cu와 같은 다른 물질로 구성되어 있을 때 역GMR이 관찰된다.스핀이 반대인 전자의 저항률은 $\delta {\displaystyle {}_{}}$ ${\displaystyle {\uparrow }_{}}$ , ${\displaystyle {}_{}}$ ${\displaystyle 2\frac{\mathrm{}}{}}$ ${\displaystyle \frac{{\delta }_{}}{}}$ F${\displaystyle \frac{}{{}_{}}}$ ±$$ {\$displaystyle \rho$ _${\uparrow ,\downarrow$ } =$δfrac {2\rho _{F}}{1\pm$ \pm$\}\}$로 표기할 수 있으며 스핀업 전자의 계수 β가 다르다.NiCr층이 너무 얇지 않으면 그 기여도가 Co층을 초과하여 역GMR이 발생할 ^[24]수 있다. GMR 반전은 인접한 강자성층에서 계수 β의 곱의 부호에 의존하지만 개별 ^[34]계수의 부호에 의존하지는 않는다.

NiCr 합금이 바나듐 도프 니켈로 대체되는 경우에도 역GMR이 관찰되지만, 니켈을 철, 코발트, 망간, 금 또는 ^[42]구리로 도핑하는 경우에는 관찰되지 않습니다.

입상 구조의 GMR

강자성 금속과 비자성 금속의 입상 합금의 GMR은 1992년에 발견되었고, 이후 표면과 입자 대부분에서 전하 운반체의 스핀 의존 산란으로 설명되었다.이 입자들은 비자성 금속에 직경 약 10 nm의 강자성 클러스터를 형성하여 일종의 초격자를 형성합니다.이러한 구조에서 GMR 효과를 위해 필요한 조건은 구성 요소(예: 코발트 및 구리)의 상호 용해성 저하입니다.이러한 특성은 측정 및 아닐 온도에 따라 크게 달라집니다.역GMR을 ^[32][43]나타낼 수도 있습니다.

적용들

스핀밸브 센서

일반원칙

GMR 소재의 주요 용도 중 하나는 하드 디스크^[25] 드라이브 및 바이오 ^[31]센서와 같은 자기장 센서와 MEMS의 ^[31]진동 검출기에 있습니다.일반적인 GMR 기반 센서는 7층으로 구성됩니다.

1. 실리콘 기판,
2. 바인더 레이어,
3. 감지(비고정) 레이어,
4. 비자성층,
5. 고정 레이어,
6. 반강자성(핀)층,
7. 보호층

바인더 및 보호층은 탄탈로 되어 있는 경우가 많으며, 전형적인 비자성 재료는 구리입니다.감지층에서는 외부 자기장에 의해 자화 방향을 변경할 수 있으며, 일반적으로 NiFe 또는 코발트 합금으로 구성됩니다.반강자성층에는 FeMn 또는 NiMn을 사용할 수 있다.고정된 층은 코발트와 같은 자성 물질로 만들어진다.이러한 센서는 자기적으로 단단한 고정층이 ^[44][45]존재하기 때문에 비대칭 히스테리시스 루프를 가지고 있습니다.

스핀 밸브는 이방성 자기 저항을 나타낼 수 있으며, 이는 감도 ^[46]곡선의 비대칭성을 초래할 수 있습니다.

하드 디스크 드라이브

하드디스크드라이브(HDD)에서는 정보는 자기 도메인을 사용하여 부호화되며, 그 자화방향의 변화는 논리레벨 1과 관련지어지며, 변경은 논리0을 나타내지 않는다.기록 방법에는 종방향과 수직방향의 두 가지가 있습니다.

종방향법은 표면에 대해 자화가 법선이다.자기장이 재료로부터 나오는 도메인간에 전이 영역(도메인 벽)을 형성한다.도메인 벽이 두 개의 북극 도메인의 인터페이스에 있는 경우 필드는 바깥쪽으로 향하고 두 개의 남극 도메인의 경우 내부로 향합니다.영역벽 위의 자기장 방향을 읽기 위해 반강자성층 표면에 대해 수직방향으로 고정하고 감지층 표면에 평행하게 한다.외부 자기장의 방향을 변경하면 감지층의 자화가 편향됩니다.자기장이 감지층과 고정층의 자화를 정렬하는 경향이 있으면 센서의 전기 저항이 감소하며 그 반대도 ^[47]마찬가지입니다.

자기 RAM

자기저항랜덤액세스메모리(MRAM) 셀은 스핀밸브센서와 유사한 구조를 가진다.저장된 비트의 값은 센서 층의 자화 방향을 통해 인코딩할 수 있습니다. 이 값은 구조의 저항을 측정하여 판독됩니다.이 테크놀로지의 장점은 전원으로부터의 독립성(자화 방향의 변경에 대한 잠재적인 장벽으로 인해 전원이 꺼졌을 때 정보가 유지됨), 저소비전력 및 ^[25]고속화입니다.

일반적인 GMR 기반의 기억장치에서 CIP 구조는 서로 수직인 2개의 배선 사이에 위치한다.이러한 도체를 행과 열의 선이라고 합니다.라인을 통과하는 전류의 펄스는 보텍스 자기장을 발생시켜 GMR 구조에 영향을 미칩니다.필드 라인은 타원체 모양을 가지며 필드 방향(시계 방향 또는 시계 반대 방향)은 라인 내 전류 방향에 따라 결정됩니다.GMR 구조에서 자화는 선을 따라 배향된다.

기둥의 라인에 의해 생성되는 자기장의 방향은 자기 모멘트와 거의 평행하여 방향을 바꿀 수 없습니다.행의 선은 수직이며, 필드의 크기에 관계없이 자화를 90°만 회전시킬 수 있습니다.행과 열 라인을 따라 펄스가 동시에 통과하면 GMR 구조 위치의 총 자기장은 한 점에 대해 예각으로, 다른 점에 대해서는 둔각으로 향한다.필드의 값이 일부 임계값을 초과하면 필드의 방향이 변경됩니다.

기재된 셀에는 몇 가지 저장 및 판독 방법이 있습니다.하나의 방법에서는 정보는 감지층에 저장되며, 이 정보는 저항 측정을 통해 읽혀지고 읽힐 때 지워진다.다른 방법에서는 정보는 고정층 내에 유지되며 읽기 ^[48]전류에 비해 높은 기록 전류를 필요로 한다.

터널 자기저항(TMR)은 스핀밸브 GMR의 확장으로 전자가 얇은 절연 터널 장벽(비철 자기 스페이서 대체)을 통해 층에 수직으로 스핀 방향을 잡고 이동합니다.이를 통해 더 큰 임피던스, 더 큰 자기저항값(상온에서 최대 10배) 및 무시할 수 있는 온도 의존성을 실현할 수 있습니다.TMR은 현재 MRAM과 디스크 드라이브의 GMR을 대체하고 있으며, 특히 높은 영역 밀도와 수직 ^[49]기록에서 GMR을 대체하고 있습니다.

기타 응용 프로그램

전기회로의 전기적으로 절연된 두 부분 간에 비접촉 신호 전송을 위한 자기저항 절연체는 광 절연체의 대안으로 1997년에 처음 입증되었다.4개의 동일한 GMR 디바이스의 휘트스톤 브릿지는 균일한 자기장에 민감하지 않으며 브리지의 인접 암에서 필드 방향이 반평행일 때만 반응합니다.이러한 장치는 2003년에 보고되었으며 선형 주파수 ^[31]응답을 가진 정류기로 사용될 수 있습니다.

메모들

인용문

참고 문헌

외부 링크

• 거대 자기 저항: 아주 작은 도구에 숨겨진 정말 큰 아이디어 국립 고자기장 연구소
• 2012년 1월 11일 Wayback Machine에서 GMR 테크놀로지 프레젠테이션(IBM Research) 아카이브