프란틀-마이어 확장 팬

초음속 흐름이 볼록한 코너에 부딪히면 팽창 팬을 형성하는데, 코너에 위치한 무한히 많은 팽창 파동으로 구성된다.이 그림은 그러한 이상적인 팽창 팬을 보여준다.

기술적으로 2차원 단순파인 Prandtl-Meyer expansion fan으로 알려진 초음속 팽창 팬은 초음속 흐름이 볼록한 코너를 돌 때 발생하는 중심 팽창 과정이다.선풍기는 마하파의 무한대수로 이루어져 있으며, 날카로운 모서리에서 갈라진다.흐름이 매끄럽고 둥근 모퉁이를 돌 때, 이러한 파도는 한 지점에서 만나기 위해 뒤로 뻗어나갈 수 있다.

팽창 팬의 각 파동은 흐름을 점진적으로(작은 걸음으로) 돌린다.단일 "충격" 파동을 통해 흐름이 바뀌는 것은 물리적으로 불가능하다. 이는 열역학 제2법칙에 위배되기 때문이다.^[1]

팽창 팬을 가로질러 흐름이 가속(속도 증가)하고 마하 수는 증가하는 반면 정압, 온도, 밀도는 감소한다.공정이 등방성이므로 정체 특성(예: 총 압력 및 총 온도)은 팬 전체에서 일정하게 유지된다.

이 이론은 테오도르 마이어가 1908년 자신의 논문 논문에 대해 1년 전에 이미 문제를 논의했던 그의 고문 루트비히 프란틀과 함께 서술한 것이다.^[2]^[3]

흐름 특성

팽창 팬은 무한 확장파 또는 마하 라인으로 구성된다.^[4]The first Mach line is at an angle $\mu _{1}=\arcsin \left({\frac {1}{M_{1}}}\right)$ with respect to the flow direction, and the last Mach line is at an angle $\mu _{2}=\arcsin \left({\frac {1}{M_{2}}}\right)$ with respect to최종 흐름 방향유량이 작은 각도로 회전하고 각 팽창파에 걸친 변화가 작기 때문에 전체 공정이 등방성이다.^[1]이것은 흐름 속성의 계산을 상당히 단순화시킨다. $\rho _{0}$ 이 등방성이기 때문에 정체 압력( $p_{0}$ p $p_{0}$ ${\$ 정체 온도( $T_{0}$ 0 {\ $displaystyle T_{0$ 정체 밀도( $\rho _{0}$ 0 {\ $displaystyle \rho_{0$ 와 같은 정체 특성이 일정하게 유지된다.최종 정적 속성은 최종 흐름 마하 수( $M_{2}$ 2 ${\$ }})의 함수로서 다음과 같은 초기 흐름 조건과 관련될 수 있으며, 여기서 $\gamma$ $\gamma$ 은 기체의 열 용량 비율(공기의 경우 1.4)이다 $\gamma$ .

{\begin{igned}{\frac {T_{2}}:{T_{1}}}&=\leftᆪ\\[3pt]{\frac{{2p_}}{p_{1}}}&=\left({\frac{1+{\frac{\gamma)}{2}}M_{1}^{2}}{1+{\frac{\gamma)}{2}}M_{2}^{2}}}\right)^{\frac{\gamma}{\gamma)}}\\[3pt]{\frac{\rho_{2}}{\rho_{1}}}&=\left({\frac{1+{\frac{\gamma)}{2}}M_{1}^{2}}.{1+{\frac{)감마 -1}{2}}M_{2}^{2}}}\오른쪽)^{\frac {1}{\gamma -1}.\end{정렬}}

턴 후의 마하 번호( $M_{2}$ 2 $M_{2}$ {\ $displaystyle M_{$ 2 $M_{2}$ )는 초기 마하 번호 $M_{1}$ 1 $M_{1}$ {\ $displaystyle M_{1$ }) 및 턴 각도( $display$ {\displaystyle \ $theta$ )와 관련이 있다.

\theta =\nu(M_{2})-\nu(M_{1})\,

여기서, $\nu (M)\,$ ( M $\nu (M)\,$ ) ${\$ 은 $\nu (M)\,$ (는) Prandtl-Meyer 함수다.이 함수는 소닉 흐름(M = 1)이 특정 마하 수(M)에 도달하기 위해 회전해야 하는 각도를 결정한다. 수학적으로,

{\begin{aligned}\nu (M)&=\int {\frac {\sqrt {M^{2}-1}}{1+{\frac {\gamma -1}{2}}M^{2}}}{\frac {\,dM}{M}}\\&={\sqrt {\frac {\gamma +1}{\gamma -1}}}\arctan {\sqrt {{\frac {\gamma -1}{\gamma +1}}\left(M^{2}-1\right)}}-\arctan {\sqrt {M^{2}-1}}.\\end{aigned}

관례상 $\nu (1)=0.\,$ ( $\nu (1)=0.\,$ ) $\nu (1)=0.\,$ = $\nu (1)=0.\,$ ${\$

Thus, given the initial Mach number ( $M_{1}$ ), one can calculate $\nu (M_{1})\,$ and using the turn angle find $\nu (M_{2})\,$ . From the value of $\nu (M_{2})\,$ one can obtain the final Mach number ( $M_{2}$ $M_{2}$ ) 및 기타 흐름 속성.

최대 턴 각도

초음속 흐름이 회전할 수 있는 최대 각도(

\theta _{\text{max}}

{\

에는 한계가 있다.

마하 숫자는 1에서 $\infty$ 까지 다양하므로 ${\displaystyle \infit },$ $\nu \,$ ${\$ \,}은(는) $\nu _{\text{max}}\,$ 에서 최대 $displaystyle \nu_{\text{max},}$ 까지의 값을 $\nu \,$ 취한다 $\nu _{\text{max}}\,$

\nu _{\text{max}={\frac {\pi }{2}}\좌측\sqrt {\fract {\frac {\frac}{\frac -1}-1\우측).

이것은 초음속 흐름이 얼마나 많이 회전할 수 있는가에 제한을 두고, 최대 회전 각도는 다음과 같다.

\theta _{\text{max}=\nu _{\text{max}-\nu(M_{1})\,

또한 다음과 같이 볼 수 있다.흐름은 경계 조건을 만족시킬 수 있도록 회전해야 한다.이상적인 흐름에서는, 흐름이 충족시켜야 하는 두 종류의 경계 조건이 있다.

속도 경계 조건 - 벽에 대한 유속 구성 요소가 0임을 나타낸다.그것은 또한 침입금지 경계조건으로도 알려져 있다.
(흐름에 충격이 없기 때문에) 흐름 내부의 정압에 불연속성이 있을 수 없다는 것을 나타내는 압력 경계 조건.

흐름이 벽과 평행해질 정도로 돌면 압력경계조건에 대해 걱정할 필요가 없다.그러나 유량이 회전함에 따라 (앞서 설명한 바와 같이) 정압은 감소한다.시작하기에 충분한 압력이 없으면 흐름이 회전을 완료할 수 없고 벽에 평행하지 않게 된다.이것은 흐름이 회전할 수 있는 최대 각도로 나타난다.마하 수치가 낮을수록( $M_{1}$ 즉, 작은 $M_{1}$ $M_{1}$ ${\$ 흐름이 회전할 수 있는 최대 각도가 커진다.

최종 흐름 방향과 벽을 구분하는 능률화는 슬립스트림(그림에서 점선으로 표시됨)으로 알려져 있다.이 선에 걸쳐 속도의 온도, 밀도 및 접선 성분의 점프가 있다(정상 성분은 0이다).슬립스트림 너머로는 흐름이 정체된다(벽의 속도 경계 조건을 자동으로 만족함).실제 흐름의 경우 추가적인 미끄럼 방지 경계 조건 때문에 슬립스트림 대신 전단 층이 관찰된다.

메모들

^ ^a ^b

단일 "충격"을 통한 확장 과정은 불가능하며, 이는 열역학 제2법칙을 위반하기 때문이다.

단일 "충격" 파동을 통한 흐름 확장 불가능: 인접한 그림에 나타난 시나리오를 고려한다.초음속 흐름이 회전함에 따라 속도의 정상 성분( $w_{2}>w_{1}$ $w_{2}>w_{1}$ > w $w_{2}>w_{1}$ ${\$ }:{1 $})$ 은 증가하는 반면 접선성분은 일정하게 유지된다( $v_{2}=v_{1}$ 2 $v_{2}=v_{1}$ = $v_{2}=v_{1}$ $v_{2}=v_{1}$ ${\$ }). $v_{2}=v_{1}$ 해당 변화는 엔트로피( $\Delta s=s_{2}-s_{1}$ $\Delta s=s_{2}-s_{1}$ = $\Delta s=s_{2}-s_{1}$ $\Delta s=s_{2}-s_{1}$ - $\Delta s=s_{2}-s_{1}$ $\Delta s=s_{2}-s_{1}$ ${\$ 로 표현할 수 있다 $\Delta s=s_{2}-s_{1}$

${\begin{aligned}{\frac {\Delta s}{R}}&=\ln \left[\left({\frac {p_{2}}{p_{1}}}\right)^{\frac {1}{\gamma -1}}\left({\frac {\rho _{2}}{\rho _{1}}}\right)^{-{\frac {\gamma }{\gamma -1}}}\right]\\&\approx {\frac {\gamma +1}{12\gamma ^{2}}}\left({\frac {p_{2}-p_{1}}{p_{1}}}\right)^{3}\\&\approx {\frac {\gamma +1}{12\gamma ^{2}}}\left[{\frac {\rho _{1}w_{1}^{2}}{p_{1}}}\left(1-{\frac {w_{2}}{w_{1}}}\right)\right]^{3}\end{aligned}}$

여기서, $R$ $R$ 은 $R$ (는) 범용 가스 $\gamma$ , $\rho$ $display$ {\displaystyle $\rho$ $\gamma$ }은(는) 특정 열 $\rho$ 의 비율, $display$ {\ $displaystyle$ \rho $\rho$ $}$ 은(는 $p$ ) $정적$ 압력 $,$ s {\ $displaystysty$ s $}$ 은 엔트로피 $s$ , w $}$ 은 흐름의 구성 요소다 $w$ ."속도"에 대한 정상 속도.접미사 "1"과 "2"는 각각 초기 조건과 최종 조건을 가리킨다.
$w_{2}>w_{1}$ $w_{2}>w_{1}$ > $w_{2}>w_{1}$ $w_{2}>w_{1}$ ${\$ 1} 이후 $w_{2}>w_{1}$ 이는 $\Delta s<0$ < $\Delta s<0$ {\ $displaystyle \Delta s <0$ 이것이 가능하지 않기 때문에 하나의 충격파를 통해 흐름을 돌릴 수 없다는 것을 의미한다.한계 $\Delta s\rightarrow 0$ → $[\displaystyle \Delta s\오른쪽$ 화살표 $0}$ 에서 무한히 많은 수의 팽창파를 통한 회전을 고려할 때에만 그러한 팽창 과정이 발생할 수 있다는 것을 보여주기 위해 이 주장은 더 확장될 수 있다 $\Delta s\rightarrow 0$ 따라서 팽창 과정은 등방성 과정이다.
^ Meyer, T. (1908). Über zweidimensionale Bewegungsvorgänge in einem Gas, das mit Überschallgeschwindigkeit strömt (Doctoral dissertation) (in German). Georg-August Universität, Göttingen. OCLC 77709738.
^ Prandtl, L. (1907). "Neue Untersuchungen über die strömende Bewegung der Gase und Dämpfe". Physikalische Zeitschrift (in German). 8: 23–30. 다시 인쇄됨
^

A지점에서 B지점(거리 u·t)으로 이동할 때 $u>c$ ( $u>c$ $u>c$ c ${\displaystyle u>c$ 으로 이동하는 물체의 경우 A지점에서 발생하는 교란은 거리 c·t를 이동한다.해당 각도는 마하 각도로 알려져 있으며, 교란된 영역을 둘러싸는 선은 마하선(2-D 케이스) 또는 마하콘(3-D)으로 알려져 있다.
마하 선(코인) 및 마하 각도:
마하 선은 보통 2-D 초음속 흐름에서 만나는 개념이다(예: $M\geq 1$ 1 $[\displaystyle M\geq 1$ }). $M\geq 1$ 그것들은 한 쌍의 경계선으로서 방해받지 않는 흐름과 방해받지 않는 흐름을 구분한다.이 선들은 쌍으로 발생하며 각도로 방향을 정한다.

$\mu =\arcsin \왼쪽({\frac {c}{u}\오른쪽)=\arcsin \왼쪽({\frac {1}{M}\오른쪽)$

운동 방향(마하 각도라고도 한다)에 관하여.3-D 유동장의 경우, 이 선들은 마하 원뿔이라고 알려진 표면을 형성하며, 마하 각은 원뿔의 반각으로 한다.
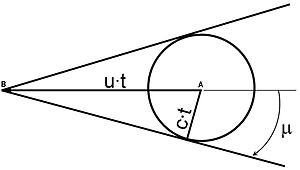
개념을 더 잘 이해하려면 그림에서 스케치된 사례를 고려하십시오.우리는 물체가 흐름 속에서 움직일 때 압력 장애를 일으킨다는 것을 안다.그림에는 초음속 $u>c$ > c ${\displaystyle u>c})$ 에서 선 AB를 따라 A지점에서 B지점으로 이동하는 물체가 표시된다. $u>c$ 물체가 지점 B에 도달할 때까지 지점 A로부터의 압력 장애는 거리 c/t를 이동했고 이제 원의 둘레에 있다(점 A에 중심이 있음).AB 선에 중심이 있는 무한의 그런 원들이 있는데, 각각은 물체의 움직임으로 인한 장애의 위치를 나타낸다.점 B에서 바깥쪽으로 전파되고 이 원들에 접하는 선은 마하 선이라고 알려져 있다.
참고: 이러한 개념은 초음속 $u\geq c$ (u $u\geq c$ have c {\ $displaystyle u\geq c})$ 에 대해서만 물리적 의미를 갖는다.아음속 흐름의 경우 교란이 소스보다 빠르게 이동하며 $\arcsin()$ in $\arcsin()$ ( $\arcsin()$ ) $\arcsin()$ 함수의 $\arcsin()$ 인수가 1보다 클 것이다.

참고 항목

참조

Liepmann, Hans W.; Roshko, A. (2001) [1957]. Elements of Gasdynamics. Dover Publications. ISBN 0-486-41963-0.
Von Mises, Richard (2004) [1958]. Mathematical theory of compressible fluid flow. Dover Publications. ISBN 0-486-43941-0.
Courant, Richard; Friedrichs, K. O. (1999) [1948]. Supersonic flow and shock waves. Springer Science+Business Media. ISBN 0387902325.
Anderson, John D. Jr. (January 2001) [1984]. Fundamentals of Aerodynamics (3rd ed.). McGraw-Hill Science/Engineering/Math. ISBN 0-07-237335-0.
Shapiro, Ascher H. (1953). The Dynamics and Thermodynamics of Compressible Fluid Flow, Volume 1. Ronald Press. ISBN 978-0-471-06691-0.

외부 링크

팽창 팬(NASA)
Prandtl-Meyer 확장 팬 계산기(Java 애플릿).

[shockExpansion-1] 

단일 "충격"을 통한 확장 과정은 불가능하며, 이는 열역학 제2법칙을 위반하기 때문이다.

단일 "충격" 파동을 통한 흐름 확장 불가능: 인접한 그림에 나타난 시나리오를 고려한다.초음속 흐름이 회전함에 따라 속도의 정상 성분( $w_{2}>w_{1}$ $w_{2}>w_{1}$ > w $w_{2}>w_{1}$ ${\$ }:{1 $})$ 은 증가하는 반면 접선성분은 일정하게 유지된다( $v_{2}=v_{1}$ 2 $v_{2}=v_{1}$ = $v_{2}=v_{1}$ $v_{2}=v_{1}$ ${\$ }). $v_{2}=v_{1}$ 해당 변화는 엔트로피( $\Delta s=s_{2}-s_{1}$ $\Delta s=s_{2}-s_{1}$ = $\Delta s=s_{2}-s_{1}$ $\Delta s=s_{2}-s_{1}$ - $\Delta s=s_{2}-s_{1}$ $\Delta s=s_{2}-s_{1}$ ${\$ 로 표현할 수 있다 $\Delta s=s_{2}-s_{1}$

${\begin{aligned}{\frac {\Delta s}{R}}&=\ln \left[\left({\frac {p_{2}}{p_{1}}}\right)^{\frac {1}{\gamma -1}}\left({\frac {\rho _{2}}{\rho _{1}}}\right)^{-{\frac {\gamma }{\gamma -1}}}\right]\\&\approx {\frac {\gamma +1}{12\gamma ^{2}}}\left({\frac {p_{2}-p_{1}}{p_{1}}}\right)^{3}\\&\approx {\frac {\gamma +1}{12\gamma ^{2}}}\left[{\frac {\rho _{1}w_{1}^{2}}{p_{1}}}\left(1-{\frac {w_{2}}{w_{1}}}\right)\right]^{3}\end{aligned}}$

여기서, $R$ $R$ 은 $R$ (는) 범용 가스 $\gamma$ , $\rho$ $display$ {\displaystyle $\rho$ $\gamma$ }은(는) 특정 열 $\rho$ 의 비율, $display$ {\ $displaystyle$ \rho $\rho$ $}$ 은(는 $p$ ) $정적$ 압력 $,$ s {\ $displaystysty$ s $}$ 은 엔트로피 $s$ , w $}$ 은 흐름의 구성 요소다 $w$ ."속도"에 대한 정상 속도.접미사 "1"과 "2"는 각각 초기 조건과 최종 조건을 가리킨다.
$w_{2}>w_{1}$ $w_{2}>w_{1}$ > $w_{2}>w_{1}$ $w_{2}>w_{1}$ ${\$ 1} 이후 $w_{2}>w_{1}$ 이는 $\Delta s<0$ < $\Delta s<0$ {\ $displaystyle \Delta s <0$ 이것이 가능하지 않기 때문에 하나의 충격파를 통해 흐름을 돌릴 수 없다는 것을 의미한다.한계 $\Delta s\rightarrow 0$ → $[\displaystyle \Delta s\오른쪽$ 화살표 $0}$ 에서 무한히 많은 수의 팽창파를 통한 회전을 고려할 때에만 그러한 팽창 과정이 발생할 수 있다는 것을 보여주기 위해 이 주장은 더 확장될 수 있다 $\Delta s\rightarrow 0$ 따라서 팽창 과정은 등방성 과정이다.

[2] Meyer, T. (1908). Über zweidimensionale Bewegungsvorgänge in einem Gas, das mit Überschallgeschwindigkeit strömt (Doctoral dissertation) (in German). Georg-August Universität, Göttingen. OCLC 77709738.

[3] Prandtl, L. (1907). "Neue Untersuchungen über die strömende Bewegung der Gase und Dämpfe". Physikalische Zeitschrift (in German). 8: 23–30. 다시 인쇄됨

[4] 

A지점에서 B지점(거리 u·t)으로 이동할 때 $u>c$ ( $u>c$ $u>c$ c ${\displaystyle u>c$ 으로 이동하는 물체의 경우 A지점에서 발생하는 교란은 거리 c·t를 이동한다.해당 각도는 마하 각도로 알려져 있으며, 교란된 영역을 둘러싸는 선은 마하선(2-D 케이스) 또는 마하콘(3-D)으로 알려져 있다.
마하 선(코인) 및 마하 각도:
마하 선은 보통 2-D 초음속 흐름에서 만나는 개념이다(예: $M\geq 1$ 1 $[\displaystyle M\geq 1$ }). $M\geq 1$ 그것들은 한 쌍의 경계선으로서 방해받지 않는 흐름과 방해받지 않는 흐름을 구분한다.이 선들은 쌍으로 발생하며 각도로 방향을 정한다.

$\mu =\arcsin \왼쪽({\frac {c}{u}\오른쪽)=\arcsin \왼쪽({\frac {1}{M}\오른쪽)$

운동 방향(마하 각도라고도 한다)에 관하여.3-D 유동장의 경우, 이 선들은 마하 원뿔이라고 알려진 표면을 형성하며, 마하 각은 원뿔의 반각으로 한다.
개념을 더 잘 이해하려면 그림에서 스케치된 사례를 고려하십시오.우리는 물체가 흐름 속에서 움직일 때 압력 장애를 일으킨다는 것을 안다.그림에는 초음속 $u>c$ > c ${\displaystyle u>c})$ 에서 선 AB를 따라 A지점에서 B지점으로 이동하는 물체가 표시된다. $u>c$ 물체가 지점 B에 도달할 때까지 지점 A로부터의 압력 장애는 거리 c/t를 이동했고 이제 원의 둘레에 있다(점 A에 중심이 있음).AB 선에 중심이 있는 무한의 그런 원들이 있는데, 각각은 물체의 움직임으로 인한 장애의 위치를 나타낸다.점 B에서 바깥쪽으로 전파되고 이 원들에 접하는 선은 마하 선이라고 알려져 있다.
참고: 이러한 개념은 초음속 $u\geq c$ (u $u\geq c$ have c {\ $displaystyle u\geq c})$ 에 대해서만 물리적 의미를 갖는다.아음속 흐름의 경우 교란이 소스보다 빠르게 이동하며 $\arcsin()$ in $\arcsin()$ ( $\arcsin()$ ) $\arcsin()$ 함수의 $\arcsin()$ 인수가 1보다 클 것이다.

[1]

[2]

[3]

[4]

Search

프란틀-마이어 확장 팬

네임스페이스

더

목차

흐름 특성

최대 턴 각도

메모들

참고 항목

참조

외부 링크