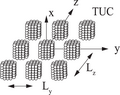
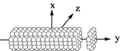
이산 쌍극자 근사

Discrete dipole approximation
이산 쌍극자 근사에서는 이산 방사 전기 쌍극자의 관점에서 더 큰 물체를 근사한다.

이산 쌍극자 근사(DDA)는 커플링 쌍극자 [1]근사라고도 하며 임의의 형상의 입자와 주기적인 구조에 의한 방사선의 산란을 계산하는 방법이다.임의의 기하학의 대상이 주어졌을 때, 사람들은 분극 가능한 작은 쌍극자의 유한 배열에 의한 연속체 목표물의 근사치에 의해 그것의 산란과 흡수 특성을 계산하려고 한다.이 기술은 나노포토닉스, 레이더 산란, 에어로졸 물리학 및 천체 물리학 등 다양한 응용 분야에 사용됩니다.

기본 개념

DDA의 기본 개념은 1964년 DeVoe에[2] 의해 분자 골재의 광학 특성을 연구하기 위해 DDA를 도입하였다. 지연 효과는 포함되지 않았기 때문에 DeVoe의 처리는 파장에 비해 작은 골재로 제한되었다.지연 효과를 포함한 DDA는 1973년 Purcell과 Pennypacker에[3] 의해 제안되었으며, 그는 이를 사용하여 성간 먼지 입자를 연구했다.간단히 말해서, DDA는 분극 가능한 점의 유한 배열에 의한 연속체 목표물의 근사치이다.이 지점들은 국소 전기장에 반응하여 쌍극자 모멘트를 획득합니다.쌍극자는 전기장을 통해 서로 상호작용하기 때문에 DDA는 결합 쌍극자 [1][4]근사라고도 합니다.

때가 있는 자연-1909년에 Lorentz[5]은 물질의 유전 성질에서 직접 중이죠. 작곡된 것은 개별적인 원자의 polarizabilities에, 특히, 정확한 단순한 관계는 클라우시우스 모소티 관계식(또는 Lorentz-Lorenz)과 관련된 것이 가능하다는 WTO도하 개발 아젠다를 위해 물리적인 영감을 제공한다 l.안데스 괭이밥정육면체 격자에 있는 테드.고체의 연속체 표현이 원자간 간격에 비해 큰 길이 척도에 적합하듯이, 분극 가능한 점의 배열은 다이폴 간 분리에 비해 큰 길이 척도에 연속체 목표물의 반응을 정확하게 근사할 수 있다고 기대할 수 있다.

점 쌍극자의 유한 배열에 대해 산란 문제는 정확히 해결될 수 있으므로, DDA에 존재하는 유일한 근사치는 연속체 표적을 N점 쌍극자의 배열로 대체하는 것이다.치환에는 지오메트리(쌍극자 위치)와 쌍극자 분극성의 사양이 필요합니다.단색 입사파의 경우 진동 쌍극자 모멘트에 대한 자기 일관성 해법을 찾을 수 있다. 이로부터 흡수 및 산란 단면이 계산된다.입사파의 2개의 독립된 편광에 대해 DDA 솔루션을 얻을 경우 완전한 진폭 산란 행렬을 결정할 수 있다.또는 DDA는 [6]전계에 대한 부피적분방정식에서 도출할 수 있다.이것은 포인트 쌍극자의 근사치가 적분 방정식의 이산화와 동등하며, 따라서 쌍극자 크기가 감소함에 따라 감소한다는 것을 강조한다.

분극성이 텐서일 수 있다는 인식으로 DDA는 이방성 재료에 쉽게 적용할 수 있다.자화율이 0이 아닌 물질을 처리하기 위한 DDA의 확장도 간단하지만, 대부분의 경우 자성 효과는 무시할 수 있다.

내선번호

이 방법은 DDA에서 발생하는 컨볼루션 문제를 계산하기 위해 고속 푸리에 변환을 적용한 드레인, 플라타우 및 굿맨에 의해 개선되었으며, 이는 큰 표적에 의한 산란을 계산할 수 있게 했다.그들은 이산 쌍극자 근사 오픈 소스 코드 DDSCAT를 [7][8]배포했다.현재 평면 [10][11]기판 위 또는 근처에 배치된 정기 목표물[9] 및 입자에 대한 확장 등 몇 가지 DDA [6]구현이 있습니다.정확한 기술과의 비교가 [12]발표되었습니다.이산 쌍극자 근사치의[13] 유효성 기준과 같은 다른 측면이 발표되었다.또한 DDA는 직사각형 또는 직육면체 쌍극자를 사용하도록 확장되었으며, 이는 매우 타원형 또는 프롤레이트 입자에 더 효율적입니다.

이산 쌍극자 근사 코드

리뷰와 기존 [12]코드의 비교 공개가 있습니다[7][6].대부분의 코드는 자유 공간 또는 균질 유전체 호스트 매체의 임의 형상 비자기 입자 및 입자 시스템에 적용된다.계산된 수량에는 일반적으로 뮐러 행렬, 적분 단면(소멸, 흡수 및 산란), 내부장 및 각도 분해 산란장(위상 함수)이 포함된다.

범용 오픈 소스 DDA 코드

이러한 코드는 일반적으로 정규 그리드(입방체 또는 직사각형 입방체), 선형 방정식의 큰 시스템을 풀기 위한 켤레 그라데이션 방법 및 컨볼루션 정리를 사용하는 행렬 벡터 곱의 FFT 가속도를 사용합니다.이 접근방식의 복잡성은 시간과 메모리 [6]쌍극자 수에서 거의 선형이다.

이름. 작가들 레퍼런스 언어 갱신필 특징들
DDSCAT 드레인 및 플랫아우 [7] 포트란 2019년 (7.3.3 버전) 또한 주기적인 입자를 처리하고 근거리장을 효율적으로 계산할 수 있습니다.OpenMP 액셀러레이션을 사용합니다.
DDscat.C++ 촐리 [15] C++ 2017년 (7.3.1 버전) C++로 변환된 DDSCAT 버전.몇 가지 기능이 더 향상되었습니다.
추가 Yurkin, Hoekstra 및 기고자 [16][17] C 2020 (1.4.0 버전) 평면 기판을 빠르고 엄격하게 검토하여 직사각형 큐보이드 복셀을 고도로 타원형 또는 프롤레이트 입자에 사용할 수 있습니다.또한 포인트 이미터의 배출량(감소율) 향상도 계산할 수 있습니다.근거리 계산은 그다지 효율적이지 않습니다.MPI(Message Passing Interface) 병렬화를 사용하여 GPU(OpenCL)에서 실행할 수 있습니다.
OpenDDA 맥도날드 [18][19] C 2009년 (0.4.1 버전) OpenMP와 MPI 병행화를 모두 사용합니다.계산 효율에 초점을 맞춥니다.
DDA-GPU 키에★ [20] C++ 2016 GPU(OpenCL) 상에서 동작합니다.알고리즘은 부분적으로 ADDA에 기초하고 있습니다.
VIE-FFT 샤 [21] C/C++ 2019 또한 근거리장과 재료 흡수율도 계산합니다.이름은 다르지만 알고리즘은 주류 DDA에서 사용되는 알고리즘과 매우 유사합니다.
복스 산란 그로트, 폴리메리디스, 화이트 [22] 매트랩 2019 반복 솔버를 가속하기 위해 순환제 프리 컨디셔너를 사용합니다.
IF-DDA 쇼멧, 센테낙 및 센테낙 [23] Fortran, Qt를 사용하는 C++의 GUI 2021 (0.6.23 버전) 바보 같은 DDA.OpenMP 및 HDF5를 사용합니다.다층 기판용 별도 버전(IF-DDAM)이 있습니다.
MPDDA 샤바닌자드, 아완, 라마크리슈나 [24] 매트랩 2021 (1.0 버전) GPU 상에서 실행(Matlab 기능 사용)

특수 DDA 코드

이 목록에는 이전 섹션에 적합하지 않은 코드가 포함되어 있습니다.원인은 다음과 같습니다. 소스 코드를 사용할 수 없거나 FFT 가속이 없거나 감소하며, 코드는 표준 산란량을 쉽게 계산할 수 없는 특정 애플리케이션에 초점을 맞춥니다.

이름. 작가들 레퍼런스 언어 갱신필 특징들
DDSURF, DDSUB, DDFILM 슈멜, 네베커, 장 [10][25][26] 포트란 2008 반무한 기판 및 유한 필름(임의의 입자 배치 포함)의 엄격한 취급. 단, 2D FFT 가속만 사용됩니다.
DDMM 마코우스키 [27] 포트란 2002 T 행렬을 계산하여 방향 평균 산란 특성을 효율적으로 계산할 수 있습니다.
CDA 맥마흔 [28] 매트랩 2006
DDA-SI 로케 [29] 매트랩 2014년 (0.2 버전) 기판을 엄격하게 취급하지만 FFT 가속은 사용되지 않습니다.
PyDDA 드미트리예프 파이썬 2015 DDA-SI의 재실장
e-DDA 바시요와 비겔로 [30] 포트란 2019년 (v.2.0) 전자 에너지 손실 분광법 및 음극 발광 시뮬레이션.DDSCAT 7.1을 기반으로 구축되었습니다.
드라이브 게우케트, 기욤, 헨라드 [31] 포트란 2013년 (v. 2.1) 전자 에너지 손실 분광법 및 음극 발광 시뮬레이션.영상 근사치를 통해 기판을 처리하지만 FFT 가속이 사용되지 않습니다.
T-DDA 에달라투르 [32] 포트란 2015 근거리 복사 열 전달을 시뮬레이션합니다.계산 병목 현상은 직접 매트릭스 반전입니다(FT 가속은 사용되지 않음).OpenMP 및 MPI 병렬화를 사용합니다.
CDDA 로잘레스, 알벨라, 곤살레스, 구티에레스, 모레노 [33] 2021 키랄 시스템(전기장과 자기장에 대한 결합 방정식을 해결)에 적용됩니다.

도형 갤러리

  • Scattering by periodic structures such as slabs, gratings, of periodic cubes placed on a surface, can be solved in the discrete dipole approximation.

    표면에 배치된 주기적인 큐브의 슬래브, 격자와 같은 주기적인 구조에 의한 산란을 이산 쌍극자 근사치로 해결할 수 있다.

  • Scattering by infinite object (such as cylinder) can be solved in the discrete dipole approximation.

    이산 쌍극자 근사에서는 무한 객체(원통 등)에 의한 산란을 해결할 수 있다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ a b Singham, Shermila B.; Salzman, Gary C. (1986). "Evaluation of the scattering matrix of an arbitrary particle using the coupled dipole approximation". J. Chem. Phys. AIP Publishing. 84 (5): 2658–2667. Bibcode:1986JChPh..84.2658S. doi:10.1063/1.450338.
  2. ^ DeVoe, Howard (1964-07-15). "Optical Properties of Molecular Aggregates. I. Classical Model of Electronic Absorption and Refraction". J. Chem. Phys. AIP Publishing. 41 (2): 393–400. Bibcode:1964JChPh..41..393D. doi:10.1063/1.1725879.
  3. ^ E. M. Purcell; C. R. Pennypacker (1973). "Scattering and absorption of light by nonspherical dielectric grains". Astrophys. J. 186: 705. Bibcode:1973ApJ...186..705P. doi:10.1086/152538.
  4. ^ Singham, Shermila Brito; Bohren, Craig F. (1987-01-01). "Light scattering by an arbitrary particle: a physical reformulation of the coupled dipole method". Opt. Lett. The Optical Society. 12 (1): 10–12. Bibcode:1987OptL...12...10S. doi:10.1364/ol.12.000010. PMID 19738776.
  5. ^ H. A. 로렌츠, 전자 이론 (튜브너, 라이프치히, 1909)
  6. ^ a b c d M. A. Yurkin; A. G. Hoekstra (2007). "The discrete dipole approximation: an overview and recent developments" (PDF). J. Quant. Spectrosc. Radiat. Transfer. 106 (1–3): 558–589. arXiv:0704.0038. Bibcode:2007JQSRT.106..558Y. doi:10.1016/j.jqsrt.2007.01.034. S2CID 119572857.
  7. ^ a b c Draine, B.T.; P.J. Flatau (1994). "Discrete dipole approximation for scattering calculations". J. Opt. Soc. Am. A. 11 (4): 1491–1499. Bibcode:1994JOSAA..11.1491D. doi:10.1364/JOSAA.11.001491.
  8. ^ B. T. Draine; P. J. Flatau (2008). "The discrete dipole approximation for periodic targets: theory and tests". J. Opt. Soc. Am. A. 25 (11): 2693–3303. arXiv:0809.0338. Bibcode:2008JOSAA..25.2693D. doi:10.1364/JOSAA.25.002693. PMID 18978846. S2CID 15747060.
  9. ^ Chaumet, Patrick C.; Rahmani, Adel; Bryant, Garnett W. (2003-04-02). "Generalization of the coupled dipole method to periodic structures". Phys. Rev. B. American Physical Society (APS). 67 (16): 165404. arXiv:physics/0305051. Bibcode:2003PhRvB..67p5404C. doi:10.1103/physrevb.67.165404. S2CID 26726283.
  10. ^ a b Schmehl, Roland; Nebeker, Brent M.; Hirleman, E. Dan (1997-11-01). "Discrete-dipole approximation for scattering by features on surfaces by means of a two-dimensional fast Fourier transform technique". J. Opt. Soc. Am. A. The Optical Society. 14 (11): 3026–3036. Bibcode:1997JOSAA..14.3026S. doi:10.1364/josaa.14.003026.
  11. ^ M. A. Yurkin; M. Huntemann (2015). "Rigorous and fast discrete dipole approximation for particles near a plane interface" (PDF). The Journal of Physical Chemistry C. 119 (52): 29088–29094. doi:10.1021/acs.jpcc.5b09271.
  12. ^ a b Penttilä, Antti; Zubko, Evgenij; Lumme, Kari; Muinonen, Karri; Yurkin, Maxim A.; et al. (2007). "Comparison between discrete dipole implementations and exact techniques". J. Quant. Spectrosc. Radiat. Transfer. Elsevier BV. 106 (1–3): 417–436. Bibcode:2007JQSRT.106..417P. doi:10.1016/j.jqsrt.2007.01.026.
  13. ^ Zubko, Evgenij; Petrov, Dmitry; Grynko, Yevgen; Shkuratov, Yuriy; Okamoto, Hajime; et al. (2010-03-04). "Validity criteria of the discrete dipole approximation". Appl. Opt. The Optical Society. 49 (8): 1267–1279. Bibcode:2010ApOpt..49.1267Z. doi:10.1364/ao.49.001267. hdl:2115/50065. PMID 20220882.
  14. ^ D. A. Smunev; P. C. Chaumet; M. A. Yurkin (2015). "Rectangular dipoles in the discrete dipole approximation" (PDF). J. Quant. Spectrosc. Radiat. Transfer. 156: 67–79. Bibcode:2015JQSRT.156...67S. doi:10.1016/j.jqsrt.2015.01.019.
  15. ^ V. Y. Choliy (2013). "The discrete dipole approximation code DDscat.C++: features, limitations and plans". Adv. Astron. Space Phys. 3: 66–70. Bibcode:2013AASP....3...66C.
  16. ^ M. A. Yurkin; V. P. Maltsev; A. G. Hoekstra (2007). "The discrete dipole approximation for simulation of light scattering by particles much larger than the wavelength" (PDF). J. Quant. Spectrosc. Radiat. Transfer. 106 (1–3): 546–557. arXiv:0704.0037. Bibcode:2007JQSRT.106..546Y. doi:10.1016/j.jqsrt.2007.01.033. S2CID 119574693.
  17. ^ M. A. Yurkin; A. G. Hoekstra (2011). "The discrete-dipole-approximation code ADDA: capabilities and known limitations" (PDF). J. Quant. Spectrosc. Radiat. Transfer. 112 (13): 2234–2247. Bibcode:2011JQSRT.112.2234Y. doi:10.1016/j.jqsrt.2011.01.031.
  18. ^ J. McDonald; A. Golden; G. Jennings (2009). "OpenDDA: a novel high-performance computational framework for the discrete dipole approximation". Int. J. High Perf. Comp. Appl. 23 (1): 42–61. arXiv:0908.0863. Bibcode:2009arXiv0908.0863M. doi:10.1177/1094342008097914. S2CID 10285783.
  19. ^ J. McDonald (2007). OpenDDA - a novel high-performance computational framework for the discrete dipole approximation (PDF) (PhD). Galway: National University of Ireland.
  20. ^ M. Zimmermann; A. Tausendfreund; S. Patzelt; G. Goch; S. Kieß; M. Z. Shaikh; M. Gregoire; S. Simon (2012). "In-process measuring procedure for sub-100 nm structures". J. Laser Appl. 24 (4): 042010. Bibcode:2012JLasA..24d2010Z. doi:10.2351/1.4719936.
  21. ^ W. E. I. Sha; W. C. H. Choy; Y. P. Chen; W. C. Chew (2011). "Optical design of organic solar cell with hybrid plasmonic system". Opt. Express. 19 (17): 15908–15918. Bibcode:2011OExpr..1915908S. doi:10.1364/OE.19.015908. PMID 21934954.
  22. ^ S. P. Groth; A.G. Polimeridis; J.K. White (2020). "Accelerating the discrete dipole approximation via circulant preconditioning". J. Quant. Spectrosc. Radiat. Transfer. 240: 106689. Bibcode:2020JQSRT.24006689G. doi:10.1016/j.jqsrt.2019.106689.
  23. ^ P. C. Chaumet; D. Sentenac; G. Maire; T. Zhang; A. Sentenac (2021). "IFDDA, an easy-to-use code for simulating the field scattered by 3D inhomogeneous objects in a stratified medium: tutorial". J. Opt. Soc. Am. A. 38 (12): 1841–1852. doi:10.1364/JOSAA.432685.
  24. ^ M. Shabaninezhad; M. G. Awan; G. Ramakrishna (2021). "MATLAB package for discrete dipole approximation by graphics processing unit: Fast Fourier Transform and Biconjugate Gradient". J. Quant. Spectrosc. Radiat. Transfer. 262: 107501. doi:10.1016/j.jqsrt.2020.107501.
  25. ^ B. M. Nebeker (1998). Modeling of light scattering from features above and below surfaces using the discrete-dipole approximation (PhD). Tempe, AZ, USA: Arizona State University.
  26. ^ E. Bae; H. Zhang; E. D. Hirleman (2008). "Application of the discrete dipole approximation for dipoles embedded in film". J. Opt. Soc. Am. A. 25 (7): 1728–1736. Bibcode:2008JOSAA..25.1728B. doi:10.1364/JOSAA.25.001728. PMID 18594631.
  27. ^ D. W. Mackowski (2002). "Discrete dipole moment method for calculation of the T matrix for nonspherical particles". J. Opt. Soc. Am. A. 19 (5): 881–893. Bibcode:2002JOSAA..19..881M. doi:10.1364/JOSAA.19.000881. PMID 11999964.
  28. ^ M. D. McMahon (2006). Effects of geometrical order on the linear and nonlinear optical properties of metal nanoparticles (PDF) (PhD). Nashville, TN, USA: Vanderbilt University.
  29. ^ V. L. Y. Loke; P. M. Mengüç; Timo A. Nieminen (2011). "Discrete dipole approximation with surface interaction: Computational toolbox for MATLAB". J. Quant. Spectrosc. Radiat. Transfer. 112 (11): 1711–1725. Bibcode:2011JQSRT.112.1711L. doi:10.1016/j.jqsrt.2011.03.012.
  30. ^ N. W. Bigelow; A. Vaschillo; V. Iberi; J. P. Camden; D. J. Masiello (2012). "Characterization of the electron- and photon-driven plasmonic excitations of metal nanorods". ACS Nano. 6 (8): 7497–7504. doi:10.1021/nn302980u. PMID 22849410.
  31. ^ N. Geuquet; L. Henrard (2010). "EELS and optical response of a noble metal nanoparticle in the frame of a discrete dipole approximation". Ultramicroscopy. 110 (8): 1075–1080. doi:10.1016/j.ultramic.2010.01.013.
  32. ^ S. Edalatpour; M. Čuma; T. Trueax; R. Backman; M. Francoeur (2015). "Convergence analysis of the thermal discrete dipole approximation". Phys. Rev. E. 91 (6): 063307. arXiv:1502.02186. Bibcode:2015PhRvE..91f3307E. doi:10.1103/PhysRevE.91.063307. PMID 26172822. S2CID 21556373.
  33. ^ S. A. Rosales; P. Albella; F. González; Y. Gutierrez; F. Moreno (2021). "CDDA: extension and analysis of the discrete dipole approximation for chiral systems". Opt. Express. 29 (19): 30020–30034. doi:10.1364/OE.434061.