모세관 압력

유체 정역학에서 모세관 압력(${\displaystyle p_{}}${\$displaystyle {p_{c$은 얇은 관에 있는 두 불규칙한 유체 사이의 압력이며(모세관 작용 참조) 관의 유체와 고체 벽 사이의 힘의 상호작용에서 비롯된다. 모세관 압력은 유체 수송의 반대나 추진력 둘 다의 역할을 할 수 있으며 연구와 산업 목적을 위한 중요한 특성이다(명칭 미세유체 설계 및 다공성 암석에서의 오일 추출). 자연현상에서도 관찰된다.

정의

모세관 압력은 다음과 같이 정의된다.

${\displaystyle p_{c}=p_{\text{non-texting phase}-p_{\text{texting phase}}}$

여기서:

${\displaystyle p_{}}$ ${\$은(는) 모세관 압력이다.

${\displaystyle p_{}}$ ${\displaystyle {\text{비파괴 단계}}_{}}$ ${\$}}은$($는) 비파괴 단계의 압력이다$$.

${\displaystyle p_{}}$ ${\displaystyle {\text{습식 단계}}_{}}$ ${\$}}은$($는) 습식 단계의 압력이다.

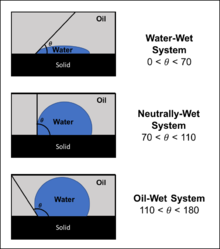
습식 단계는 비습식 단계 이전에 모세관 벽을 통해 우선적으로 확산되는 능력에 의해 확인된다. 유체의 "습도성"은 표면 장력, 가능한 최소의 공간을 차지하려는 유체의 경향을 움직이는 힘에 따라 달라지며 유체의 접촉 각도에 의해 결정된다.^[1] 유체의 "습도성"은 다양한 모세관 표면 특성(예: 거칠기, 친수성)에 의해 제어될 수 있다. 그러나 유수계통에서 물은 일반적으로 습윤단계인 반면 가스오일계통에서 기름은 일반적으로 침윤단계인 경우가 많다. 시스템에 관계 없이 두 유체 사이의 곡선 인터페이스에서 압력 차이가 발생한다.^[2]

방정식

모세관 압력 공식은 평형 상태에서 모세관 내의 두 유체 위상 사이의 압력 관계에서 도출된다. 즉, 위력 = 아래로 힘을 가하는 것이다. 이러한 힘은 다음과 같이 설명된다.^[1]

${\displaystyle {\text{force up = 모세관 주변을 따라 작용하는 유체의 인터페이스 장력}}$

${\displaystyle {\text{force down = (밀도 그라데이션 차이) x (횡단면적) x (관내 모세관 상승)}}}$

이러한 힘은 유체의 계면 장력과 접촉각, 모세관 반지름으로 설명할 수 있다. 흥미로운 현상, 모세관 상승(오른쪽 그림)은 이러한 특성이 모세관을 통해 흐르는 흐름을 유도하기 위해 어떻게 조합되는지, 그리고 이러한 성질을 시스템에서 어떻게 측정하는지 보여주는 좋은 예를 제공한다. 평형상태에서 두 유체의 힘을 상승시키고 하강시키는 관계를 설명하는 두 가지 일반적인 방정식이 있다.

Young-Laplace 방정식은 모세관 압력에 대한 힘 업 설명이며, 모세관 압력 방정식의 가장 일반적으로 사용되는 변동은 다음과 같다.^[2][1]

${\displaystyle p_{c}={\frac {2\frac \cs \cos \theta }{r_{c}}}}}}}$

여기서:

${\displaystyle \gamma }$ ${\displaystyle \gamma}$은(는) 인터페이스 장력임

${\displaystyle r}$ ${\displaystyle r}$은(는) 인터페이스의 유효 반지름임

${\displaystyle \theta }$ $[\displaystyle \theta }$은(는) 모세관 표면에 있는 액체의 습윤각이다.

모세관 압력에 대한 하중 감소 공식은 다음과 같다.^[1]

${\displaystyle p_{c}={\frac {\pi r^{2}h(\Gamma _{w}-\Gamma _{nw}}}{\pi r^{2}}}=h(\Gamma _{w}-\Gamma _{nw}})}$

여기서:

${\displaystyle h}$ $[\displaystyle h}$는 모세관 상승 높이임

${\displaystyle {\mathrm{\gamma }}_{}}$ ${\displaystyle w_{}}$ ${\$는 습식 단계의 밀도 경사로다.

${\displaystyle {\gamma n}_{}}$ ${\displaystyle w_{}}$ ${\$은(는) 비습기 단계의 밀도 경사로다.

적용들

미세유체학

미세유체학은 다양한 용도를 위한 다공성 물질이나 좁은 채널을 통한 소량의 유체 흐름의 제어 또는 운반에 대한 연구 및 설계다(예: 혼합, 분리 모세관 압력은 특정 공정을 최적화하기 위해 미세유체 장치에서 변경할 수 있는 많은 기하학적 관련 특성 중 하나이다. 예를 들어 모세관 압력이 증가하면 채널의 젖은 표면이 도관을 통해 액체를 끌어당긴다. 이것은 시스템에 펌프가 필요하지 않고 원하는 프로세스를 완전히 자율적으로 만들 수 있다. 모세관 압력은 또한 미세유체 장치의 유체 흐름을 차단하는 데 사용될 수 있다.

마이크로 채널의 모세관 압력은 다음과 같이 설명할 수 있다.

${\displaystyle p_{c}=-\displaysty\frac {cs\reft\fract_{b}+cos\tea_{t}}}}{d}}+{cos\cos\cos\{r}}}\right)}$

여기서:

${\$은(는) 액체의 표면 장력이다.

${\displaystyle {\theta }_{}}$ ${\displaystyle b_{}}$ ${\$은(는) 하단의 접점 각도임$$

${\displaystyle {\theta }_{}}$ ${\displaystyle t_{}}$ ${\$은(는) 상단의 접점 각도임$$

${\displaystyle {\theta }_{}}$ ${\displaystyle l_{}}$ ${\$은(는) 채널 왼쪽의 접점 각도임

${\displaystyle {\theta }_{}}$ ${\displaystyle r_{}}$ ${\$은(는) 채널 오른쪽의 접점 각도임

${\displaystyle d}$ ${\$는 깊이

${\displaystyle w}$ ${\$는 너비임

따라서 모세관 압력은 유체의 표면 장력, 유체의 접촉 각도 또는 기기 채널의 깊이와 폭을 변경하여 변경할 수 있다. 표면 장력을 바꾸기 위해 모세관 벽에 계면활성제를 바르면 된다. 접촉 각도는 기기 채널 내에서 갑작스러운 팽창 또는 수축에 의해 변화한다. 양의 모세관 압력은 유체 흐름의 밸브를 나타내고, 음의 압력은 유체가 마이크로 채널로 당겨지는 것을 나타낸다.^[3]

측정 방법

마이크로 유체학에서 정확한 압력 측정이 필요함에도 불구하고 마이크로 채널에서 모세관 압력을 물리적으로 측정하는 방법은 철저히 연구되지 않았다. 마이크로 유체 장치의 압력 측정과 관련된 일차적인 문제는 유체의 부피가 너무 작아서 표준 압력 측정 도구에 사용할 수 없다는 것이다. 몇몇 연구들은 크기를 바꾸는 압력 센서인 마이크로발롱의 사용을 제시했다. 혈압 측정에 역사적으로 사용되는 서보-눌링은 또한 LabVIEW 제어 시스템의 도움으로 미세 유체 채널에서 압력 정보를 제공하는 것으로 입증되었다. 본질적으로 마이크로피펫은 마이크로채널 유체에 담그고 유체 메니스크의 변화에 반응하도록 프로그램되어 있다. 마이크로피펫 내 유체의 변위는 전압 강하를 유도하여 펌프를 작동시켜 유체의 원래 위치를 복구한다. 펌프에 의해 가해지는 압력은 마이크로 채널 내의 압력으로 해석된다.^[4]

예

현재 미세유체학에 대한 연구는 관리 시점 진단 및 세포 분류 기법(실험실 온 어 칩 참조)을 개발하고 세포 행동(예: 세포 성장, 세포 노화)을 이해하는 데 초점을 맞추고 있다. 진단 분야에서 횡류 테스트는 모세관 힘을 이용해 다공성 막을 통한 유체 이송을 추진하는 공통 마이크로 유체 소자 플랫폼이다. 가장 유명한 가로 방향 유동 테스트는 양 또는 음의 신호를 나타내기 위해 포획선에 도달하면 체액이 처음에는 움푹 들어간 다음 다공성 막, 종종 셀룰로오스나 유리섬유를 통해 흐른다. 이 설계와 다른 몇몇 미세유체 장치의 장점은 단순성(예를 들어 작동 중 인간의 개입이 부족함)과 저비용이다. 단, 이러한 시험의 단점은 모세관 작용이 시작된 후 모세관 작용을 제어할 수 없기 때문에 시험 시간이 빨라지거나 느려질 수 없다는 것이다(유체 흐름 중에 특정 시간 의존적 공정이 일어나게 되면 문제가 될 수 있다).^[5]

모세관 압력 관련 설계 구성요소와 관련된 관리 시점 작업의 또 다른 예로는 다공성 막을 통한 여과에 의한 전혈에서 혈장 분리를 들 수 있다. 전혈에서 혈장을 효율적이고 대량으로 분리하는 것은 종종 HIV 바이러스 부하 테스트와 같은 전염병 진단을 위해 필요하다. 그러나 이 작업은 종종 임상 실험실 설정으로 제한되는 원심분리기를 통해 수행된다. 이 관리 시점 여과 장치의 예로는 패킹 베드 필터가 있는데, 이는 막 모공 내 비대칭 모세관 힘을 활용해 혈장과 전혈을 분리하는 능력을 입증했다.^[6]

석유화학공업

모세관 압력은 다공성 저장 암석 아래에서 지표면 이하의 탄화수소(석유나 천연가스 등)를 추출하는 데 중요한 역할을 한다. 이 측정은 저장고 유체 포화 및 캡 록 밀봉 용량을 예측하고 상대 투과성(제2의 불활성 유체가 있는 상태에서 운반되는 유체의 능력) 데이터를 평가하는 데 활용된다.^[7] 또한 다공성 암석의 모세관 압력은 저장 유체의 상상에 영향을 미치고, 따라서 추출 방법과 회복에 영향을 미치는 것으로 나타났다.^[8] 저수지 개발, 생산 및 관리(예: 탄화수소를 추출하는 것이 얼마나 쉬운지)를 위해서는 저수지 지질학적 특성을 이해하는 것이 중요하다.

Deepwater Horizon 기름 ^[dubious – discuss]유출은 석유화학 산업에 모세관 압력이 중요한 이유를 보여주는 사례다. 2010년 멕시코만에서 딥워터 호라이즌 석유 굴착기가 폭발하면서 최근 시행된 봉인을 뚫고 메탄가스가 굴착기 위와 밖으로 확장된 것으로 추정된다. 모세관 압력 연구(또는 모세관 압력 연구 부족)가 반드시 이 특정 기름 유출의 근원에 위치하지는 않지만, 모세관 압력 측정은 Deepwater Horizon 이벤트에서 이루어진 엔지니어링 결정에 영향을 줄 수 있는 저장소의 특성을 이해하는 데 중요한 정보를 제공한다.^[9]

모세관 압력은 석유 공학에서 볼 수 있듯이, 평형을 확립하기 위해 비습기 단계별로 습식 단계를 대체하는 데 필요한 압력으로 기록되는 실험실에서 모델링되는 경우가 많다.^[10] 참고로 공기와 브라인(석유화학 산업에서 중요한 시스템) 사이의 모세관 압력은 0.67 - 9.5 MPa로 나타났다.^[11] 석유 및 가스 산업에서 모세관 압력 관계를 예측, 측정 또는 계산하는 방법은 다양하다. 여기에는 다음이 포함된다.^[7]

레베렛 J 기능

Levelret J 기능은 모세관 압력과 모공 구조 사이의 관계를 제공하는 역할을 한다(Levelret J-기능 참조).

머큐리 주입

이 방법은 불규칙한 암석 표본(예를 들어 드릴 절단에서 발견된 표본)에 잘 적합하며 일반적으로 모세관 압력과 표본의 다공성 구조 사이의 관계를 이해하는 데 사용된다.^[12] 이 방법으로는 샘플록의 모공을 빼내고, 이어서 수은이 모공을 채워 압력을 증가시킨다. 한편, 각 주어진 압력의 수은 부피는 기록되어 모공 크기 분포로 주어지거나, 관련 오일/가스 데이터로 변환된다. 이 방법의 한 가지 함정은 유체-표면 상호작용을 설명하지 않는다는 것이다. 그러나 수은을 주입하고 데이터를 수집하는 전 과정이 다른 방법에 비해 빠르게 일어난다.^[7]

다공판법

다공성 플레이트 방법은 유체-공기 시스템의 모세관 압력 관계를 이해하는 정확한 방법이다. 이 과정에서 물을 채운 시료를 가스실 안에서도 물을 채운 평판 위에 놓는다. 가스는 압력을 증가시킬 때 주입되며, 따라서 판을 통해 물을 대체한다. 기체의 압력은 모세관 압력을 나타내며, 다공성 판에서 배출되는 물의 양은 표본의 수분 포화와 상관관계가 있다.^[7]

원심분리법

원심분리 방법은 모세관 압력과 중력 사이의 다음과 같은 관계에 의존한다.^[7]

${\displaystyle p_{c}=hg(\rho _{w}-\rho _{nw}})$

여기서:

${\displaystyle h}$ $[\displaystyle h}$는 모세관 상승 높이임

${\displaystyle g}$ $[\displaystyle g}$는 중력이다.

${\displaystyle {\rho }_{}}$ ${\displaystyle w_{}}$ ${\$는 습식 단계의 밀도임

${\displaystyle {\rho n}_{}}$ ${\displaystyle w_{}}$ ${\$는 비파괴$$ 단계의 밀도임

원심력은 본질적으로 작은 시험 플러그에 적용되는 모세관 압력으로 작용하며, 종종 브라인과 오일로 구성된다. 원심분리 과정에서 일정량의 브라인(brine)이 특정 회전 원심률로 플러그에서 배출된다. 유리병은 배출되는 유체의 양을 측정하는데, 이러한 측정치는 회전 속도와 배수량을 연관시키는 곡선을 만든다. 회전 속도는 다음 식에 의해 모세관 압력과 상관관계가 있다.

${\displaystyle p_{c}=7.9e^{-8}(\rho _{1}-\rho _{2}\omega ^{2}(r_{b}^{b}^{2}-r_{t}^{2})}$

여기서:

${\displaystyle r_{}}$ ${\displaystyle b_{}}$ ${\$는 코어 표본 하단의 회전 반지름이다.

${\displaystyle r_{}}$ ${\displaystyle t_{}}$ ${\$는 코어 표본 상단의 회전 반지름이다.

${\displaystyle \Omega }$ ${\displaystyle \omega}$이(가) 회전 속도임

이 방법의 주요 이점은 속도가 빠르고(몇 시간 내에 곡선을 생성하며) 특정 온도에서 수행되는 것에 제한되지 않는다는 것이다.^[13]

그 밖에 기압법, 중력평형법, 동적법, 반동적법, 과도법 등이 있다.

상관 관계

석유/천연가스 저장소의 모세관 압력을 모델링하기 위한 실험실 환경에서 모세관 압력을 측정하는 것 외에도 특정 암석 및 추출 조건을 설명하는 여러 관계가 있다. 예를 들어 R. H. Brooks와 A. T. Corey는 기체 침입을 경험하는 기름 포화 다공성 매체에서 오일을 배수하는 동안 모세관 압력에 대한 관계를 개발했다.^[14]

${\displaystyle p_{cgo}=p_{t}({\frac {1-S_{or}}{S_{or}}})^{{(1/\lambda )}}}}}}}}$

여기서:

${\displaystyle P_{}}$ ${\displaystyle c_{}}$ ${\displaystyle g_{}}$ ${\displaystyle o_{}}$ ${\$는 석유와 가스 단계 사이의 모세관 압력이다.

${\displaystyle S_{}}$ ${\displaystyle o_{}}$ ${\$는 오일 포화 상태임

${\displaystyle S_{}}$ ${\displaystyle o_{}}$ r ${\$는 모세관 압력이 높을 때 모공 속에 갇힌 채로 남아 있는 잔존유 포화상태다.

${\displaystyle P_{}}$ ${\displaystyle t_{}}$ ${\$는 임계값 압력(가스 위상이 흐를 수 있는 압력)이다$$.

${\displaystyle \lambda }$ ${\displaystyle \lambda }$은(는) 공극 크기 분포와 관련된 매개 변수임

> ${\displaystyle \lambda >2}$ 좁은 분포용

< ${\displaystyle \lambda <2}($넓은 분포의 경우

또한, R. G. Bentsen과 J. Anli는 기름기가 포화수를 대체하는 다공성 암석 표본에서 배수하는 동안 모세관 압력에 대한 상관관계를 개발하였다.^[15]

${\displaystyle p_{cow}=p_{t}-p_{cs}ln({\frac {S_{w}-S_{wi}}}}{1-S_{wi}}}}}}}}}$

여기서:

${\displaystyle P_{}}$ ${\displaystyle c_{}}$ ${\displaystyle o_{}}$ ${\displaystyle w_{}}$ ${\$은(는) 오일 단계와 물 단계 사이의 모세관 압력이다$$.

${\displaystyle P_{}}$ ${\displaystyle c_{}}$ ${\displaystyle s_{}}$ ${\$은 모세관 압력 함수의 모양을 제어하는 파라미터다$$.

${\displaystyle (S\frac{{}_{}{}_{}}{}}$ w ${\displaystyle \frac{w_{}}{}}$ ${\displaystyle \frac{{}_{}}{\mathrm{}}}$ 1${\displaystyle \frac{}{}}$- S ${\displaystyle \frac{w_{}}{}}$ i${\displaystyle \frac{{}_{}}{}}$) ${\displaystyle({\frac {S_{w}-S_{wi}}}}{1-S_{wi}}}}})$은 정규화된 습식 위상 포화이다.

${\displaystyle S_{}}$ ${\displaystyle w_{}}$ ${\$는 습식 단계의 포화도 입니다.

${\displaystyle S_{}}$ ${\displaystyle w_{}}$ ${\displaystyle i_{}}$ ${\$은(는) 수정 불가능한 습식 위상 포화이다.

모세관 평균치 대 수분 포화 곡선

저수지 시뮬레이터는 포화 높이 모델링 계산을 위해 1차 배수 모세관 압력 데이터를 사용하므로 1차 배수 모세관 압력 데이터는 포화도가 평균화되는 것과 동일한 방식으로 평균화되어야 한다. 또한 저장장치 시뮬레이터는 임비션 및 2차 배수 모세관 압력 데이터를 유체 변위 계산에 사용하므로 이러한 모세관 압력은 1차 배수 모세관 압력 데이터처럼 평균화해서는 안 된다. 이것들은 Levelret J-function에 의해 평균화될 수 있다. 평균 방정식은 다음과 같다.

일차 배수 모세관 압력과 정규화된 포화 데이터 평균 비교

${\displaystyle {\text{average Pc}}={\frac {\sum _{i=1}^{n}\left({\phi V_{\mathit {b}}P_{\mathit {c}}}\right)_{i}}{\sum _{i=1}^{n}\left({\phi V_{\mathit {b}}}\right)_{i}}}}$

여기서 $n{\displaystyle }$ ${\displaystyle n}$은 코어 표본의 수, $\varphi {\displaystyle }${\$displaystyle \phi$}은$$(는) 유효 다공성, ${\displaystyle V}$ b$${\$displaystyle Vb}$은 표본의 대량 볼륨, ${\displaystyle P}$ c ${\displaystytle Pc}$은 1차 배수 모필렬 압력 데이터 대 표준화된 수 포화수량이다.

평균 임비션 및 2차 배수 모세관 압력 대 정규화된 포화 데이터

${\displaystyle {\text{average Pc}}={\frac {\sum _{i=1}^{n}\left({\frac {P_{\mathit {c}}{\sqrt {k/\phi }}}{\gamma }}\right)_{i}}{\sum _{i=1}^{n}\left({\frac {\sqrt {k/\phi }}{\gamma }}\right)_{i}}}}$

여기서 $n{\displaystyle }$ ${\displaystyle n}$은(는) 코어 표본의 수, $\varphi {\displaystyle }$ ${\displaystyle \phi }$은(는) 유효 다공성, k ${\displaystyle k}$은(는) 절대 투과성, $\gamma {\displaystyle }$ ${\$$displaystyle$ $\gma}$은 인터페이스 장력 또는 IFT, $Pc {\$da$.$ta vs 정상화된 물 포화 상태

자연에서

니들 아이스

의료 및 에너지 적용을 위해 조작되는 것 외에도 모세관 압력은 다양한 자연현상의 원인이기도 하다. 예를 들어, 차가운 토양에서 볼 수 있는 바늘 얼음은 모세관 작용을 통해 발생한다. 바늘 얼음 연구에 대한 첫 번째 주요 공헌, 즉 간단히 말해서 서리 폭주 연구는 토양 얼음을 독자적으로 이해하려는 스티븐 태버(1929)와 군나르 베스코우(1935)가 했다. 태버의 초기 작업은 땅속 모공 크기가 서리 강하량에 어떤 영향을 미치는지 이해하는 것과 관련이 있었다. 그는 또한 서리 강하가 수정 성장에 유리하며 토양 수분 장력의 경사로 인해 물이 지표면 부근의 얼어붙은 전면을 향해 위로 상승한다는 것을 발견했다.^[17] 베스코우의 연구에서 그는 이 토양 수분 장력을 "모세압"(그리고 토양 물을 "모세수"로 정의했다. 베스코프는 토양 유형과 토양 입자에 대한 유효 응력이 서리 강도에 영향을 미친다고 판단했다. 여기서 효과적인 응력은 지상 압력과 모세관 압력의 합이다.^[18]

1961년, D.H. 에버렛은 얼음으로 채워진 모공 공간이 얼음 성장을 계속하는 이유를 이해하기 위해 태버와 베스코우의 연구를 상세히 설명했다. 그는 열역학적 평형 원리, 얼음 성장을 위한 피스톤 실린더 모델 및 다공성 매체에서의 물의 결빙을 이해하기 위해 다음과 같은 방정식을 활용했다(니들 얼음 형성에 직접 적용 가능).

${\displaystyle P_{s}-P_{l}=\PSI _{sl}{dA_{r}}}}}=\PSI _{dV}{\tilde{K}}}}}}$

여기서:

${\displaystyle P_{}}$ ${\displaystyle s_{}}$ ${\$은(는) 고체 결정의 압력이다.

${\displaystyle P_{}}$ ${\displaystyle l_{}}$ ${\$은(는) 주변 액체의 압력이다.

${\displaystyle {\mathrm{\psi }}_{}}$ ${\displaystyle s_{}}$ ${\displaystyle l_{}}$ ${\$은(는) 고체와 액체 사이의 인터페이스 장력이다.

${\displaystyle r_{}}$ ${\$은(는) 위상 경계의 표면 영역이다.

${\displaystyle V}$ ${\$는 크리스탈의 볼륨이다.

${\displaystyle \stackrel{}{K}}$~ ${\$은(는) 솔리드/액체 인터페이스의 평균 곡면성이다.

이 방정식과 모델을 가지고 에버렛은 고체-액체 인터페이스에서 다른 압력 조건이 주어진 물과 얼음의 행동에 주목했다. 에버렛은 얼음의 압력이 표면 아래의 액체의 압력과 같을 경우, 얼음의 성장이 모세관까지 계속될 수 없다고 판단했다. 따라서 추가적인 열 손실은 물이 모세관 위로 이동하여 상단 실린더에 동결하는 것이 가장 유리하다(바늘 얼음이 토양 표면 위에서 계속 자랄 때). 얼음의 압력이 증가함에 따라 고체와 액체 사이에 곡면 인터페이스가 생겨 얼음이 녹거나 평형이 다시 형성되어 더 많은 열 손실이 다시 얼음 형성으로 이어질 것이다. 전반적으로, 에버렛은 서리 덩어리(바늘 얼음의 발달에 대한 아날로그적)가 토양 속 모공 크기와 얼음과 물의 접점에 있는 에너지의 함수로 발생한다고 결정했다. 불행히도 에버렛의 모델의 단점은 표면에 미치는 토양 입자 영향을 고려하지 않았다는 것이다.^[19][20]

순환계

순환계의 모세혈관은 영양분을 공급하고 온몸에 노폐물을 배설하는 데 필수적이다. 모세혈관에는 모세혈관 수준에서 혈액 흐름을 제어하고 궁극적으로 모세혈관 교환 과정(예: 유체 흐름)에 영향을 미치는 (정수압 및 종양압력으로 인한) 압력 구배가 존재한다.^[21] 기술과 신체 구조의 한계로 인해 모세혈관 활동에 대한 대부분의 연구는 망막, 입술, 피부에서, 역사적으로 식인계나 서보 nulling 시스템을 통해 이루어진다. 모세혈관 내 모세혈관을 2D로 시각화하는 데 사용돼 왔으며, 사람의 모세혈관 압력은 평균 10.5~22.5mmHg, 제1형 당뇨·고혈압 환자의 압력 증가를 관찰한 것으로 보고됐다. 순환계통의 다른 구성 요소에 비해 모세관 압력은 낮지만 모세관 기능을 촉진하기에 충분하다.^[22]

참고 항목

• 모세관 작용
• 모세관수
• 분리압력
• 레베렛 J 기능
• 영-라플라스 방정식
• 라플라스 압력
• 표면장력
• 미세유체학
• 물_보전_곡선
• TEM 기능
• USBM 습윤성 지수

참조