공기질량(태양 에너지)

공기 질량 계수는 지구의 대기를 통과하는 직접 광학 경로 길이를 정의하는데, 이는 수직으로 위쪽으로 향하는 경로 길이에 상대적인 비율(즉, 정점에서)으로 표현된다. 공기 질량 계수는 태양 복사가 대기를 통과해 이동한 후 태양 스펙트럼의 특성을 파악하는 데 도움을 줄 수 있다.

공기질량계수는 표준화된 조건에서 태양전지의 성능을 특성화하기 위해 일반적으로 사용되며, 숫자 뒤에 나오는 구문 "AM"을 사용하는 경우가 많다. 'AM1.5'는 지상파 발전 패널 특성화 시 거의 보편적이다.

설명

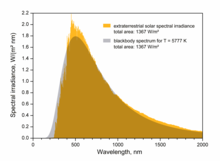
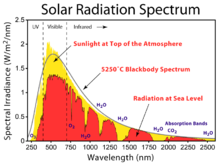
태양 복사열은 약 5800K의 검은색 차체 라디에이터와 밀접하게 일치한다.^[1] 그것이 대기를 통과할 때, 햇빛은 산란과 흡수에 의해 감쇠된다; 통과하는 대기가 많을수록 감쇠는 더 커진다.

햇빛이 대기를 통과하면서 화학 물질은 햇빛과 상호 작용하고 특정 파장을 흡수하여 지구 표면에 도달하는 단파장의 양을 변화시킨다. 이 과정의 보다 활동적인 요소는 수증기로서, 많은 파장에서 다양한 흡수 대역을 발생시키는 반면, 분자 질소, 산소, 이산화탄소는 이 과정을 더한다. 그것이 지구 표면에 도달할 때까지 스펙트럼은 극적외선과 자외선 사이에 강하게 제한된다.

대기 산란은 직사광선에서 더 높은 주파수를 제거하고 그것을 하늘에 흩뿌리는 역할을 한다.^[2] 이것이 하늘이 파란색으로 보이고 태양이 노란색으로 보이는 이유다. 즉, 고주파 청색 빛이 간접적으로 산란된 경로를 통해 관찰자에게 더 많이 도착하고, 푸른 빛이 직사 경로를 따라 덜 나타나 태양에 노란 색조를 주는 것이다.^[3] 태양 빛이 이동하는 대기의 거리가 클수록, 이러한 효과는 더 커지는데, 이는 태양이 대기를 통해 매우 비스듬히 이동할 때 새벽과 해질 무렵에 태양은 주황색 또는 빨갛게 보이는 이유 - 점진적으로 더 많은 블루스와 그린이 직사광선에서 제거되어 주황색 또는 적색으로 보인다. 태양에; 그리고 하늘은 분홍색으로 보인다. 왜냐하면 푸른색과 초록색이 너무 긴 길 위에 흩어져 있어서 관찰자에게 도착하기 전에 매우 약해지고, 그 결과 새벽과 해 질 무렵에 특징적인 분홍색 하늘이 생기기 때문이다.

정의

대기를 통과하는$$ 경로 길이 $L{\displaystyle }$ ${\displaystyle L}$과(와) 지구 표면에 대한 정규 분포를 기준으로$$ 한 $각도{\displaystyle }$z {\$displaystyle$ z$}$에서 발생하는 일사량의 경우, 공기량 ^[4]계수는 다음과 같다.

${\displaystyle AM={\frac {L}{L_{\mathrm{o}}}}}}}}}}$

(A.1)

여기서 $L{\displaystyle {}_{}}$ ${\displaystyle {o\mathrm{}}_{}}$ ${\$은 해수면에서 정점에서의 경로 길이(즉, 지구 표면과 정상)이다.

따라서 공기 질량 수는 하늘을 통과하는 태양의 표고 경로에 따라 달라지며, 따라서 하루의 시간과 일 년의 지나가는 계절에 따라, 그리고 관측자의 위도에 따라 달라진다.

계산

공기 질량에 대한 1차 근사치는 다음과 같다.

${\displaystyle AM\ 약 {\frac {1}{\cos \,z}\,}$

(A.1)

여기서 $z{\displaystyle }$ ${\displaystyle z}$는 도 단위의 절정각이다.

위와 같은 근사치는 대기의 유한한 높이를 간과하고, 수평선에서 무한한 공기량을 예측한다. 단, $z{\displaystyle }$ ${\displaystyle z}$ 값은 최대$$ 75°까지 합리적으로 정확하다. 수평선을 향한 경로 두께를 보다 정확하게 모델링하기 위해 Kasten과 Young(1989)이 제안한 것과 같은 많은 개선사항이 제안되었다.^[5]

${\displaystyle AM={\frac {1}{\cos \,z+0.50572\,(96.07995-z)^{-1.6364}},}$

(A.2)

이러한 모델의 보다 포괄적인 목록은 다양한 대기 모델 및 실험 데이터 세트에 대한 주요 기사인 에어매스에 수록되어 있다. 해수면에서 수평선 방향으로 공기 질량(${\displaystyle }$ ${\displaystyle z}$ $$= 90°) 대략 38살이다.^[6]

대기를 단순한 구형 쉘로 모델링하면 합리적인 근사치를 제공한다.^[7]

${\displaystyle AM={\sqrt {(r\cos z)^{2}+2r+1}\;-\;r\cos z\,}$

(A.3)

where the radius of the Earth ${\displaystyle R_{\mathrm {E} }}$ = 6371 km, the effective height of the atmosphere ${\displaystyle y_{\mathrm {atm} }}$ ≈ 9 km, and their ratio ${\displaystyle r=R_{\mathrm {E} }/y_{\mathrm {atm} }}$ ≈ 708.

이러한 모델은 아래 표에서 비교된다.

해수면에서의 공기 질량 계수 추정

$(\displaystyle z}$	플랫 어스	카스텐 & 영	구면 껍질
정도	(A.1)	(A.2)	(A.3)
0°	1.0	1.0	1.0
60°	2.0	2.0	2.0
70°	2.9	2.9	2.9
75°	3.9	3.8	3.8
80°	5.8	5.6	5.6
85°	11.5	10.3	10.6
88°	28.7	19.4	20.3
90°	$\displaystyle \infit }$	37.9	37.6

이는 이러한 목적을 위해 대기가 효과적으로 하단 9km 부근으로 집중되는 것으로 간주될 수 있음을 시사한다.^[8] 즉, 기본적으로 모든 대기 영향은 대류권 하단의 대기 질량에 기인한다. 이것은 태양 강도에 미치는 대기 영향을 고려할 때 유용하고 간단한 모델이다.

경우들

• AM0

5,800 K 검정색 몸체에 의해 대략적으로 추산되는 대기 밖의 스펙트럼을 "AM0"이라고 하는데, 이는 "대기 0"을 의미한다. 통신 위성의 태양 전지처럼 우주 전력 응용에 사용되는 태양 전지는 일반적으로 AM0을 사용하는 것이 특징이다.

• AM1

태양이 직접 머리 위에 있는 대기를 통과해 해수면으로 이동한 후의 스펙트럼을 정의하면 "AM1"이라고 한다. 이것은 "하나의 분위기"를 의미한다. AM1(${\displaystyle }$ ${\displaystyle z}$=0°) AM1.1에 연결(${\displaystyle }$ ${\displaystyle z}$=25°) 적도 및 열대 지역의 태양 전지 성능을 추정하는 데 유용한 범위다.

• AM1.5

태양 전지판은 일반적으로 정확히 한 대기의 두께에서 작동하지 않는다. 태양이 지구 표면과 각도를 이루면 유효 두께가 더 커질 것이다. 유럽, 중국, 일본, 미국 및 그 밖의 지역(인도 북부, 남아프리카, 오스트레일리아 포함)을 가로지르는 세계의 주요 인구 중심지, 그리고 태양열 설치 및 산업은 온대지방에 있다. 따라서 중간 위도에서 스펙트럼을 나타내는 AM 번호는 훨씬 더 일반적이다.

"AM1.5"는 1.5기압 두께로 $z{\displaystyle }${\디스플레이 스타일 $z}$=$48$.2°의 태양 정점 각도에 해당한다. 한낮의 중위도의 여름철 AM 숫자는 1.5 미만인 반면, 더 높은 수치는 아침과 저녁, 그리고 일년 중 다른 시간에 적용된다. 따라서 AM1.5는 중위도의 전체 연간 평균을 나타내는 데 유용하다. 1.5의 구체적인 값은 1970년대에 표준화를 목적으로 선택되었으며, 이는 미국의 태양 복사 강도 데이터의 분석에 기초한다.^[9] 이후 태양광 산업은 집광시스템에 사용되는 것을 포함해 지상 태양전지나 모듈의 모든 표준화된 시험이나 정격에 AM1.5를 사용하고 있다. 태양광 발전 애플리케이션과 관련된 최신 AM1.5 표준은 ASTM G-173^[10][11] 및 IEC 60904이며, 모두 SMARTS 코드로 얻은 시뮬레이션에서 도출되었다.

A.M.1.5에 따른 일광(이 버전)의 조도는 109,870룩스(A.M. 1.5 스펙트럼과 1000.4 W/m에² 대응)로 주어진다.

• AM2-3

AM2(${\displaystyle }$ ${\displaystyle z}$=60°) AM3에 연결(${\displaystyle }$ ${\displaystyle z}$=70°) 북유럽과 같이 높은 위도에 설치된 태양 전지의 전체 평균 성능을 추정하는 데 유용한 범위다. 이와 유사하게 AM2에서 AM3는 온대 위도에서 겨울 시간 성능을 추정하는데 유용하다. 예를 들어, 37°의 낮은 위도에서 겨울철에 공기량 계수가 하루의 모든 시간에 2보다 크다.

• AM38

AM38은 일반적으로 수평 방향의 기단(${\displaystyle }$ ${\displaystyle$ z$}$=$90$°)으로 간주된다. 해발에서^[6] 그러나 실제로 다음 절의 태양 강도에서 설명한 대로 수평선에 가까운 각도에서 받는 태양 강도의 변동성이 높다.

• 높은 고도에서

상대적 공기 질량은 태양의 정점 각도의 함수일 뿐, 따라서 국부 상승에 따라 변하지 않는다. 반대로, 상대적 공기량에 국부 대기압을 곱하고 표준(해수위) 압력으로 나눈 것과 같은 절대 공기량은 해수면 위로 상승하면서 감소한다. 예를 들어, 알티플라노 지역에서와 같이 높은 고도에 설치된 태양전지 판넬의 경우, 해수면에서의 해당 위도보다 낮은 절대 AM 번호, 즉 적도를 향해 1 미만인 AM 번호, 그리고 그에 상응하여 다른 위도의 경우 위에 열거한 수보다 낮은 절대 AM 번호를 사용할 수 있다. 그러나 이 접근방식은 대략적이며 권장되지 않는다. 상대적 공기 질량(예: 1.5)과 정밀 조사 대상 부지의 특정 고도에서의 실제 대기 조건에 기초하여 실제 스펙트럼을 시뮬레이션하는 것이 가장 좋다.

태양 강도

집열기의 태양 강도는 공기 질량 계수가 증가함에 따라 감소하지만, 단순하거나 선형적인 방식이 아닌 복잡하고 가변적인 대기 요인 때문에 감소한다. 예를 들어, 거의 모든 고에너지 방사선이 상층 대기(AM0과 AM1)에서 제거되므로 AM2는 AM1보다 2배 이상 나쁘지는 않다. 더욱이 수증기, 에어로졸, 광화학 스모그와 같은 대기 감쇠에 기여하는 많은 요소에서 큰 변동성이 있다.^[12] 대기 오염 수준에 따라 전체적인 감쇠는 수평선을 향해 최대 ±70%까지 변화할 수 있으며, 특히 대기의 낮은 층의 영향이 여러 가지로 증폭되는 수평선을 향한 성능에 큰 영향을 미친다.

태양 강도 대 기단에 대한 하나의 근사 모델은 다음과 같다.^[13][14]

${\displaystyle I=1.1\time I_{\mathrm {o}}\time 0.7^{(AM^{0.678})\,},}$

(I.1)

여기서 지구의 대기 $I{\displaystyle {}_{}}$ ${\displaystyle {o\mathrm{}}_{}}$ ${\$1.353 kW/m의² 외부 태양 강도 및 1.1의 인수는 확산 성분이 직접 성분의 10%라고 가정하여 도출된다.^[13]

이 공식은 예상 공해 기반 변동성의 중간 범위 내에 편안하게 들어맞는다.

태양 강도 대 절정각 $z{\displaystyle }$ ${\displaystyle z}$ 및$$ 공기 질량 계수 AM

$(\displaystyle z}$	AM	공해로[12] 인한 범위	공식(I.1)	ASTM G-173[11]
정도		W/m2	W/m2	W/m2
-	0	1367[15]	1353	1347.9[16]
0°	1	840 .. 1130 = 990 ± 15%	1040
23°	1.09	800 .. 1110 = 960 ± 16%[17]	1020
30°	1.15	780 .. 1100 = 940 ± 17%	1010
45°	1.41	710 .. 1060 = 880 ± 20%[17]	950
48.2°	1.5	680 .. 1050 = 870 ± 21%[17]	930	1000.4[18]
60°	2	560 .. 970 = 770 ± 27%	840
70°	2.9	430 .. 880 = 650 ± 34%[17]	710
75°	3.8	330 .. 800 = 560 ± 41%[17]	620
80°	5.6	200 .. 660 = 430 ± 53%	470
85°	10	85 .. 480 = 280 ± 70%	270
90°	38		20

이는 지평선 위 몇 도에서만 상당한 전력을 이용할 수 있음을 보여준다. 예를 들어 태양이 수평선 위로 약 60° 이상일 때(${\displaystyle }$ ${\displaystyle$ z$}<$30°) 태양 강도는 약 1000 W/m이다²(위 표에 나온 것처럼 등식 I.1로부터). 반면 태양이 수평선 위로 15°만 있을 때(${\displaystyle }$ ${\displaystyle z}$ $$=75°). 태양 강도는 여전히 최대 수위의 약 600W/m² 또는 60%이다; 수평선 위 5°에서만 여전히 최대 수치의 27%이다.

높은 고도에서

해발 수 킬로미터까지 정확하고 고도에 따라 강도가 증가하기 위한 한 가지 대략적인 모델은 다음과 같다.^[13][19]

${\displaystyle I=1.1\time I_{\mathrm {o}}\time [(1-h/7.1)0.7^{0.678}}+h/7.1]\,}$

(I.2)

여기서 $h{\displaystyle }$ ${\displaystyle h}$은(는) 해발 고도(km)의$$ 태양열 집열기 높이이고 $A{\displaystyle }$ ${\displaystyle M}$ ${\displaystyle AM}$은 해발 고도(A.2부터)에 집열기가 설치된 것처럼 공기 질량(A.2부터)이다$$.

또는 관련된 유의한 실제 가변성을 고려할 때, 동질 구형 모델을 AM 추정에 적용할 수 있다.

${\displaystyle AM={\sqrt {(r+c)^{2}\cos ^{2}z+(2r+1+c)(1-c)}}\;-\;(r+c)\cos z\,}$

(A.4)

여기서 대기 및 수집기의 정규화된 높이는 $각각{\displaystyle }$ r${\displaystyle }$= ${\displaystyle {R\mathrm{}}_{}}$ ${\displaystyle {}_{}}$/ y ${\displaystyle a{}_{}}$ ${\displaystyle {\mathrm{t}}_{}}$ m ${\$ ≈$$ 708(위의 경우) $및{\displaystyle }$ c${\displaystyle }$= ${\displaystyle h}$ /${\displaystyle y{}_{}}$ ${\displaystyle {a\mathrm{}}_{}}$ ${\displaystyle {\mathrm{t}}_{}}$ ${\$

그런 다음 위의 표 또는 적절한 방정식(각각 평균, 오염 또는 깨끗한 공기의 I.1 또는 I.3 또는 I.4)을 사용하여 AM의 강도를 일반적인 방법으로 추정할 수 있다.

I.2와 A.4의 이러한 근사치는 각각 약 6km와 9km의 AM0 성능 수준으로 감소하는 것을 암시하는 해발 수 킬로미터의 고도에만 사용하기에 적합하다. 이와는 대조적으로 높은 에너지 구성 요소의 감쇠의 많은 부분은 오존층 - 약 30 km 고도에서 발생한다.^[20] 따라서 이러한 근사치는 지상 수집기의 성능을 추정하는 데만 적합하다.

태양전지 효율

실리콘 태양 전지는 대기 중에 손실된 스펙트럼의 부분에 그다지 민감하지 않다. 지구 표면에서 발생하는 스펙트럼은 실리콘의 밴드갭과 더 밀접하게 일치하기 때문에 실리콘 태양 전지는 AM0보다 AM1에서 더 효율적이다. 이러한 직관에 반하는 결과는 단순히 실리콘 셀이 대기가 걸러내는 고에너지 방사선을 별로 활용할 수 없기 때문에 발생한다. 아래 그림과 같이 AM0에서 효율이 낮더라도 일반 태양전지의 총 출력전력(P_out)은 AM0에서 여전히 가장 높다. 반대로 스펙트럼의 형상은 대기두께가 더 증가해도 크게 변하지 않고, 따라서 1 이상의 AM 숫자에 대해서는 셀 효율이 크게 변하지 않는다.

출력 전력 대 공기량 계수

AM	태양 강도	출력 전력	효율성
	Pin W/m2	Pout W/m2	Pout / Pin
0	1350	160	12%
1	1000	150	15%
2	800	120	15%

이는 태양에너지가 "무료"이며 가용 공간이 제한이 아닌 경우 총 P_out, P와_out 같은 다른 요소들이 효율성(P_out/P_in)보다 더 중요한 고려사항인 경우가 많다는 일반적인 점을 보여준다.

참고 항목

참고 및 참조