위그너 분포 함수

이 글에는 여러 가지 문제가 있다.이 문제를 개선하거나 대화 페이지에서 토의하십시오.(이러한 템플릿 메시지를 제거하는 방법 및 시기 알아보기) 이 글은 일반적인 참고문헌 목록을 포함하고 있지만, 그에 상응하는 인라인 인용구가 충분하지 않다. 좀 더 정밀한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오.(2015년 11월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기) 이 기사는 위키피디아의 품질 기준을 충족시키기 위해 정리가 필요할 수 있다.특정한 문제는 수학이 이미지로 저장된다는 것이다. 가능한 경우 이 문서를 개선하는 데 도움을 주십시오. (2017년 11월) (이 템플리트 메시지를 제거하는 방법과 시기 알아보기) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

WDF(Wigner distribution function)는 신호 처리에 시간 빈도 분석의 변환으로 사용된다.

WDF는 1932년 유진 위그너에 의해 고전적 통계역학에 대한 양자보정을 설명하기 위해 물리학에서 처음 제안되었으며, 위상공간에서 양자역학에서 중요한 역할을 한다(비교에 의해, 다음을 참조).위그너 준확률 분포, 위그너 함수 또는 위그너-빌 분포라고도 한다.

위치-모멘텀과 시간-주파수 결합 쌍 사이의 공유 대수 구조를 고려할 때, 이 글의 주제인 시간-주파수 분석의 변환으로서 신호 처리에도 유용하게 사용된다.가보르 변환과 같은 짧은 시간 푸리에 변환에 비해 위그너 분포 함수는 불확실성 원리의 한계 내에서 수학적으로 가능한 가장 높은 시간 대 주파수 분해능을 제공한다.단점은 신호 성분의 각 쌍과 양수 및 음수 주파수 사이에 큰 교차 항이 도입되어 함수의 원래 제형이 대부분의 분석 애플리케이션에 적합하지 않다는 것이다.위그너 분포 함수의 선명성은 보존하되 교차 용어는 대부분 억제하는 후속 수정이 제안되었다.

수학적 정의

위그너 분포 함수에 대한 정의는 여러 가지가 있다.여기에 제시된 정의는 시간 빈도 분석에만 한정된다.시계열 $x{\displaystyle }$[ ${\displaystyle t}$ ${\displaystyle ]}$ ${\displaystyle x[t]}$을(를) 고려할 때$,$ 이 시계열의 비스테이션 자기 상관 함수는

${\displaystyle C_{x}(t_{1},t_{2})=\좌측\langle \left(x[t_{1}]-\mu[t_{1}]\우측)\좌측(x[t_{2}]-\mu[t_{2}]-\우측)^{*}\right\angle ,}$

여기서 $⟨{\displaystyle }$ ${\displaystyle \cdots }$ ${\displaystyle ⟩}$ ${\displaystyle \langle \cdots \rangle }$은 프로세스의 가능한 모든 실현에 대한 평균을 나타내며$$ $\mu {\displaystyle }$( ${\displaystyle t}$) ${\displaystyle \mu (t)}$은 시간의 함수가 될 수도 있고 아닐 수도 있는 평균이다.The Wigner function ${\displaystyle W_{x}(t,f)}$ is then given by first expressing the autocorrelation function in terms of the average time ${\displaystyle t=(t_{1}+t_{2})/2}$ and time lag ${\displaystyle \tau =t_{1}-t_{2}}$, and then Fourier transforming th뒤떨어지다

${\displaystyle W_{x}(t,f)=\int _{-\nothy }^{-}{\c_{x}\flt(t+{\frac{\}}{{2}}, t-{\pi itau }\dau}.$

그래서 단일 (평균 영점) 시계열의 경우 위그너 함수는 간단히 다음에 의해 주어진다.

${\displaystyle W_{x}(t,f)=\int _{-\infty }^{\infty }x\left(t+{\frac {\tau }{2}}\right)\,x^{*}\left(t-{\frac {\tau }{2}}\right)\,e^{-2\pi i\tau f}\,d\tau .}$

위그너 함수의 동기는 정지 공정의 경우$$ 항상 $t{\displaystyle }$ ${\displaystyle t}$ 스펙트럼 밀도 함수로 감소하지만, 비정전 자기 상관 함수와 완전히 동등하다는 것이다.따라서 위그너 함수는 스펙트럼 밀도가 시간에 따라 어떻게 변화하는지 (거의) 알려준다.

시간 빈도 분석 예제

여기 WDF가 시간 빈도 분석에서 어떻게 사용되는지를 보여주는 몇 가지 예가 있다.

상수 입력 신호

입력 신호가 일정할 때, 그 시간 주파수 분포는 시간 축을 따라 수평선이 된다.예를 들어, x(t)가 1이면

${\displaystyle W_{x}(t,f)=\int _{-\infit }^{-i2\pi \tau \,f}\,d\tau =\delta (f)}$

사인파 입력 신호

입력 신호가 정현상 함수인 경우, 그 시간 주파수 분포는 정현상 신호의 주파수에 의해 시간 축과 평행한 수평선이다.예를 들어, x(t) = e인 경우,

${\displaystyle {\reasoned}W_{x}(t,f)&=\int _{-\infty }^{\infty }e^{i2\pi k\left(t+{\frac {\tau }{2}}\right)}e^{-i2\pi k\left(t-{\frac {\tau }{2}}\right)}e^{-i2\pi \tau \,f}\,d\tau \\&=\int _{-\infty }^{\infty }e^{-i2\pi \tau \left(f-k\right)}\,d\tau \\&=\delta (f-k).\end{정렬}}}$

처프 입력 신호

입력 신호가 선형 처프 함수일 때, 순간 주파수는 선형 함수다.이는 시간 주파수 분포가 직선이어야 한다는 것을 의미한다.예를 들어, 다음과 같다.

${\displaystyle x}$( ${\displaystyle t}$)${\displaystyle }$= e ${\displaystyle {}^{}}$ ${\displaystyle 2^{}}$ ${\displaystyle {\mathrm{\pi k}}^{}}$ ${\displaystyle {{}^{}}^{}}$ ${\displaystyle {{2\mathrm{}}^{}}^{}}$ ${\$

그 순간 주파수는

${\displaystyle {\frac {1}{2\pi }{d(2\pi kt^{2}){dt}=2kt~,}$

그리고 그것의 WDF

${\displaystyle {\reasoned}W_{x}(t,f)&=\int _{-\infty }^{\infty }e^{i2\pi k\left(t+{\frac {\tau }{2}}\right)^{2}}e^{-i2\pi k\left(t-{\frac {\tau }{2}}\right)^{2}}e^{-i2\pi \tau \,f}\,d\tau \\&=\int _{-\infty }^{\infty }e^{i4\pi kt\tau }e^{-i2\pi \tau f}\,d\tau \\&=\int _{-\infty }^{\infty }e^{-i2\pi \tau (f-2kt)}\,d\tau \\&=\delta (f-2kt)~.\end{정렬}}}$

델타 입력 신호

입력 신호가 델타 함수인 경우, 입력 신호는 t=0에서 0이 아닐 뿐이고 무한 주파수 성분을 포함하므로, 그 시간 주파수 분포는 원점을 가로지르는 수직선이어야 한다.이것은 델타 함수의 시간 주파수 분포도 델타 함수가 되어야 한다는 것을 의미한다.WDF별

${\displaystyle {\reasoned}W_{x}(t,f)&=\int _{-\infty }^{\infty }\delta \left(t+{\frac {\tau }{2}}\right)\delta \left(t-{\frac {\tau }{2}}\right)e^{-i2\pi \tau \,f}\,d\tau \\&=4\int _{-\infty }^{\infty }\delta (2t+\tau )\delta (2t-\tau )e^{-i2\pi \tau f}\,d\tau \\&=4\delta (4t)e^{i4\pi tf}\\&=\delta (t)e^{i4\pi tf}\\&=\delta (t).\end{정렬}}}$

위그너 분배 기능은 입력 신호의 위상이 2차 이하일 때 시간 주파수 분석에 가장 적합하다.그러한 신호에 대해 WDF는 입력 신호의 시간 주파수 분포를 정확하게 생성할 수 있다.

박스카 함수

( )={ t < / 에는 $displaystyle x(t)={\displaystyle{case}$1& $t <1/2\\\\\0\{\text}}}\case}\end{case}}}},$

직사각형 함수 ⇒

${\displaystyle W_{x}(t,f)={\begin{case}{\frac {1}{\pi f}}\sin(2\pi f\{1-2t \}}&t <1/2\\0\{\mbox{otherwise}}}}}\case}}}}}}}}}}}}}}}}}}}}}}}}}}}}}"$

교차기 속성

위그너 분포 함수는 선형 변환이 아니다.교차 용어("시간 박동")는 입력 신호에 둘 이상의 성분이 있을 때 발생하며, 주파수 박동에 시간적으로 유사하다.^[1]조상 물리학 위그너 준확률 분포에서 이 용어는 충실한 기대치에 필요한 중요하고 유용한 물리학 결과를 가지고 있다.이와는 대조적으로, 단시간 푸리에 변환은 이 기능을 가지고 있지 않다.WDF의 부정적인 특징은 고전적 신호의 가보르 한계를 반영하며, 양자 구조의 가능한 언더레이와 물리적으로 관련이 없다.

다음은 위그너 분포 함수의 교차기 특징을 보여주는 몇 가지 예들이다.

• ${\displaystyle x(t)={\case}\cos(2\pi t)&t\leq -2\\\cos(4\pi t)&-2<t\cos(3\pi t)&gt;2\cos(3\pi t)&gt;2\end{case}}}}}}$
• ${\displaystyle x(t)=e^{it^{3}}$

교차기 난이도를 줄이기 위해 문헌에서 몇 가지 접근법이 제안되어 왔으며,^[2][3][4] 그 중 일부는 수정된 위그너 분포함수, 가보르-위그너 변환, 최윌리엄스 분포함수, 코헨의 계급 분포로서 새로운 변혁으로 이어진다.

위그너 분포 함수의 속성

위그너 분포 함수는 다음 표에 나열된 몇 가지 명백한 속성을 가지고 있다.

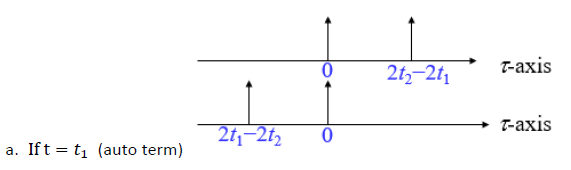
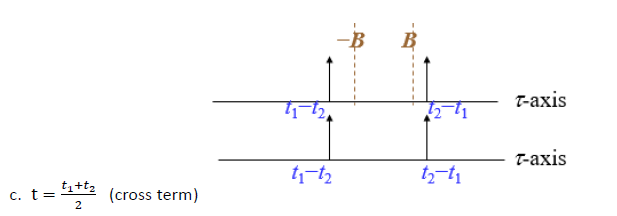
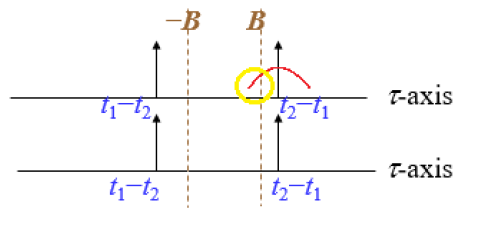
투영 속성

${\displaystyle {\begin{aligned} x(t) ^{2}&=\int _{-\infty }^{\infty }W_{x}(t,f)\,df\\ X(f) ^{2}&=\int _{-\infty }^{\infty }W_{x}(t,f)\,dt\end{aligned}}}$

에너지 특성

${\displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }W_{x}(t,f)\,df\,dt=\int _{-\infty }^{\infty } x(t) ^{2}\,dt=\int _{-\infty }^{\infty } X(f) ^{2}\,df}$

복구 속성

${\displaystyle {\begin{aligned}\int _{-\infty }^{\infty }W_{x}\left({\frac {t}{2}},f\right)e^{i2\pi ft}\,df&=x(t)x^{*}(0)\\\int _{-\infty }^{\infty }W_{x}\left(t,{\frac {f}{2}}\right)e^{i2\pi ft}\,dt&=X(f)X^{*}(0)\end{aligned}}}$

평균 조건 빈도 및 평균 조건 시간

${\displaystyle {\begin{aligned}X(f)&= X(f) e^{i2\pi \psi (f)},\quad x(t)= x(t) e^{i2\pi \phi (t)},\\{\text{if }}\phi '(t)&= x(t) ^{-2}\int _{-\infty }^{\infty }fW_{x}(t,f)\,df\\{\text{ and }}-\psi '(f)&= X(f) ^{-2}\int _{-\infty }^{\infty }tW_{x}(t,f)\,dt\end{aligned}}}$

모멘트 특성

${\displaystyle {\classed}\int _{-\infit }^{\int _{-\infit }^{\infit }^{\n}W_{x}(t,f)\,dt\,df&=\int _{-\infty }^{\infty }t^{n} x(t) ^{2}\,dt\\\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f^{n}W_{x}(t,f)\,dt\,df&=\int _{-\infty }^{\infty }f^{n} X(f) ^{2}\,df\end{aligned}}}$

실재질

${\displaystyle W_{x}^{*}(t,f)=W_{x}(t,f)}$

영역 속성

${\displaystyle {\reasoned}{\text}}}x(t)&=0{\text{{}t_{0}{\text{{}}{{}text{}}{{}w_{x}(t,f)=0{}text{{}}}}{{\text{}}}}}}{\text{{}}}text{}}}}}}}}}text{{{{{}}}}}text}}}}}}}}}}x(t)&=0{\text{{t_{0}{\text{{}{\text{{}}}{{w_{x}(t,f)=0{text{}}}}}의 경우:{t.{0}\ended}}}}}}}}$

곱셈 정리

${\displaystyle {\reasoned}{\text}}}y(t)&=x(t)h(t)\{\text{\data.}{{y}(t,f)&=\int _{-\infit }^{-\\nothy }{w_{x}(t, f-\rho ),d\rho \ended}}}}}}}}}}}.$

콘볼루션 정리

${\displaystyle {\reasoned}{\text}}}y(t)&=\int _{-\int _{-\infit }^{}x(t-\tau )h(\tau )\,d\tau \\\{\text}}{}W_{y}(t,f)&=int _{-\inf}{{{w_{x},rhof.W_{h}(t-\rho ,f)\,d\rho \end{aigned}}}$

상관 정리

${\displaystyle {\reasoned}{\text}}}y(t)&=\int _{-\int _{-\nft }^{\nft }x(t+\tau )h^{*(\tau )\,d\tau{\text{}}\}\}\\\\W_{y}(t,\omega )&=\int _{-\infit }^{\\note }W_{x}(\rho ,\omega )W_{h}(-t+\rho ,\omega )\,d\rho \end{aigned}}}$

시간 변화 공분산

${\displaystyle {\reasoned}{\text}}}y(t)&=x(t-t_{0})\\\text{{\text}{{}}{{W_{f)&=W_{x}(t-t_{0}f)\ended}}}}}}}$

변조 공분산

${\displaystyle {\reasoned}{\text}}}y(t)&=e^{i2\pi f_{0}t(t)\\{0}x(t)\\\text{}{{}w_{x}(t,f_{0})\end{aigned}}}}}}}인 경우$

척도 공분산

${\displaystyle {\reasoned}{\text}}}y(t)&={\sqrt{a}x(at){\text{}}{{}a}}}{{\text{}{\text{}} 그 다음 }W_{y}(t,f)&=W_{frac{a}}\end{a}}}}}}}}}}}}}}$

윈도우 위그너 분배 기능

신호가 시간제한이 아닐 때는 위그너 분배기능을 구현하기 어렵다.따라서 우리는 그 통합 부분에 새로운 기능(마스크)을 추가해서, 음의 무한대에서 양의 무한대로의 모든 길을 통합하는 대신에 원래의 기능의 일부만 구현하면 된다.Original function: ${\displaystyle W_{x}(t,f)=\int _{-\infty }^{\infty }x\left(t+{\frac {\tau }{2}}\right)\cdot x^{*}\left(t-{\frac {\tau }{2}}\right)e^{-j2\pi \tau f}\cdot d\tau }$ Function with mask: ${\displaystyle W_x(t,f)={\int }_{}^{}}$${\displaystyle W_{x}(t,f)=\int _{-\infty }^{\infty }w(\tau )x\left(t+{\frac {\tau }{2}}\right)\cdot x^{*}\left(t-{\frac {\tau }{2}}\right)e^{-j2\pi \tau f}\cdot d\tau }$ ${\displaystyle w(\tau )}$ is real and time-limited

실행

정의에 따라:

${\displaystyle {\reasoned}W_{x}(t,f)=\int _{-\infty }^{\infty }w(\tau )x\left(t+{\frac {\tau }{2}}\right)\cdot x^{*}\left(t-{\frac {\tau }{2}}\right)e^{-j2\pi \tau f}\cdot d\tau \\W_{x}(t,f)=2\int _{-\infty }^{\infty }w(2\tau ')x\left(t+\tau '\right)\cdot x^{*}\left(t-\tau '\right)e^{-j4\pi \tau 'f}\cdot d\tau '\\W_{x}(n\Delta _{t},m\Delta _{f}=2\sum _{p=-\ft }^{p=\ft }w(2p\Delta _{t}x(n+p)\델타 _{t}x^{\ast }(n-p)\델타 _{t}e^{-j4\pi mp\Delta _{t}\Delta _{f}\Delta _{t}\ended}}}}}$

> → ( )의$$ 경우 ${\displaystyle \mathrm{w}}$(${\displaystyle }$t${\displaystyle }$) = ${\$$displaystyle$ $w(t)=$$0$ = <- Q ${\displaystyle t$$>B\rightarrow w (2p\Delta$ $_$${$$})$ = 0이라고 가정합시다$.$

${\displaystyle {\reasoned}W_{x}(n\Delta _{t},m\Delta _{f}=2\sum _{p=-Q}^{Q}w(2p\Delta _{t}x(n+p)\델타 _{t}x^{\ast }(n-p)\델타 _{t}e^{-j4\pi mp\Delta _{t}\Delta _{f}\Delta _{t}\ended}}}}}$

$x{\displaystyle }$( ${\displaystyle t}$)${\displaystyle }$= ${\displaystyle \Delta }$( ${\displaystyle t}$- ${\displaystyle {t\mathrm{}}_{}}$ ${\displaystyle {}_{}}$)${\displaystyle }$+ ${\displaystyle \Delta }$( t${\displaystyle }$- ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$) ${\displaystyle$ x$(t)=\delta (t-t_{1}}+\delta (t-t_{2})$를 예로$$ 들어보자.

${\displaystyle {\reasoned}W_{x}(t,f)=\int _{-\infty }^{\infty }w(\tau )x\left(t+{\frac {\tau }{2}}\right)\cdot x^{*}\left(t-{\frac {\tau }{2}}\right)e^{-j2\pi \tau f}\cdot d\tau \,,\end{aligned}}}$

$여기$서 w (${\displaystyle \tau }$) ${\displaystyle w(\tau )}$은(는) 실제 함수임

그리고 나서 우리는 두 조건의 차이를 비교한다.

3 조건

그런 다음 마스크 기능이 있는 상태를 고려한다.

$w{\displaystyle }$ (${\displaystyle \tau }$) ${\displaystyle$ w$(\tau )}$은(는) -B ~ B 사이의 값만 가지고$$ 있으므로 $w{\displaystyle }$(${\displaystyle \tau )}$ ${\displaystyle$ w$(\tau )}$을(를) 사용하여 수행하면 함수의 교차 용어를 제거할 수 있음을$$ 알 수 있다.그러나 x(t)가 델타 함수나 좁은 주파수 함수가 아니라면, 대신 주파수나 리플이 넓은 함수다.신호의 가장자리는 여전히 –B와 B 사이에 있을 수 있으며, 이는 여전히 교차 용어 문제를 야기한다.

예를 들면 다음과 같다.

참고 항목

• 시간 빈도 표현
• 단시간 푸리에 변환
• 스펙트로그램
• 가보르 변환
• 자기 상관
• 가보르-위그너
• 수정된 위그너 분포 함수
• 광학적 등가 정리
• 다항 위너-빌 분포
• 코헨의 클래스 분배 기능
• 위그너 준확률 분포
• 시간 빈도 분석에서 분포 간의 변환
• 이선형 시간-빈도 분포

참조

추가 읽기

• Wigner, E. (1932). "On the Quantum Correction for Thermodynamic Equilibrium" (PDF). Physical Review. 40 (5): 749–759. Bibcode:1932PhRv...40..749W. doi:10.1103/PhysRev.40.749. hdl:10338.dmlcz/141466.
• J. 빌, 1948년"Theri et Applications de la Conception de Signal Analytique", Carbles et Transmission, 2, 61–74.
• T. A. C. M. Classen과 W. F. G. Mecklenbrauker, 1980."위그너 분포 - 시간 주파수 신호 분석을 위한 도구; Part I," 필립스 J. Res, 제35권, 페이지 217–250.
• L. Cohen(1989):IEEE 77 페이지 941–981, 시간 빈도 분포---검토
• L. Cohen, 시간 빈도 분석, 뉴욕 프렌티스 홀, 1995.ISBN 978-0135945322
• S. 첸과 D.Chen, 공동 시간 빈도 분석: 방법 및 적용, 1996년 N.J. 프렌티스 홀 5장
• B. Boashhash, "시간주파수신호분석을 위한 위그너 분포의 사용에 관한 주", IEEE의 음향, 음성 및 신호 처리에 관한 거래, Vol. 36, No. 9, 1518–1521, 1988. doi:10.1109/29.90380.B. Boashash, 편집자, Time-Frequency Signal Analysis and Processing – A Comprehensive Reference, Exvier Science, Oxford, 2003, ISBN 0-08-044335-4.
• F. Hlawatsch, G. F. Boudreaux-Bartels: "선형 및 이차 시간 주파수 신호 표현", IEEE 신호 처리 잡지, 페이지 21–67, 1992년 4월.
• R. L. 앨런과 D.W. 밀스, 신호 분석: 시간, 빈도, 척도 및 구조, Wiley- Interscience, NJ, 2004.
• R. B. 파초리와 A.니샤드, 2016년 120, 페이지 288–304, tunable-Q wavelet transformation, Signal Processing, Vol. 120, 페이지 288–304, terms 감소.
• Jian-Jiun Ding, 시간 빈도 분석 및 웨이브릿 변환 수업 노트, 국립 대만 대학교 전기 공학부, 타이페이, 2015.
• Kakofengitis, D, & Steuernagel, O.(2017).유럽물리저널 플러스 14.07.2017 "약하게 고조된 무조화학적 양자의 양자상 공간 전류"
• R.R. 샤르마와 R.B. 파초리, Wigner-Ville 분배, 회로, 시스템 및 신호 처리에서 교차 터미널을 줄이기 위한 개선된 고유값 분해 기반 접근법, 2018.

외부 링크

위키미디어 커먼즈에는 위그너 유통 기능과 관련된 미디어가 있다.

무료 사전인 Wiktionary에서 wigner 배포 기능을 찾아 보십시오.

• 위그너 분포를 시각적으로 추출하기 위한 GPL 라이선싱 프리웨어에 따른 Sonogram Visible Speech(Sonogram Visible Speech) Visible Speech.