위상최적화

TO(Topology Optimization)는 시스템의 성능을 극대화하기 위해 주어진 하중, 경계 조건 및 제약 조건 세트에 대해 주어진 설계 공간 내의 재료 레이아웃을 최적화하는 수학적 방법입니다.토폴로지 최적화는 미리 정의된 구성을 처리하는 대신 설계 공간 내에서 원하는 형상을 설계할 수 있다는 점에서 형상 최적화 및 크기 최적화와는 다릅니다.

기존의 토폴로지 최적화 공식은 유한 요소 방법(FEM)을 사용하여 설계 성능을 평가합니다.최적성 기준 알고리즘, 점근 이동 방법과 같은 기울기 기반 수학적 프로그래밍 기술 또는 유전 알고리즘과 같은 기울기 기반이 아닌 알고리즘을 사용하여 설계가 최적화됩니다.

위상최적화는 항공우주, 기계, 생명화학 및 토목공학 분야에서 광범위하게 적용되고 있습니다.현재 엔지니어들은 대부분 설계 프로세스의 개념 수준에서 토폴로지 최적화를 사용합니다.자연적으로 발생하는 자유로운 형태로 인해 결과물을 제조하기가 어려운 경우가 많습니다.이러한 이유로 토폴로지 최적화를 통해 발생하는 결과는 제조 가능성에 맞게 미세 조정되는 경우가 많습니다.제조성을 높이기 위해 제형에 제약조건을 추가하는 것은 활발한 연구 분야입니다.어떤 경우에는 토폴로지 최적화의 결과를 적층 제조를 사용하여 직접 제조할 수도 있습니다. 따라서 토폴로지 최적화는 적층 제조 설계의 핵심 부분입니다.

문제명세서

토폴로지 최적화 문제는 일반적인 형태의 최적화 문제로 다음과 같이 쓸 수 있습니다.

${\displaystyle {\begin{aligned}&{\underset {\rho}}{\operatorname {minimize}}}&&F=F(\mathbf {u(\rho),\rho})=\int _{\Omega}f(\mathbf {u(\rho),\rho})\mathrm {d} V\\&G_{0}(\rho )=\int _{\Omega}\rho \mathrm {d} V-V_{0}\leq 0\&G_{j}(\rho)\leq 0{j}}}\leq 0{\mathbf {u}(\rho)=1,...,m\end{aligned}}\leq 0}$

문제 문에는 다음이 포함됩니다.

• 목적 함수 $F{\displaystyle }$( ${\displaystyle u}$ (${\displaystyle \mathbf{}}$ρ${\displaystyle \mathbf{}}$),${\displaystyle \mathbf{}}$ρ${\displaystyle }$) ${\displaystyle$F$(\mathbf {u (\rho ),\rho$}$)$입니다$.$이 함수는 최상의 성능을 위해 최소화하고 있는 양을 나타냅니다.가장 일반적인 목표 기능은 컴플라이언스이며, 컴플라이언스를 최소화하면 구조물의 강성이 최대화됩니다.
• 문제 변수로서의 물질 분포.이것은 각 위치 ρ${\displaystyle }$(${\displaystyle x)}$ ${\displaystyle \rho (\mathbf {x})}$에서 물질의 밀도로 설명됩니다$.$ 물질은 1로 표시되는 존재 또는 0으로 표시되는 부재입니다.${\displaystyle \mathbf{}\mathbf{u}}$ $=$ (${\displaystyle }$$\rho$${\displaystyle }$) ${\displaystyle \mathbf$ =\$mathbf {u} (\mathbf {\rho}$는 ρ ${\displaystyle \rho}$에 따라 선형 또는 비선형 상태 방정식을 만족하는 상태 필드입니다$.$
• 디자인 공간 ($$ω${\displaystyle }$) ${\displaystyle (\Omega )}.$이것은 설계가 존재할 수 있는 허용 부피를 나타냅니다.조립 및 포장 요건, 인적 및 공구 접근성은 이 공간을 식별하는 데 고려해야 할 요소 중 일부입니다.설계 공간의 정의에 따라 최적화 과정에서 수정할 수 없는 모형의 영역 또는 구성요소는 비설계 영역으로 간주됩니다.
• ${\displaystyle m}$ ${\displaystyle \scriptstyle m}$ 제약 조건 ${\displaystyle {Gj}_{}}$(${\displaystyle }$${\displaystyle u}$ (${\displaystyle }$${\displaystyle \rho }$${\displaystyle }$),${\displaystyle \mathrm{\rho }}$) ${\displaystyle \le }$ 0 ${\displaystyle G_{j}(\mathbf {u} (\rho ),\rho )\leq 0}$ 솔루션이 충족해야 하는 특성입니다.예를 들어, 분포할 재료의 최대 양(부피 제약) 또는 최대 응력 값이 있습니다.

$u$ (${\displaystyle \mathbf{}}$ρ${\displaystyle \mathbf{}}$)$${\$displaystyle \mathbf {u(\rho)}}$을(를) 평가하는 것은 종종 미분 방정식을 푸는 것을 포함합니다.이들 방정식에는 알려진 해석적 해가 없기 때문에 유한요소법을 사용하여 가장 일반적으로 수행됩니다.

구현방법론

토폴로지 최적화 문제를 해결하기 위해 사용된 다양한 구현 방법론이 있습니다.

이산형

이산적인 의미에서 토폴로지 최적화 문제를 해결하는 것은 설계 도메인을 유한 요소로 이산화함으로써 수행됩니다.그런 다음 이러한 요소 내부의 물질 밀도를 문제 변수로 취급합니다.이 경우 재료 밀도가 1이면 재료의 존재를 나타내고 0이면 재료의 부재를 나타냅니다.설계의 달성 가능한 위상 복잡성은 요소의 수에 따라 달라지므로 많은 수가 선호됩니다.많은 수의 유한 요소는 달성 가능한 위상 복잡성을 증가시키지만 비용이 듭니다.첫째, FEM 시스템을 해결하는 비용이 더 많이 듭니다.둘째, 다수의 제약 조건을 가진 이산 변수(수천 개의 요소가 드물지 않음)를 처리할 수 있는 알고리즘을 사용할 수 없습니다.또한 모수 변동에 대해 비현실적으로 민감합니다.^[1]문헌에서는 최대 30000개의 변수를 가진 문제가 보고되었습니다.^[2]

연속형 변수로 문제 해결

앞서 언급한 이진 변수를 사용한 토폴로지 최적화 문제 해결의 복잡성으로 인해 커뮤니티는 다른 옵션을 검색하게 되었습니다.하나는 연속형 변수로 밀도를 모델링하는 것입니다.이제 물질 밀도도 0과 1 사이의 값을 얻을 수 있습니다.많은 양의 연속 변수와 다중 제약 조건을 처리하는 그래디언트 기반 알고리즘을 사용할 수 있습니다.그러나 재료 특성은 연속적인 환경에서 모델링해야 합니다.이것은 보간을 통해 이루어집니다.가장 많이 구현된 보간 방법 중 하나는 SIMP(Solid Isotropic Material with Penalization) 방법입니다.^[3][4]이 보간은 기본적으로 거듭제곱 법칙 $E$ = ${\displaystyle E}$ ${\displaystyle 0_{}}$ +${\displaystyle }$ρ ${\displaystyle p^{}}$ (${\displaystyle {}^{}{E}_{}}$ 1${\displaystyle {}_{}}$- ${\displaystyle E_{}}$ 0${\displaystyle {}_{}}$) ${\displaystyle$E\;=\;$E_{0}\,+\,\rho ^{p}(E_{1}-E_{0})}.$물질의 영률을 스칼라 선택 필드에 보간합니다.벌점 파라미터 $p{\displaystyle }$ ${\displaystyle p}$의 값은 일반적으로 $[{\displaystyle 1,}$ ${\displaystyle 3\mathrm{}]}$ ${\displaystyle[1,\,3]}$ 사이에서 취합니다$$$.$ 이것은 재료의 미세 구조를 확인하는 것으로 보여졌습니다.^[5]SIMP 방법에서는 영률의 하한인 E 0 ${\$을 추가하여 밀도가 0이 될 때 목적 함수의 도함수가 ${\displaystyle 0_{}}$이 아님을 확인합니다.페널티 계수가 높을수록 SIMP는 비이진 밀도를 사용할 때 알고리즘에 페널티를 더 많이 부여합니다.불행하게도 처벌 매개변수는 또한 비볼록성을 도입합니다.^[6]

상용 소프트웨어

시중에는 몇 가지 상용 토폴로지 최적화 소프트웨어가 나와 있습니다.대부분 최적의 설계가 어떻게 나타나야 하는지 힌트로 토폴로지 최적화를 사용하고 있으며, 수동 지오메트리 재구성이 필요합니다.첨가제 제조를 위한 최적 설계를 제공하는 몇 가지 솔루션이 있습니다.

예

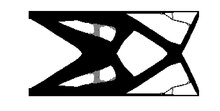
구조준수

이 절에서는 출처를 언급하지 않습니다. 신뢰할 수 있는 자료에 인용문을 추가하여 이 부분을 개선하는 데 도움을 주시기 바랍니다. 출처가 밝혀지지 않은 자료에 이의를 제기하여 제거할 수 있습니다.(2018년 12월) (본 템플릿 메시지 제거 방법 및 시기 알아보기)

뻣뻣한 구조는 일정한 경계 조건이 주어졌을 때 변위가 가장 적게 발생하는 구조입니다.변위에 대한 전역적 측정은 규정된 경계 조건에서 구조물의 변형 에너지(순응성이라고도 함)입니다.변형률 에너지가 낮을수록 구조물의 강성이 높아집니다.따라서 문제의 목적은 변형률 에너지를 최소화하는 것입니다.

넓은 차원에서 볼 때, 재료가 많을수록 하중에 저항할 수 있는 재료가 많아지기 때문에 편향이 줄어든다는 것을 시각화할 수 있습니다.따라서 최적화에는 반대 제약 조건인 볼륨 제약이 필요합니다.이는 실제로는 비용 요소입니다. 왜냐하면 우리는 이 재료에 많은 돈을 쓰고 싶지 않기 때문입니다.사용된 전체 재료를 얻기 위해 볼륨에 대한 선택 필드의 통합을 수행할 수 있습니다.

마지막으로 미분 방정식을 지배하는 탄력성은 최종 문제 진술을 얻기 위해 연결됩니다.

${\displaystyle \min _{\rho}\;\int _{\Omega}{\frac {1}{2}}:\mathbf {\varepsilon} \,\mathrm {d} \Omega }$

대상:

• ${\displaystyle \rho \,\in \,[0,\,1]}$
• ${\displaystyle \int _{\Omega }\rho \,\mathrm {d} \Omega \;\leq \;V^{*}$
• ${\displaystyle \mathbf {\nabla} \cdot \mathbf {\sigma } \,+\,\mathbf {F} \;=\;{\mathbf {0}}}$
• ${\displaystyle \mathbf {\sigma } \;=\;{\mathsf {C}}:\mathbf {\varepsilon}}$

그러나 이러한 문제의 유한 요소 프레임워크에서 간단한 구현은 다음과 같은 문제로 인해 여전히 실행이 불가능합니다.

1. 메쉬 의존성—메쉬 의존성은 한 메쉬에서 얻은 설계가 다른 메쉬에서 얻은 설계가 아님을 의미합니다.그물망이 다듬어질수록 디자인의 특징은 더욱 복잡해집니다.^[7]
2. 수치 불안정성— 체스판의 형태로 지역을 선택합니다.^[8]

이러한 문제들을 완화하기 위해 현재 영상 처리에^[9] 기반한 필터링과 같은 몇몇 기술들이 사용되고 있습니다.이것은 오랫동안 순수하게 휴리스틱 접근법인 것처럼 보였지만, 이러한 방법의 물리적 감각을 뒷받침하기 위해 비국소 탄성에 대한 이론적 연결이 이루어져 왔습니다.^[10]

다중물리학 문제

유체-구조-상호작용

유체-구조-상호작용은 강하게 결합된 현상이며, 정지 또는 이동하는 유체와 탄성 구조 사이의 상호작용에 관한 것입니다.많은 엔지니어링 애플리케이션과 자연 현상은 유체-구조 상호작용의 영향을 받으며, 따라서 이러한 영향을 고려하는 것은 많은 엔지니어링 애플리케이션의 설계에서 매우 중요합니다.유체 구조 상호 작용 문제에 대한 위상 최적화는 예를 들어 참조^[11][12][13] 및 참조에서 연구되었습니다.^[14]다양한 레이놀즈 수에 대해 해결된 설계해는 아래와 같습니다.설계 솔루션은 유체 흐름에 따라 달라지며, 유체와 구조물 사이의 결합이 설계 문제에서 해결됨을 나타냅니다.

열전 변환

열전은 반도전 재료에서 전기 에너지와 열 에너지 사이의 상호작용과 결합에 관한 다중 물리적 문제입니다.열전 에너지 변환은 별도로 확인된 두 가지 효과로 설명할 수 있습니다.제벡 효과와 펠티어 효과.제벡 효과는 열에너지를 전기에너지로 변환하는 것에 관한 것이고 펠티어 효과는 전기에너지를 열에너지로 변환하는 것에 관한 것입니다.^[15]위상최적화 방법론을 적용한 2차원 설계공간에 2개의 열전소재를 공간적으로 분포시킴으로써 열전냉각기 및 열전발전기용 구성 열전소재의 성능을 뛰어넘을 수 있습니다.^[16][17]

강제 3D 프린팅을 따르는 3F3D 형태

최근 3D 프린터 기술의 확산으로 설계자와 엔지니어는 새로운 제품을 설계할 때 토폴로지 최적화 기술을 사용할 수 있게 되었습니다.3D 프린팅과 결합된 토폴로지 최적화를 통해 경량화, 구조 성능 향상 및 설계부터 제조까지의 주기 단축을 실현할 수 있습니다.설계는 효율적이기는 하지만 보다 전통적인 제조 기술로는 실현이 불가능할 수 있습니다.^{[citation needed]}

설계 종속 하중

설계에 의존하는 부하의 방향, 크기 및 위치는 토폴로지 최적화 반복에 따라 달라집니다.따라서 TO 환경에서 이러한 부하를 처리하는 것은 어려운 작업입니다.Refs에서 그러한 부하(예: 압력 부하, 자중 등)를 처리하는 새로운 방법을 찾을 수 있습니다.^[18]

참고문헌

추가열람

• 토폴로지 최적화의 상업적 구현에 있어 최근의 발전.Uwe Schramm, Ming Zhou; 구조, 기계, 재료의 위상설계 최적화에 관한 IUTAM 심포지엄: 상태와 관점, 239-248; 2006 Springer.
• 산업적 구현과 위상최적화의 응용 그리고 미래 요구; Claus B.W. Pedersen; Peter Allinger; 구조, 기계 및 재료의 위상설계 최적화에 관한 IUTAM 심포지엄, 229-238; 2006 Springer.
• 병렬 컴퓨팅 Arash Mahdavi; Balaji Raghavan; Mary Frecker; Int Journal of Structural and Multisciplinary Optimization, Volume 32, 121-132, 2006 Springer
• 위상최적화에 적용된 현대 구조 최적화 개념 Juan Pablo Leiva; Brian C.Watson and Iku Kosaka ; 제40회 AIAA/ASME/ASCE/AHS/ASC 구조, 구조 역학 및 재료 회의.세인트 루이스, 미주리, pp. 1589-1596, 1999

외부 링크

• 토폴로지 최적화 애니메이션