문자열 그래프

String graph

그래프 이론에서 문자열 그래프는 평면에 있는 곡선의 교차 그래프로, 각 곡선을 "끈"이라고 한다.그래프 G에서 G는 한 점에서 세 개의 문자열이 교차하지 않고 그래프가 각 원곡선에 대한 꼭지점과 각 교차 곡선 쌍에 대한 가장자리를 갖는 평면에 그려진 곡선 또는 문자열 집합이 존재하는 경우에만 문자열 그래프다.

배경

시모어 벤저(1959)는 스트링 그래프와 유사한 개념을 유전자 구조에 적용하면서 설명했다.그런 맥락에서 그는 또한 선에 교차하는 간격의 구체적인 사례, 즉 현재 고전적인 구간 그래프 계열을 제시했다.후에 신덴(1966)은 전기 네트워크와 인쇄 회로에 같은 생각을 명시했다.스트링 그래프의 수학 연구는 논문 에를리히, 이븐 & 타르잔(1976년)과 신덴과 로널드 그레이엄의 협업을 통해 시작되었는데, 여기서 마침내 1976년 콤비네토릭스에 관한 제5회 헝가리 콜로키움에서 스트링 그래프의 특성화가 공개 질문으로 제기되었다.[1]그러나 문자열 그래프의 인지도는 결국 NP-완전한 것으로 증명되어 단순한 특성화가 존재할 가능성이 없음을 시사했다.[2]

관련 그래프 클래스

평면 그래프를 문자열 그래프로 표현.

모든 평면 그래프는 문자열 그래프로,[3] 그림에서와 같이 정점 주위와 인접한 각 가장자리의 중간점 주위로 루프되는 각 정점에 대한 문자열을 그려 임의 평면이 포함된 그래프를 나타낼 수 있다.그래프의 모든 에지 uv에 대해 u와 v의 문자열은 uv의 중간점 근처에서 두 번 교차하며, 다른 교차점이 없으므로 교차하는 문자열 쌍은 원래 평면 그래프의 정점 쌍을 정확히 나타낸다.또는 원 패킹 정리에 의해, 모든 평면 그래프는 원의 집합으로 나타낼 수 있으며, 그 중 두 개의 교차점은 해당 정점이 인접한 경우에만 표시할 수 있다. 이러한 원(열린 곡선으로 바꾸기 위해 시작점과 끝점을 선택한 경우)은 주어진 평면 그래프의 문자열 그래프를 나타낸다.찰로핀, 곤살베스 & 오켐(2007)은 모든 평면 그래프는 위에서 설명한 표현과는 달리 각 한 쌍의 문자열들이 최대 하나의 교차점을 갖는 문자열 표현을 가지고 있음을 증명했다.현재 증명된 쉐이너만의 추측은 모든 평면 그래프가 직선 세그먼트의 교차 그래프로 표현될 수 있다는 훨씬 더 강력한 진술로, 이것은 문자열의 매우 특별한 경우다.

문자열 그래프가 아닌 K의5 분할.

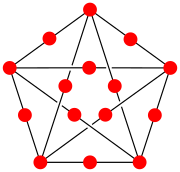
주어진 그래프 G의 모든 가장자리를 세분화하면 G가 평면인 경우에만 결과 그래프가 문자열 그래프가 된다.특히 K는5 평면형이 아니기 때문에 그림에 표시된 전체 그래프 K의5 하위분할은 문자열 그래프가 아니다.[3]

선 세그먼트의 교차 그래프(원 화음)로서 모든 원 그래프도 문자열 그래프다.모든 화음 그래프는 문자열 그래프로 나타낼 수 있다. 화음 그래프는 나무의 하위 트리의 교차 그래프로, 해당 트리의 평면 임베딩과 각 하위 트리를 하위 트리의 가장자리 주변을 추적하는 문자열로 대체함으로써 화음 그래프의 문자열 표현을 구성할 수 있다.

모든 비교가능성 그래프의 보완 그래프도 문자열 그래프다.[4]

기타 결과

에를리히, 이븐 & 타르잔(1976)은 NP-hard가 될 문자열 그래프의 색도 수를 계산하는 것을 보여주었다.Kratochvil(1991a)은 문자열 그래프가 유도된 마이너 폐쇄 클래스를 형성하지만 마이너 폐쇄 클래스의 그래프를 형성하지는 않는다는 것을 발견했다.

모든 m-edge 문자열 그래프는 O(mlogm3/41/2) 정점을 제거하여 두 개의 하위 집합으로 분할할 수 있다.따라서 일부 상수 t에 대한t,t K 하위 그래프가 없는 문자열 그래프인 biclique-free 문자열 그래프는 O(n) 가장자리를 가지며 다항식 확장을 더 강하게 한다.[5]

메모들

  1. ^ 그레이엄(1976년).
  2. ^ Kratochvil (1991b) showed string graph recognition to be NP-hard, but was not able to show that it could be solved in NP. After intermediate results by Schaefer & Štefankovič (2001) and Pach & Tóth (2002), Schaefer, Sedgwick & Štefankovič (2003) completed the proof that the problem is NP-complete.
  3. ^ a b 샤이퍼 & 슈테판코비치(2001)는 이러한 관측을 신덴(1966년)에게 맡긴다.
  4. ^ 골룸빅, 로템앤우루티아(1983)와 로바스츠(1983)이다.Fox & Pach(2010)도 참조하십시오.
  5. ^ Fox & Pach(2010);Dvořak & Norin (2015) 대상 (

참조