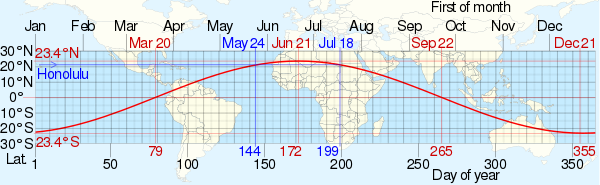
태양 정점각

태양 절정각은 태양 광선과 수직 방향 사이의 각이다. 태양 광선과 수평면 사이의 각도인 태양 고도 각도와 밀접한 관련이 있다. 이 두 각도는 상호 보완적이기 때문에 둘 중 어느 한 각도의 코사인(cosine)은 다른 각도의 사인(sine)과 같다. 구면 삼각측량 결과를 사용하여 둘 다 동일한 공식으로 계산할 수 있다.^[1][2] 태양 정오가 되면, 정점각은 최소한이며, 위도에서 태양 열화 각도를 뺀 것과 같다. 이것은 고대 선원들이 바다를 항해하는 기본이다.^[3]

태양 정점각은 일반적으로 태양 방위각과 조합하여 지구 표면의 주어진 위치에서 관측된 태양의 위치를 결정하기 위해 사용된다.

공식

$\displaystyle \cos \theta _{s}=\sin \alpha _{s}=\sin \Phi \sin \delta +\cos \Phi \cos \cos \cos \delta \cos \cos \cos$

어디에

• ${\displaystyle {\theta }_{}}$ ${\displaystyle s_{}}$ ${\$는 태양 절정각이다.
• ${\displaystyle {\alpha }_{}}$ ${\displaystyle s_{}}$ ${\$는 태양 고도 각도, ${\displaystyle {\alpha }_{}}$ s ${\$\ \$_{s}$ $$= 90° – – ${\displaystyle s_{}}$ ${\$
• ${\displaystyle h}$ $[\displaystyle h}$은(는) 현지 태양 시간에서 시간 각도다.
• ${\displaystyle \Delta }$ ${\displaystyle \delta }$은(는) 태양의 현재 열림이다.
• ${\displaystyle \mathrm{\phi }}$ ${\displaystyle \Phi }$이(가) 로컬 위도다.

서브솔라 포인트와 벡터 분석을 이용한 공식의 도출

이 공식은 코사인 법칙을 정점극-선 구면 삼각형에 적용하여 도출할 수 있지만, 구면 삼각법은 상대적으로 난해한 주제다.

서브솔라 포인트의 좌표를 도입하고 벡터 분석을 이용함으로써 구면 삼각법을 이용하지 않고도 간단한 공식을 얻을 수 있다.^[4]

In the Earth-Centered Earth-Fixed (ECEF) geocentric Cartesian coordinate system, let ${\displaystyle (\phi _{s},\lambda _{s})}$ and ${\displaystyle (\phi _{o},\lambda _{o})}$ be the latitudes and longitudes, or coordinates, of the subsolar point and the observer's point, then the upward-pointi$s{\displaystyle \mathbf{}}$ ${\$과($)$ ${\displaystyle V_{}}$o z {\$displaystyle$ \$mathbf {V} _{oz$} 두 지점의 ng 단위 벡터는 다음과 같다$.$

${\displaystyle \mathbf {S} =\cos \phi _{s}\cos \lambda _{s}{\mathbf {i} }+\cos \phi _{s}\sin \lambda _{s}{\mathbf {j} }+\sin \phi _{s}{\mathbf {k} }}$,

${\displaystyle \mathbf {V} _{oz}=\cos \phi _{o}\cos \lambda _{o}{\mathbf {i} }+\cos \phi _{o}\sin \lambda _{o}{\mathbf {j} }+\sin \phi _{o}{\mathbf {k} }}$.

여기서 $i{\displaystyle \mathbf{}}$ ${\$ $j{\displaystyle \mathbf{}}$ ${\${\$mathbf {j}}$ 및$$ $k{\displaystyle \mathbf{}}$ ${\$은 ECEF 좌표계의 기본 벡터다$$.

이제 태양 정점각의 코사인 $\theta {\displaystyle {}_{}}$ ${\displaystyle s_{}}$ ${\$는 단순히 위의 두 벡터의 도트 곱이다.

${\displaystyle \cos \theta _{s}=\mathbf {S} \cdot \mathbf {V} _{oz}=\sin \phi _{o}\sin \phi _{s}+\cos \phi _{o}\cos \phi _{s}\cos(\lambda _{s}-\lambda _{o})}$.

$\varphi {\displaystyle {}_{}}$ ${\displaystyle s_{}}$ ${\$는 태양의 부호인$$$\Delta {\displaystyle }$ ${\displaystyle \delta }$과 동일하며, ${\displaystyle {\lambda }_{}}$ s -${\displaystyle {}_{}{}_{}}$ ${\displaystyle o_{}}$ ${\$ $_$$\{$$o$$}$는 $앞$에서 정의한 시간 각도인${\displaystyle }$- h ${\$${\displaystyle h}$}과 동일하다는 점에 유의한다. 그래서 위의 형식은 앞에서 주어진 형식과 수학적으로 동일하다.

또한, Ref.는 구면 삼각법을 사용하지 않고 태양 방위각의 공식을 유사한 방식으로 도출했다.

최소 및 최대

At any given location on any given day, the solar zenith angle, ${\displaystyle \theta _{s}}$, reaches its minimum, ${\displaystyle \theta _{min}}$, at local solar noon when the hour angle ${\displaystyle h=0}$, or ${\displaystyle \lambda _{s}-\lambda _{o}=0}$, namely, ${\displaystyle \cos }$${\displaystyle \cos \theta _{min}=\cos( \phi _{o}-\phi _{s} )}$, or ${\displaystyle \theta _{min}= \phi _{o}-\phi _{s} }$. If ${\displaystyle \theta _{min}>90^{\circ }}$, it is polar night.

And at any given location on any given day, the solar zenith angle, ${\displaystyle \theta _{s}}$, reaches its maximum, ${\displaystyle \theta _{max}}$, at local midnight when the hour angle ${\displaystyle h=-180^{\circ }}$, or ${\displaystyle \lambda _{s}-\$람다 _{제일의 것이다}=-180^{\circ}}, 즉⁡ θ m는 x=cos⁡(o 180∘− ϕ+ϕ s){\displaystyle \cos \theta_{맥스}(180^{\circ}-\phi_{시}+\phi_{s})}, 또는 o x=180∘− ϕ m θ+sϕ{\displaystyle \theta_{맥스}=180^{\circ}- \phi _{제일의 것이다}+\phi _{s}}. 만약 θ x<>90∘ 거.$극지방날$이다

주의사항

계산된 값은 공통/지질 위도와 지리 중심 위도의 구분에 따른 근사값이다. 그러나 두 값은 원호의 12분 미만으로 차이가 나 태양의 겉보기 각반경보다 작다.

이 공식은 또한 대기 굴절의 효과를 무시한다.^[5]

적용들

일출/일몰

일몰 및 일출(약)은 정점 각도가 90°일 때 발생하며, 여기서 시간 각 h가₀ 만족한다^[2].

$\displaystyle \cos h_{0}=-\tan \Phi \tan \delta .}$

일몰과 일출의 정확한 시간은 대기에 의해 굴절된 태양의 상지가 수평선상에 나타날 때 발생한다.

알베도

지구의 지역 알베도를 계산하는 데 사용되는 가중 일일 평균 정점각은 다음과 같다.

${\displaystyle {\cos \cos \theta _{s}={\frac {\int_{h_{0}^{0}}Qcos \cos \theta _{s}{\text{d}h}}{0}^_{0}Q{d}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

여기서 Q는 순간 방사조도다.^[2]

특수 각도의 요약

예를 들어, 태양 입면각은 다음과 같다.

• 적도에 있을 경우 90°, 분천일, 태양시간 12시
• 일몰이나 일출에 0도 가까이
• -90°에서 0° 사이의 야간(낮음)

태양의 위치에 정확한 계산이 주어진다. 다른 근사치들은 다른 곳에 존재한다.^[6]

참고 항목

• 방위각
• 태양 방위각
• 수평좌표계
• 궤도 목록
• 태양의 위치
• 태양길
• 일출
• 일몰
• 일출시간

참조