공정능력지수

공정 개선 노력에서 공정 능력 지수 또는 공정 능력 비율은 공정 능력의 통계적 척도로, 즉 규격 한계 내에서 공정을 산출할 수 있는 공정 능력이다.^[1] 공정 능력의 개념은 통계적 통제 상태에 있는 공정에만 의미를 부여한다. 공정 능력 지수는 한 공정이 규격 한계와 비교하여 얼마나 많은 "자연적 변화"를 경험하는지 측정하고, 조직이 이를 얼마나 잘 통제하는지와 관련하여 다른 공정을 비교할 수 있도록 한다.

비전문가의 예

한 회사가 선반에서 공칭 직경 20 mm의 차축을 생산한다. 어떤 차축도 정확히 20 mm까지 만들 수 없으므로 설계자는 허용 가능한 최대 편차(허용 오차 또는 규격 한계라고 함)를 지정한다. 예를 들어 차축이 19.9 ~ 20.2 mm 사이여야 하는 요건이 될 수 있다. 공정 능력 지수는 생산된 차축이 이 요건을 충족할 가능성을 나타내는 척도다. 지수는 통계적(자연적) 변동에만 관련된다. 이것들은 특정한 원인 없이 자연스럽게 일어나는 변화들이다. 다루지 않은 오류에는 오퍼레이터 오류가 포함되거나 선반의 메커니즘에서 재생되어 잘못되거나 예측할 수 없는 툴 위치가 발생한다. 후자의 오차가 발생하면 그 과정은 통계적 통제 상태가 아니다. 이럴 때 공정능력지수는 의미가 없다.

소개

공정의 규격 상한과 하한이 USL과 규격 하한인 경우, 공정 평균은 T이고 공정의 추정 평균은 ${\hat {\mu }}$ ${\$ 이고 ${\hat {\mu }}$ 공정의 추정 변동성(표준 편차로 표현됨)은 ^ ${\hat {\sigma }}$ ${\$ 이고 ${\hat {\sigma }}$ 그 다음 일반적으로 받아들여진다. 공정 능력 지수:

색인	설명
${\hat{C}_{p}={\frac {\text{USL - LSL}}{6{\hat {\sigma }}$	공정 평균이 규격 한계 사이에 중심화되어 있는 경우 공정이 생산할 수 있는 것을 추정한다. 공정 출력이 대략 정규 분포를 따른다고 가정한다.
${\hat{C}_{p,{\text{lower}}={\hat{\mu}-{\text}}LSL}} \{\hat{\sigma }}}}}}$	하한(예: 강도)으로만 구성된 규격에 대한 공정 능력을 추정한다. 공정 출력이 대략 정규 분포를 따른다고 가정한다.
${\hat{C}_{p,{\text{upper}}={\text{{\text}}USL}-{\hat{\mu }}}3{\hat{\sigma }}}}}}}이상 \hat {\sigma }}}$	상한(예: 농도)으로만 구성된 규격에 대한 공정 능력을 추정한다. 공정 출력이 대략 정규 분포를 따른다고 가정한다.
${\hat{C}_{pk}=\min {\Bigg [}{\text{}USL}-{\hat {\mu }}3{\hat {\sigma }}},{{\hat {\mu }-{\text{LSL}} \{\hat {\sigma }}{\Bigg ]}}}}$	공정 평균이 규격 한계 사이에 중심화되어 있지 않을 수 있다는 점을 고려하여 공정이 생산할 수 있는 것을 추정한다. (공정 평균이 중심화되어 있지 않으면 ${\hat {C}}_{p}$ ${\hat {C}}_{p}$ p ${\$ 공정 능력을 과대평가한다 ${\hat {C}}_{p}$ .) ${\hat {C}}_{pk}<0$ ${\hat {C}}_{pk}<0$ ${\hat {C}}_{pk}<0$ ${\hat {C}}_{pk}<0$ < ${\hat {C}}_{pk}<0$ ${\displaystyle {\c$ }_ ${pk}<0}$ 공정 $평균$ 이 규격 한계를 벗어나는 경우 ${\hat {C}}_{pk}<0$ . 공정 출력이 대략 정규 분포를 따른다고 가정한다.
${\c}_{pm}={\frac {{\hat{C}}_{p}{\sqrt{1+\왼쪽({\frac {{\hat{\mu{}-T}{\hat{\sigma}}}}}}{2}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$	대상 주위의 공정 능력 추정치 T. C ${\hat {C}}_{pm}$ p ${\hat {C}}_{pm}$ ${\$ 은(는) 항상 0보다 크다 ${\hat {C}}_{pm}$ . 공정 출력이 대략 정규 분포를 따른다고 가정한다. ${\hat {C}}_{pm}$ ${\hat {C}}_{pm}$ ${\hat {C}}_{pm}$ ${\hat {C}}_{pm}$ ${\$ 은 ${\hat {C}}_{{pm}}$ (는) 타구치 능력 지수라고도 한다.^[2]
${\c}_{pkm}={\frac {{\hat {{C}_{pk}{\sqrt{1+\왼쪽({\frac {{\mu{}-T}{\hat{\sigma}}}}{\sigma}\rigma}^{2}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$	목표값, T 주변의 공정 능력을 추정하며 중심 이외의 공정 평균을 설명한다. 공정 출력이 대략 정규 분포를 따른다고 가정한다.

${\hat {\sigma }}$ ${\hat {\sigma }}$ ${\$ 은(는) 샘플 표준 편차를 사용하여 추정한다 ${\hat {\sigma }}$ .

권장 값

공정 능력 지수는 점점 더 높은 값으로 더 바람직한 공정 능력을 표현하기 위해 구성된다. 0에 가깝거나 낮은 값은 목표물을 벗어난 공정( ${\hat {\mu }}$ ${\$ 또는 높은 변동성을 나타낸다.

최소한의 "허용 가능한" 공정능력 목표치에 대한 가치를 고정하는 것은 개인적인 의견의 문제로서, 어떤 공감대가 존재하는지는 고려 중인 산업, 시설, 프로세스에 따라 다르다. 예를 들어 자동차 산업에서 자동차 산업 행동 그룹은 중요-품질 공정 특성에 대한 권장 C_pk 최소값에 대한 4번째 판의 생산 부품 승인 프로세스에 지침을 제시한다. 그러나 이러한 기준은 논쟁의 여지가 있으며, 단지 적절하게 평가되지 않았다는 이유만으로 몇 가지 프로세스가 능력에 대해 평가되지 않을 수 있다.

공정능력은 규격의 함수이기 때문에 공정능력지수는 규격에 버금간다. 예를 들어, 해당 규격이 부품의 기능과 중요도를 고려하지 않고 엔지니어링 가이드라인에서 나온 것이라면, 공정 능력에 대한 논의는 무용지물이며, 부품 경계선이 사양을 벗어나는 실제 위험성에 초점을 맞추면 더 많은 이익을 얻을 수 있다. 타구치의 손실 함수는 이 개념을 더 잘 보여준다.

적어도 한 명의 학계 전문가가 다음^[3] 사항을 권고한다.

상황	양면 사양에 대해 권장되는 최소 공정 능력	단측 사양에 대해 권장되는 최소 공정 능력
기존공정	1.33	1.25
신규공정	1.50	1.45
기존 프로세스에 대한 안전 또는 중요 매개 변수	1.50	1.45
새 프로세스에 대한 안전 또는 중요 매개 변수	1.67	1.60
식스 시그마 품질공정	2.00	2.00

그러나 공정 능력 지수가 2.5보다 큰 특성을 갖는 공정의 경우 불필요한 정밀도는 비쌀 수 있다.^[4]

공정 낙진 측정과의 관계

C와_pk 같은 공정 능력 지수에서 공정 낙진 측정에 대한 매핑은 간단하다. 공정 낙진은 공정이 얼마나 많은 결점을 생산하고 DPMO 또는 PPM으로 측정하는지 계량한다. Process yield is the complement of process fallout and is approximately equal to the area under the probability density function $\Phi (\sigma )={\frac {1}{\sqrt {2\pi }}}\int _{-\sigma }^{\sigma }e^{-t^{2}/2}\,dt$ if the process output is approximately normally 분산된

단기("짧은 시그마")에서 관계는 다음과 같다.

C_p	시그마 수준(σ)	아래 영역 확률밀도함수 $Phi(\displaystyle \Phi(\sigma )}$	공정수익률	공정낙진 (DPMO/PPM 측면에서)
0.33	1	0.6826894921	68.27%	317311
0.67	2	0.9544997361	95.45%	45500
1.00	3	0.9973002039	99.73%	2700
1.33	4	0.9999366575	99.99%	63
1.67	5	0.9999994267	99.9999%	1
2.00	6	0.9999999980	99.9999998%	0.002

장기적으로는 공정이 크게 이동하거나 표류할 수 있다(대부분의 관리도는 공정 출력에서 1.5㎛ 이상의 변화에만 민감하다). 프로세스에서 1.5 시그마 시프트가 목표값에서 1.5km 떨어진 경우(식스 시그마 참조) 다음과 같은 관계를 생성한다.^[5]

C_p	조정됨 시그마 수준(σ)	아래 영역 확률밀도함수 $Phi(\displaystyle \Phi(\sigma )}$	공정수익률	공정낙진 (DPMO/PPM 측면에서)
0.33	1	0.3085375387	30.85%	691462
0.67	2	0.6914624613	69.15%	308538
1.00	3	0.9331927987	93.32%	66807
1.33	4	0.9937903347	99.38%	6209
1.67	5	0.9997673709	99.9767%	232.6
2.00	6	0.9999966023	99.99966%	3.40

공정은 상당히 장기간 이동하거나 표류할 수 있기 때문에 각 공정은 고유한 시그마 이동 값을 가질 수 있으므로 공정 능력 지수는 통계적 통제를 요구하기 때문에 덜 적용할 수 있다.

예

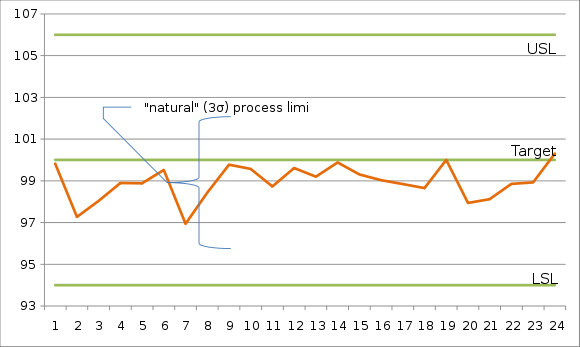
목표값이 100.00μm이고 규격 상한과 하한이 각각 106.00μm, 94.00μm인 품질 특성을 고려한다. 공정을 잠시 주의 깊게 관찰한 후 공정이 관리 상태에 있고 예측 가능한 출력을 생성하는 것으로 나타날 경우(아래 런 차트에서 나타냄) 평균 및 표준 편차를 의미 있게 추정할 수 있다.

${\hat {\mu }}$ ${\$ 과( ${\hat {\sigma }}$ μ $^$ {\ $displaystyle$ {\ $hat$ {\ $sigma$ }}이(가 ${\hat {\sigma }}$ ) 각각 98.94μm와 1.03μm로 추정되면 다음과 같다.

색인
${\hat{C}_{p}={\frac {\text{USL - LSL}}{6{\hat {\sigma }}}}}}{{\frac {106.00-94.00}{6\time 1.03}=1.94$
${\hat{C}_{pk}=\min {\Bigg [}{\text{}USL}-{\hat {\mu }}3{\hat {\sigma }}},{{\hat {\mu }-{\text{LSL} \{\hat {\sigma }}{\Bigg ]}=\min [}{106.00-98.94 \3\time 1.03}{98.94-94 \3\time 1.03}{\Bigg ]}=1.60$
${\hat {C}}_{pm}={\frac {{\hat {C}}_{p}}{\sqrt {1+\left({\frac {{\hat {\mu }}-T}{\hat {\sigma }}}\right)^{2}}}}={\frac {1.94}{\sqrt {1+\left({\frac {98.94-100.00}{1.03}}\right)^{2}}}}=1.35$
${\hat {C}}_{pkm}={\frac {{\hat {C}}_{pk}}{\sqrt {1+\left({\frac {{\hat {\mu }}-T}{\hat {\sigma }}}\right)^{2}}}}={\frac {1.60}{\sqrt {1+\left({\frac {98.94-100.00}{1.03}}\right)^{2}}}}=1.11$

공정이 중심에서 벗어나(목표값보다 약 1㎞ 낮음) 실행되고 있다는 사실은 C_p, C_pk, C_pm, C의_pkm 현저하게 다른 값에 반영된다.

참고 항목

참조

^ "What is Process Capability?". NIST/Sematech Engineering Statistics Handbook. National Institute of Standards and Technology. Retrieved 2008-06-22. 외부 링크 위치 work= (도움말)
^ Boyles, Russell (1991). "The Taguchi Capability Index". Journal of Quality Technology. 23 (1). Milwaukee, Wisconsin: American Society for Quality Control. pp. 17–26. ISSN 0022-4065. OCLC 1800135.
^ Montgomery, Douglas (2004). Introduction to Statistical Quality Control. New York, New York: John Wiley & Sons, Inc. p. 776. ISBN 978-0-471-65631-9. OCLC 56729567. Archived from the original on 2008-06-20.
^ Booker, J. M.; Raines, M.; Swift, K. G. (2001). Designing Capable and Reliable Products. Oxford: Butterworth-Heinemann. ISBN 978-0-7506-5076-2. OCLC 47030836.
^ "Sigma Conversion Calculator BMGI.org". bmgi.org. Archived from the original on 2016-03-16. Retrieved 2016-03-17.

[1] "What is Process Capability?". NIST/Sematech Engineering Statistics Handbook. National Institute of Standards and Technology. Retrieved 2008-06-22. 외부 링크 위치 work= (도움말)

[2] Boyles, Russell (1991). "The Taguchi Capability Index". Journal of Quality Technology. 23 (1). Milwaukee, Wisconsin: American Society for Quality Control. pp. 17–26. ISSN 0022-4065. OCLC 1800135.

[3] Montgomery, Douglas (2004). Introduction to Statistical Quality Control. New York, New York: John Wiley & Sons, Inc. p. 776. ISBN 978-0-471-65631-9. OCLC 56729567. Archived from the original on 2008-06-20.

[4] Booker, J. M.; Raines, M.; Swift, K. G. (2001). Designing Capable and Reliable Products. Oxford: Butterworth-Heinemann. ISBN 978-0-7506-5076-2. OCLC 47030836.

[5] "Sigma Conversion Calculator BMGI.org". bmgi.org. Archived from the original on 2016-03-16. Retrieved 2016-03-17.

[1]

[2]

[3]

[4]

[5]

Search

공정능력지수

네임스페이스

더

목차

비전문가의 예

소개

권장 값

공정 낙진 측정과의 관계

예

참고 항목

참조