개방 회로 시간 상수법

개방 회로 시간 상수(OCT) 방법은 복잡한 회로의 코너 주파수를 결정하기 위해 전자 회로 설계에 사용되는 대략적인 분석 기법이다. 반응성 소자가 콘덴서만으로 구성되었을 때 0-값 시간 상수(ZVT) 방법 기법의 특수한 경우다. 영값 시간(ZVT) 상수법 자체는 인덕터와 캐패시터를 모두 시간 상수와 전송 상수를 사용하여 반응성 요소로 사용하는 모든 LTI 시스템의 0과 극을 완전하게 평가할 수 있는 일반 시간 및 전달 상수(TTC) 분석의 특수한 경우다. OCT 방법은 신속한 평가를 제공하며, 회로 개선의 지침으로서 시간 상수에 대한 가장 큰 기여를 식별한다.

이 방법의 기본은 앰프의 코너 주파수가 주파수에서 선형인 전달 함수의 분모에 있는 항에 의해 결정된다는 근사값이다. 이 근사치는 분자의 0이 주파수에 가까운 경우에 극히 부정확할 수 있다.^[1]

또한 이 방법은 회로 내 각 콘덴서에 대한 RC-제품의 합계를 바탕으로 주파수에서 선형이라는 용어를 찾는 단순화된 방법을 사용한다. 여기서 선택한 콘덴서에 대한 저항 R은 테스트 소스를 현장에 삽입하고 다른 모든 콘덴서를 0으로 설정하여 찾은 저항이다. 따라서 0-값 시간 상수 기법이라는 명칭은 다음과 같다.

예제: 단순 RC 네트워크

그림 1: 시간 상수를 찾기 위한 간단한 RC 회로 및 보조 회로

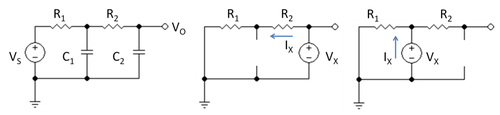
그림 1은 간단한 RC 로우패스 필터를 보여준다. 그것의 이전 기능은 다음과 같이 Kirchhoff의 현행법을 이용하여 발견된다. 출력할 때,

${\displaystyle {\frac {V_{1}-V_{O}{R_{2}}:j\omega C_{2}V_{O}\,}$

여기서 V는₁ 커패시터 C의₁ 상단에 있는 전압이다. 중앙 노드:

${\displaystyle {\v_{S}-{1}-{1}:{R_{1}:{1}=j\omega C_{1}V_{1}+{\frac {V_{1}-{O}{R_{2}}\}\}}}}$

이러한 관계를 결합하여 전달 함수는 다음과 같은 것으로 확인된다.

${\displaystyle {\frac {V_{O}}{V_{S}}}={\frac {1}{1+j\omega \left(C_{2}(R_{1}+R_{2})+C_{1}R_{1}\right)+(j\omega )^{2}C_{1}C_{2}R_{1}R_{2}}}}$

이 전달함수에서 Ω의 선형 항은 이 예에 개방 회로 시간 상수법을 적용한 다음과 같은 방법으로 도출할 수 있다.

1. 신호 소스를 0으로 설정하십시오.
2. 캐패시터 C를₂ 선택하고 테스트 전압 V로_X 교체한 후 C를₁ 개방 회로로 교체하십시오. 그 후 시험 전압에 의해 보이는 저항은 그림 1의 중간 패널에 있는 회로를 사용하여 발견되고 간단히 V_X/I_X = R₁ + R이다₂. 제품₂ C (R₁₂ + R )를 형성한다.
3. 캐패시터 C를₁ 선택하고 테스트 전압 V로_X 교체한 후 C를₂ 개방 회로로 교체하십시오. 그 후 시험 전압에 의해 보이는 저항은 그림 1의 오른쪽 패널에 있는 회로를 사용하여 발견되고 간단히 V_X/I_X1 = R. 제품 C R을₁₁ 형성한다.
4. 이 용어를 추가하십시오.

사실상 다른 콘덴서가 개방 회로일 때 각 콘덴서가 회로에서 발견되는 저항을 통해 충전 및 방전되는 것과 같다.

개방 회로 시간 상수 절차는 RC 네트워크가 얼마나 복잡해지는지에 관계없이 선형 용어를 Ω으로 제공한다. 이것은 원래 쏜튼과 서얼의 출입 행렬의 공동 요소를 계산하여 개발되고 증명되었다.^[2] 이것(및 TTC의 다른 특성)에 대한 보다 직관적인 귀납적 증거는 나중에 하지미리에 의해 개발되었다.^[3]

복잡한 회로의 경우 이 절차는 회로의 모든 캐패시터를 통과하여 위의 규칙을 따르는 것으로 구성된다. 보다 일반적인 파생은 그레이와 마이어에서 찾아볼 수 있다.^[4]

지금까지 결과는 일반적이지만, 이 결과를 활용하기 위해 근사치가 도입된다. 즉, 이 선형 항 Ω이 회로의 코너 주파수를 결정한다고 가정한다.

그러한 가정은 그림 1의 예를 사용하여 더 면밀하게 조사할 수 있다: 이 회로의 시간 상수가 τ과₁ τ이라고₂ 가정한다. 즉, 다음과 같다.

${\displaystyle \left(1+j\omega {\tau }_{1})(1+j\omega {\tau }_{2}\right)=1+j\omega \left(C_{2}(R_{1}+R_{2})+C_{1}R_{1}\right)+(j\omega )^{2}C_{1}C_{2}R_{1}R_{2}}$

선형 항과 2차 항의 계수를 Ω으로 비교하면 다음과 같은 결과가 나타난다.

${\displaystyle \tau _{1}+\tau _{2}=C_{2}(R_{1}+R_{2})+C_{1}R_{1}\,}$

${\displaystyle \tau _{1}\tau _{2}=C_{1}C_{2}R_{1}R_{1}R_{2}\ .}$

두 개의 시간 상수 중 하나가 가장 길 것이다. ;으로₁ 하자. 순간적으로 다른 것보다도₁ 훨씬 크다고 가정해 보자, > >> τ₂. 이 경우 근사치에는 다음이 포함된다.

${\displaystyle \tau _{1}+\tau _{2}\reason \tau _{1}\,}$

그리고

${\displaystyle \tau_{2}={\frac {\tau_{1}{1}\tau_{1}}}\preck {\tau_{1}{1}}\pau_{1}{1}+\tau_{2}}\}\}\}\}\}\}\}\}\}}}}\$

즉, RC 값을 대체한다.

${\displaystyle \tau _{1}\chat {\tau _{1}}=\\tau _{1}+C_{2}(R_{1}+R_{2})+C_{1}R_{1}\}\,}$

그리고

${\displaystyle \tau _{2}\approx {\hat {\tau _{2}}}={\frac {\tau _{1}\tau _{2}}{\tau _{1}+\tau _{2}}}={\frac {C_{1}C_{2}R_{1}R_{2}}{C_{2}(R_{1}+R_{2})+C_{1}R_{1}}}\ ,}$

여기서 ( ^ )는 대략적인 결과를 나타낸다. 또한 회로 시간 상수는 둘 다 캐패시터를 포함하며, 다시 말하면 일반적으로 회로 시간 상수는 단일 캐패시터에 의해 결정되지 않는다. 이러한 결과를 이용하여 코너 주파수(3dB 주파수)가 얼마나 잘 주어지는지 쉽게 탐색할 수 있다.

${\displaystyle f_{3dB}={\frac {1}{2\pi {\hat {\tau_{1}},}$

그림 2: 실제 극 위치와 OCTC 추정치 비교

매개 변수가 다양한 만큼 또한, 정확한 전달 함수는 대략적인 것, 즉,

${\displaystyle {\frac {1}{(1+j\omega \tau _{1})(1+j\omega \tau _{2})}}\ }$ ${\displaystyle \ }$ with ${\displaystyle \ }$ ${\displaystyle \ {\frac {1}{(1+j\omega {\hat {\tau _{1}}})(1+j\omega {\ha$$t {\tau _{2}}}\ .}$

물론 가정 τ₁ >> τ이₂ 정확할 때는 동의가 좋다.

그림 2는 근사치를 나타낸다. x축은 로그 척도의 비율 τ₁ / τ이다₂. 이 변수의 증가는 높은 극이 코너 주파수보다 훨씬 위에 있다는 것을 의미한다. y축은 실제 시간 상수에 대한 OCTC(개방 회로 시간 상수) 추정치의 비율이다. 가장 낮은 극의 경우 곡선 T_1을 사용하고, 이 곡선은 모서리 주파수를 참조하며, 높은 극의 경우 곡선 T_2를 사용한다. 최악의 합의는 τ₁ = τ에₂ 대한 것이다. 이 경우 τ^{^}₁ = 2τ이고₁ 코너 주파수는 2의 인자가 너무 작다. 높은 극은 너무 높은 2개의 요인이다(시간 상수는 실제 값의 절반이다).

모든 경우에, 추정된 코너 주파수는 실제 코너에서 2의 요인보다 가깝고, 항상 보수적이어서, 실제 회로는 예측된 것보다 더 잘 동작할 것이다. 그러나 높은 극은 항상 낙관적이다. 즉, 실제보다 높은 주파수로 높은 극을 예측한다. 이 추정치를 2극 주파수 비율에 따라 달라지는 단계 반응 예측에 사용하기 위해(예: 극 분할에 관한 기사 참조), 그림 2는 τ과^{^}₁ τ의^{^}₂ 오차가 τ^{^}₁/τ의^{^}₂ 비율에서 서로 강화되기 때문에 정확성을 위해 상당히 큰 τ₁/τ의₂ 비율이 필요하다는 것을 제안한다.

개방 회로 시간 상수 방법은 코너 주파수에만 초점을 맞추지만, 위에서 본 바와 같이 더 높은 극에 대한 추정도 가능하다.

다수의 단일 트랜지스터 증폭기 단계에 개방 회로 시간 상수법을 적용하는 방법은 Pittet과 Kandaswamy에서 확인할 수 있다.^[5]

참조 및 참고 사항