양파

양파는 단단한 판이나 구에서 번식한다.^[1] 그것들은 입자 운동이 파동 전파 방향과 평면 정상(판과 수직인 방향)을 포함하는 평면에 있는 탄성파다. 1917년 영국의 수학자 호레이스 램은 이런 유형의 음향파에 대한 고전적 분석과 설명을 발표했다. 그들의 재산은 꽤 복잡한 것으로 밝혀졌다. 무한 매체는 고유한 속도로 이동하는 두 개의 파장 모드만 지원하지만, 판은 파장과 판 두께의 관계에 따라 속도가 달라지는 두 개의 무한대의 양파 모드를 지원한다.

1990년대 이후 양파의 이해와 활용은 컴퓨팅 파워의 이용가능성이 급속도로 높아진 덕택에 크게 진전되었다. 램의 이론적 제형은 특히 비파괴 시험 분야에서 실질적인 실용화를 발견했다.

레일리-램파라는 용어는 단일 표면을 따라 전파되는 파동의 일종인 레일리파를 수용한다. Rayleigh 와 Lamb 파동 모두 그들을 안내하는 표면의 탄성 성질에 의해 구속된다.

양의 특성 방정식

일반적으로 고체 물질의^[2] 탄성 파동은 그들이 전파하는 매체의 경계에 의해 유도된다. 물리적 음향학에서 널리 사용되는 유도파 전파 접근방식은 구조 기하학을 대표하는 경계 조건에 따라 선형 탄성파에 대한 파동 방정식에 대한 사인파 해결책을 모색하는 것이다. 이것은 전형적인 고유치 문제다.

접시 속의 파도는 이런 방식으로 분석된 최초의 유도파 중 하나였다. 이 분석은 1917년^[3] 당시 수학물리학의 리더였던 호레이스 램에 의해 개발되어 출판되었다.

양의 방정식은 x와 y 방향으로 무한 범위를 갖는 고체 판에 대한 형식주의를 설정하고, z 방향으로 두께 d를 설정함으로써 도출되었다. 파형 방정식에 대한 사인파 용액은 형태 X와 Z 변위를 갖는 것으로 가정되었다.

${\displaystyle \xi =A_{x}f_{x}(z)e^{i(\omega t-kx)}\quad \quad (1)}$

${\displaystyle \제타 =A_{z}f_{z}(z)e^{i(\omega t-kx)}\quad \quad (2)}$

이 형태는 파장 2㎛/k, 주파수 Ω/2㎛로 x방향으로 전파되는 정현파를 나타낸다. 변위는 x, z, t만의 함수로서, y 방향에는 변위가 없고 y 방향에는 물리적 수량의 변동이 없다.

플레이트의 자유 표면에 대한 물리적 경계 조건은 z = +/- d/2에서 z 방향의 응력 성분이 0이라는 것이다. 이 두 조건을 파형 방정식에 대한 위의 공식화된 해법에 적용하면, 한 쌍의 특성 방정식을 찾을 수 있다. 다음은 다음과 같다.

${\displaystyle {\frac {\tanh(\d/2)}{\tanh(\d/2)}}}={\frac {4\cHB \cHB \cHB \cHB \cHB \{2}}{{2}}}{(k^{2}+\^{2})}}}\\\\\\\\\cHB \cHB \CHB \cHB \3}$

대칭 모드의 경우

${\displaystyle {\frac {\tanh(\d/2)}{\tanh(\d/2)}}}={\frac {(k^{2}+\cHB^{2}}^{2}}:{4\i1\i1\i1\\i1\i1\\i1\i1\i1\i1\i1\i1\i1\i1\i1\i1\i1\i4}}}$

비대칭 모드의 경우, 다음과 같이 하십시오.

${\displaystyle \c_{{l}^{2}-{\frac {\c_{l}^{2}}:}\reason \reason {\text{and}}}\reason \i1}{2}-{\frac}-{c_{t}^{2}}.}$

이러한 방정식에 내재된 것은 각도 주파수 Ω과 파형 번호 k 사이의 관계다. d/d 또는 fd. c와_l c의_t 함수가 각각 종파 및 전단파 속도이기 때문에 위상 속도 c_p = f f = Ω/k, 그룹 속도 c_g = dΩ/dk를 찾기 위해 수치적 방법을 사용한다.

또한 이러한 방정식의 해법은 (1)과 (2)가 일반적인 형태로만 나타내는 입자 운동의 정확한 형태를 드러낸다. 등식 (3)은 판의 중간면(평면 z = 0)을 중심으로 움직임이 대칭인 파동 계열을, 등식(4)은 중간면 반대칭인 파동 계열을 발생시키는 것으로 밝혀졌다. 그림 1은 각 가족의 구성원을 보여준다.

램의 특성 방정식은 무한 플레이트에서 전파되는 파동에 대해 확립되었다. - 어떤 파동에너지도 전파할 수 없는 두 개의 평행 평면에 의해 경계된 균질하고 등방성 고체. 램은 자신의 문제를 공식화하면서 입자 움직임의 구성요소를 판의 정상 방향(z 방향)과 파장의 전파 방향(x 방향)으로 제한했다. 정의상 양파는 y방향의 입자운동이 없다. 판의 y방향 모션은 이른바 SH 또는 전단수평파 모드에서 찾을 수 있다. 이러한 방향은 x 방향 또는 z 방향에서 움직임이 없으므로 양파 모드를 보완한다. 이 두 가지 파형은 위에서 정의한 대로 판에 일직선, 무한대 파선으로 전파할 수 있는 유일한 파형이다.

특성 방정식에 내재된 속도 분산

양파는 속도 분산을 나타낸다. 즉, 양파의 전파 속도는 재료의 탄성 상수와 밀도뿐만 아니라 주파수(또는 파장)에 따라 달라진다. 이 현상은 판의 파동 행동을 연구하고 이해하는 데 중심적이다. 물리적으로 핵심 매개변수는 판 두께 d 대 파장 ${\displaystyle \lambda }}$이다$.$ 이 비율은 판의 유효 강성과 그에 따른 파장의 속도를 결정한다. 기술 적용에서는 이것에서 쉽게 파생되는 보다 실용적인 매개변수, 즉 두께와 빈도의 산출물을 사용한다.

${\displaystyle f\cdot d={\frac {d\cdot c}{\patchda },}$

모든 파도에 대해서 이래.

$c=f\f\fda.}$

속도와 주파수(또는 파장)의 관계는 특성 방정식에 내재되어 있다. 판의 경우 이러한 방정식은 단순하지 않고 그 해법은 수치적 방법을 필요로 한다. 이것은 램의 원작 이후 40년 만에 디지털 컴퓨터가 등장하기 전까지 난해한 문제였다. 구소련에서 빅토로프가^[4] 컴퓨터로 제작한 「분산곡선」의 출판, 미국의 월튼에 이어 파이어스톤이 출판되었고, 결국 다른 많은 사람들이 람파 이론을 실용성의 영역으로 끌어들였다. 자유 "분산 계산기"(DC)^[5] 소프트웨어는 등방성 판과 다층 비등방성 검체에 대한 분산 도표를 계산할 수 있다. 판에서 관측된 실험 파형은 산포 곡선을 기준으로 해석하면 이해할 수 있다.

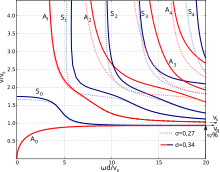
분산 곡선 - 분산 시스템에서 파장 속도, 파장 및 주파수 사이의 관계를 보여주는 그래프 - 다양한 형태로 표시할 수 있다. 기초 물리학에 대한 가장 큰 통찰력을 주는 형태는 y축에 $\Omega {\displaystyle }$ ${\displaystyle \omega }($사각형 주파수)이 있고, x축에는 k(파형 번호)가 있다. 양파를 실용화한 빅토로프가 사용한 형태는 y축에 파동속도를, x축에는 d$/d$ 디스플레이 스타일 d$/\lambda$ $\},$ 두께/파장비를 가진다. 가장 실용적인 형태는 플로이드 파이어스톤 뿐만 아니라 J.와 H. 크라우트크래머에 기인하는 크레디트 형태로서(이것은 우연히 "램파"라는 말을 만들어냈다)는 것은 y축에는 파동속도를, x축에는 주파수 두께 제품인 fd를 가지고 있다.

램의 특성 방정식은 폭 $[\displaystyle d$}의 무한 판에 사인파 모드 두 전체 패밀리의 존재를 나타낸다$.$ 이는 종파와 횡파 또는 전단파, 두 가지 파형 모드만 있는 무한 미디어의 상황과 대조된다. 단일 자유 표면을 따라 전파되는 Rayleigh파에서와 같이, Lamb파에서의 입자 운동은 플레이트 내 깊이에 따라 x와 z 성분으로 타원형이다.^[6] 모드의 한 제품군에서 동작은 중간고사 평면에 대칭이다. 다른 가족에서 그것은 비대칭이다. 속도 분산 현상은 음향파가 플레이트에서 전파될 때 실험적으로 관측 가능한 파형의 다양성을 유도한다. 관측된 파형에서 보이는 변조를 결정하는 것은 위에서 언급한 위상 속도 c 또는 c가_p 아닌 그룹 속도 c이다_g. 파형의 외형은 관찰을 위해 선택한 주파수 범위에 따라 결정적으로 달라진다. 굴곡 모드와 확장 모드는 비교적 쉽게 인식할 수 있으며 이는 비파괴 시험 기법으로서 주장되어 왔다.

제로 오더 모드

대칭 및 대칭 제로 순서 모드는 특별한 주의를 기울여야 한다. 이러한 모드는 "초기 주파수"가 0이다. 따라서 그것들은 0에서 무한정 높은 주파수까지 전체 주파수 스펙트럼에 걸쳐 존재하는 유일한 모드다. 저주파수 범위(즉, 판두께보다 파장이 큰 경우)에서 이러한 모드를 각각 "확장 모드"와 "Flexural 모드"라고 부르는데, 이는 운동의 특성과 전파 속도를 좌우하는 탄성 강성을 설명하는 용어다. 타원 입자 운동은 대칭, 확장 모드용 판 평면에 주로 있으며 대칭, 굴곡 모드용 판 평면에 수직이다. 이러한 특성은 더 높은 주파수에서 변한다.

이 두 모드는 (a) 모든 주파수에서 존재하며 (b) 대부분의 실제 상황에서는 고차 모드보다 더 많은 에너지를 전달하기 때문에 가장 중요하다.

제로오더 대칭모드(지정₀ S)는 저주파수체에서 "플레이트 속도"로 이동하며, 여기서 적절히 "확장모드"라고 부른다. 이 체제에서는 판이 전파 방향으로 뻗어 있고 그에 상응하여 두께 방향으로 수축된다. 주파수가 증가하고 파장이 플레이트 두께와 비교 가능하게 되면서 플레이트의 굴곡은 유효 뻣뻣함에 상당한 영향을 미치기 시작한다. 위상 속도는 완만하게 떨어지는 반면 그룹 속도는 최소한으로 다소 가파르게 떨어진다. 아직 더 높은 주파수에서 위상 속도와 그룹 속도 모두 위로부터의 위상 속도와 아래로부터의 그룹 속도인 Rayleigh 파형 속도로 수렴한다.

확장 모드에 대한 저주파수 한계에서 표면 변위의 z 및 x 성분들은 4각이며 진폭의 비율은 다음과 같다.

${\displaystyle {\frac {a_{z}}{a_{x}}={\frac {\pi \nu }{{(1-\nu )}}}.{\frac {d}{\buffda }}$

여기서 $\nu {\displaystyle }$ ${\displaystyle \nu}$은(는) 포아송의 비율이다$$.

제로오더 대칭모드(지정 A₀)는 "유연모드" 또는 "벤딩모드"라고 적절하게 불리는 저주파수체제에서 분산성이 높다. 매우 낮은 주파수(매우 얇은 판)의 경우 위상 및 그룹 속도는 모두 주파수의 제곱근에 비례하며, 그룹 속도는 위상 속도의 두 배가 된다. 이 단순한 관계는 휨에서 얇은 판에 대한 강성/두께 관계의 결과물이다. 더 이상 파장이 판 두께보다 크지 않은 고주파에서 이러한 관계는 분해된다. 위상 속도는 점점 더 빠르게 상승하고 고주파 한계치에서 레일리파 속도로 수렴한다. 그룹 속도는 파장이 플레이트 두께와 거의 동일한 경우 전단파 속도보다 약간 빠른 최대값을 통과한다. 그런 다음 고주파수 한계치에서 위쪽에서 레일리파 속도로 수렴한다.

확장 모드와 굴곡 모드를 모두 흥분시키고 감지할 수 있는 실험에서, 확장 모드는 종종 굴곡 모드에 대한 더 높은 속도, 더 낮은 전조로 나타난다. 휨모드는 둘 중 더 쉽게 흥분하며 대부분의 에너지를 운반하는 경우가 많다.

고차 모드

주파수가 높아짐에 따라 고차파 모드는 제로오더 모드에 더하여 그 모습을 드러낸다. 각 고차 모드는 플레이트의 공명 주파수에서 "태생"하며, 그 주파수 위에서만 존재한다. 예를 들어, 200kHz 주파수에서 3⁄4 인치(19mm) 두께의 강판, 처음 4개의 램파 모드가 있고 처음 6개인 300kHz가 있다. 처음 몇 개의 고차 모드는 유리한 실험 조건에서 뚜렷하게 관찰할 수 있다. 덜 유리한 조건에서는 그것들은 겹치고 구별할 수 없다.

고차 Lamb 모드는 플레이트 표면과 평행한 플레이트 내의 노달 평면으로 특징지어진다. 이러한 각각의 모드는 그것의 "초점 주파수"라고 불릴 수 있는 특정 주파수 위에만 존재한다. 어떤 모드에도 상한 주파수 제한이 없다. 초기 주파수는 플레이트의 평면에 수직으로 전파되는 세로 또는 전단파에 대한 공명 주파수로 그려질 수 있다.

${\displaystyle d={\frac {n\n\flda }{2}}\reason \text{or}\reason f={\frac}{2d}}}}}$

여기서 n은 양의 정수다. 여기서 c는 종파 속도 또는 전단파 속도 중 하나가 될 수 있으며, 각 결과 공진 세트에 대해 해당 람파 모드는 대칭과 대칭이 번갈아 가며 사용된다. 이 두 세트의 상호작용은 언뜻 보기에 불규칙해 보이는 초기 주파수 패턴을 낳는다. For example, in a 3/4 inch (19mm) thick steel plate having longitudinal and shear velocities of 5890 m/s and 3260 m/s respectively, the nascent frequencies of the antisymmetric modes A₁ and A₂ are 86 kHz and 310 kHz respectively, while the nascent frequencies of the symmetric modes S₁, S₂ and S₃ are 155 kHz, 172 kHz and 343 kHz respectively.

초기 주파수에서 이러한 각 모드는 무한 위상 속도와 그룹 속도를 0으로 한다. 고주파수 한계에서 이러한 모든 모드의 위상 및 그룹 속도는 전단파 속도에 수렴한다. 이러한 수렴성 때문에 두꺼운 판에서는 레일리(Rayleigh)와 전단 속도(서로 매우 가까운 속도)가 크게 중요하다. 간단히 공학적 중요성이 가장 큰 재료로 설명하면, 강판에 장거리를 전파하는 고주파 에너지의 대부분은 3000~3300m/s로 이동한다.

램파 모드에서 입자 운동은 일반적인 타원형이며 플레이트의 평면에 수직이고 평행한 구성요소를 가지고 있다. 이러한 구성 요소는 4각형이다. 즉, 90° 위상 차이를 가진다. 구성 요소의 상대적 크기는 주파수의 함수다. 특정 주파수 두께 제품의 경우, 한 성분의 진폭은 0을 통과하여 움직임이 플레이트의 평면에 완전히 수직 또는 평행하도록 한다. 판 표면에 있는 입자의 경우, 이러한 조건은 양파 위상 속도가 각각 √2c일_t 때 또는 대칭 모드의 경우에만_l 발생한다. 이러한 방향성 고려사항은 플레이트에서 인접 유체로 음향 에너지가 복사되는 것을 고려할 때 중요하다.

입자 운동은 또한 모드의 초기 주파수에서 플레이트의 평면에 완전히 수직이거나 완전히 평행이다. 플레이트의 종파 공진에 해당하는 모드의 초기 주파수에 근접하여, 이들의 입자 운동은 거의 전적으로 플레이트의 평면에 수직이며, 전단파 공진 근처에 평행하게 위치한다.

J.와 H. 크라우트크래머는 양파를 판을 가로질러 적절한 각도로 전파되는 종파와 전단파의 계통으로 생각할 수 있다고^[7] 지적했다. 이러한 파동은 반사되고 모드 전환되며 결합되어 지속적이고 일관성 있는 파동 패턴을 생성한다. 이 일관성 있는 파형 패턴이 형성되려면 판 두께가 기초 종파 및 전단파의 전파각과 파장에 비례하여 정확히 맞아야 한다. 이 요건은 속도 분산 관계로 이어진다.

원통형 대칭이 있는 양파, 점원으로부터의 판파

램의 분석은 직선 파형을 가정했지만, 원통형 판파(즉, 선원에서 바깥쪽으로 전파되는 파동, 판에 수직으로 놓여 있는 선)에는 동일한 특성 방정식이 적용되는 것으로 나타났다^[8]. 차이점은 직선파의 "캐리어"는 사인파인 반면, 축대칭파의 "캐리어"는 베셀 함수라는 것이다. 베셀 함수는 근원의 특이점을 처리한 다음, 먼 거리에서 정현상 행동을 향해 수렴한다.

이러한 원통형 파장은 점 교란에 대한 플레이트의 반응을 구성할 수 있는 고유 기능이다. 따라서 점 교란에 대한 플레이트의 반응은 양파의 조합으로 표현될 수 있으며, 게다가 근거리 영역의 발생적인 용어들을 합친 것이다. 전체적인 결과는 연못에 떨어진 돌에서 나오는 잔물결처럼 원형 파도의 패턴으로 느슨하게 시각화 될 수 있지만 그것들이 바깥쪽으로 진행되면서 형태가 더욱 심오하게 변화한다. 양파 이론은 (r,z) 방향의 움직임에만 관련된다. 가로 방향 운동은 다른 주제다.

유도 양 파동

이 문구는 비파괴시험에서 상당히 자주 접하게 된다. "유도 양파"는 실제 시험 물체의 유한한 치수에 의해 유도되는 양파와 같은 파형으로 정의할 수 있다. "람파"라는 구절에 "안내"라는 접두사를 덧붙이는 것은 따라서 램의 무한판이 실제로는 어디에도 없다는 것을 인식하기 위함이다.

실제로 우리는 유한한 판, 또는 원통형 파이프나 용기로 포장된 판, 또는 얇은 조각으로 자른 판 등을 다룬다. 양파 이론은 종종 그러한 구조물의 파동 행동의 많은 부분을 매우 잘 설명해준다. 완벽한 설명을 해주지 못할 것이고, 그렇기 때문에 '양파 안내'라는 말이 '람파'보다 더 실제적으로 관련이 있는 것이다. 한 가지 의문은 양의 파동의 속도와 모드 모양이 파트의 실제 기하학에 의해 어떻게 영향을 받을 것인가 하는 것이다. 예를 들어 얇은 실린더에서 양처럼 생긴 파동의 속도는 원통의 반지름과 파형이 축을 따라 이동하는지 원주를 따라 이동하는지 여부에 따라 약간 달라진다. 또 다른 질문은 부품의 실제 기하학에서 완전히 다른 음향 동작과 파동 모드가 존재할 수 있는 것이다. 예를 들어 원통형 파이프는 파이프 벽의 Lamb-like 휨 모드와는 상당히 다른 전체 파이프의 신체 이동과 관련된 휨 모드를 가진다.

초음파 검사에서 양파

초음파 테스트의 목적은 일반적으로 테스트 대상 물체의 개별 결함을 찾아 특징짓는 것이다. 이러한 결함은 충돌파를 반사 또는 산란시키고 반사 또는 산란된 파동이 충분한 진폭을 가지고 검색대에 도달했을 때 감지된다.

전통적으로 초음파 검사는 검사 대상 부품의 치수보다 파장이 매우 짧은 파장을 사용해 왔다. 이 고주파-레지타임에서 초음파 검사기는 무한중간 종파 및 전단파 모드에 근접한 파형을 사용하여 판 두께를 가로질러 지그재깅한다. 비록 양파 개척자들이 비파괴 시험 어플리케이션에 대해 연구하여 이 이론에 주의를 끌었지만, 확산 곡선을 계산하고 그것들을 실험적으로 관측 가능한 신호와 관련시키는 컴퓨터 프로그램이 훨씬 더 널리 이용 가능하게 된 1990년대까지는 널리 쓰이지 않았다. 이러한 계산 도구는 양파의 성질에 대한 보다 광범위한 이해와 함께 판 두께와 비교하거나 더 큰 파장을 이용한 비파괴 시험 기법을 고안할 수 있게 했다. 이렇게 긴 파장에서 파장의 감쇠가 적어 더 먼 거리에서 결함을 감지할 수 있다.

초음파 시험에 양파를 사용하는 데 있어 주요한 도전과 기술은 잘 전파되고 깨끗한 리턴 "에코"를 제공하는 특정 주파수에서 특정 모드를 생성하는 것이다. 이것은 세심한 흥분 조절을 필요로 한다. 이를 위한 기법에는 빗 변환기, 웨지, 액체 매체로부터의 파동 및 전자기 음향 변환기(EMAT)의 사용이 포함된다.

초음파 초음파 시험에서의 양파

음향초음파 시험은 결함을 개별적으로 특성화하는 것이 아니라 상당한 영역에 걸쳐 분포된 손상(및 기타 재료 속성)을 평가하는 수단으로 고안되었다는 점에서 초음파 시험과 다르다. 양파는 판 전체 두께를 조사하며 일정한 운동 패턴으로 상당한 거리를 전파하기 때문에 이 개념에 잘 맞는다.

음향 방출 테스트에서의 양파

음향 방출은 기존의 초음파 시험보다 훨씬 낮은 주파수를 사용하며, 센서는 일반적으로 최대 몇 미터 거리에서 활성 결함을 탐지할 것으로 예상된다. 음향 방출을 사용해 시험하는 구조물의 상당 부분은 철판 - 탱크, 압력 용기, 파이프 등 -로 제작된다. 따라서 양파 이론은 음향 방출 시험을 수행할 때 관측되는 신호 형태와 전파 속도를 설명하기 위한 기본 이론이다. AE 소스 위치(AE 테스트의 주요 기술)의 정확도는 양파의 지식 본체를 잘 이해하고 능숙한 활용을 통해 크게 향상될 수 있다.

초음파 및 음향 방출 테스트 대비

플레이트에 임의의 기계적 흥분은 다양한 주파수 범위에서 에너지를 전달하는 다양한 양의 파장을 생성한다. 음향방출파가 그렇다. 음향 방출 테스트에서 과제는 수신된 파형에서 여러 개의 람파 성분을 인식하고 소스 이동 측면에서 해석하는 것이다. 이는 초음파 시험에서 첫 번째 도전은 단일 주파수에서 잘 제어되는 단일 램파 모드를 생성하는 것과 대비된다. 그러나 초음파 시험에서도 발생된 램파가 결함과 상호작용을 할 때 모드 변환이 이루어지기 때문에 다중 모드에서 복합된 반사신호의 해석은 결함특성화 수단이 된다.

참고 항목

• 음향학
• 음향파
• 파동 방정식
• 도파관
• 도파관(음향)
• 도파관(전자기학)

참조

• 로즈, J.L.; 캠브리지 대학 출판부, 1999. "솔리드 미디어의 초음파 파동"

외부 링크

• NDT 자원 센터의 음파 전파 모드
• 비파괴시험 백과사전의 양파장
• 류젠칭에 의한 판내 음향-초음파 신호의 양파 분석 : 완전한 양파 방정식을 포함한 논문