코스니타의 정리

X(54)는 ABC 삼각형의 코스니타 점이다.

유클리드 기하학에서 코시니타의 정리는 임의의 삼각형과 연관된 특정 원의 속성이다.

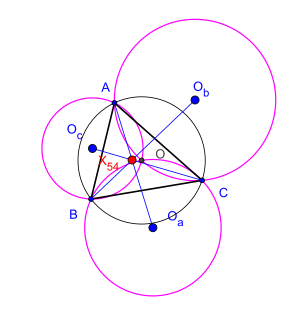
Let ${\displaystyle ABC}$ be an arbitrary triangle, ${\displaystyle O}$ its circumcenter and ${\displaystyle O_{a},O_{b},O_{c}}$ are the circumcenters of three triangles ${\displaystyle OBC}$, ${\displaystyle OCA}$, and ${\displaystyle OAB}$ respectively.정리에서는 A O ${\displaystyle {}_{}}$ ${\$ B ${\displaystyle {}_{}}$ ${\displaystyle b_{}}$ ${\$ C ${\displaystyle O_{}}$ c ${\$의 세 직선이 동시라고$$ 주장한다.^[1]이 결과는 루마니아의 수학자 세자르 코즈니ă(1910-1962)에 의해 확립되었다.^[2]

이들의 일치점은 삼각형의 코시니타 포인트(1997년 리그비명)로 알려져 있다.그것은 9점 중심부의 등각 결합이다.^[3][4]클라크 킴벌링 리스트에 있는$$ 삼각형 중심 $X{\displaystyle }$ ${\displaystyle (54}$) ${\displaystyle$ X $(54)}$이다.^[5]이 정리는 주기적인 육각형과 연관된 6개의 원주에 대한 다오의 정리의 특별한 경우다.^{[6][7][8][9][10][11][12]}

참조