하켄부시

Hackenbush
그루초 마르크스 캐릭터를 위해, 휴고 Z.Hackenbush, A Day at the Races (영화)를 보라.
하켄부시 게임의 시작 설정

해켄부시는 수학자 존 호튼 콘웨이가 개발한 2인용 게임이다.[1]그것은 끝점과 "접지" 라인에 의해 서로 연결된 컬러 선 세그먼트의 모든 구성에서 재생될 수 있다.

게임플레이

게임은 플레이어가 "그라운드" 라인(논문 하단과 다른 플레이 영역의 수평선)을 그리고 각 라인 세그먼트가 엔드포인트에서 직접 연결되거나 또는 엔드포인트에 의해 연결된 다른 세그먼트의 체인을 통해 간접적으로 지면에 연결되는 여러 라인 세그먼트로 시작된다.한 지점에서 임의의 수의 세그먼트가 충족될 수 있으므로 접지 경로가 여러 개일 수 있다.

그들의 차례가 되면, 플레이어는 그들이 선택한 모든 라인 부분을 "컷"(지우기)한다.모든 선 세그먼트는 더 이상 어떤 경로 "낙하"에 의해 지면에 연결되지 않는다(즉, 삭제됨).보통 콤비네이터 게임 이론의 플레이 관례에 따르면, 움직일 수 없는 첫 번째 플레이어가 진다.

해켄부시 보드는 미세하게 많은 ("마인드 보드"의 경우) 또는 무한히 많은 ("무한 보드"의 경우) 라인 세그먼트로 구성될 수 있다.라인 세그먼트의 무한정 수가 존재한다고 해서 그라운드를 직접 "터칭"하는 라인 세그먼트만 미세하게 많다면 유한한 시간 내에 게임을 끝낼 수 있다는 게임 이론 가정에 위배되지 않는다.무한보드에서는 무한히 많은 포인트가 땅에 닿는다고 가정할 때, 보드의 레이아웃에 기초하여 게임은 영원히 계속될 수 있다.

변형

파란 빨간색의 해켄부시 소녀, 수학 연극의 승리 방법이라는 책에서 소개되었다.

하켄부시의 원래 민속 버전에서는 어떤 플레이어도 우위를 점할 수 있다. 이것은 공평한 게임이기 때문에 스프래그-그룬디 정리를 사용하여 완전한 분석을 하는 것은 비교적 간단하다.따라서 결합 게임 이론에 대한 해켄부시 버전의 관심사는 보다 복잡한 당파적 게임이며, 이는 한 플레이어가 같은 포지션으로 이동할 차례라면 한 플레이어가 사용할 수 있는 옵션(모브)이 반드시 다른 플레이어가 사용할 수 있는 것이 아니라는 것을 의미한다.이는 다음 두 가지 방법 중 하나로 달성된다.

  • 오리지널 해켄부시:모든 라인 세그먼트는 같은 색이며 어느 한 선수가 절단할 수 있다.즉, 보수가 대칭이며 각 플레이어는 탑승 위치에 따라 동일한 작업을 수행한다(이 경우 그리기 구조).
  • 파란색-빨간색 해켄부시: 각 선 세그먼트는 빨간색 또는 파란색이다.한 선수(보통 첫 번째 또는 왼쪽, 왼쪽)는 파란색 라인 세그먼트만 절단할 수 있고, 다른 선수(보통 두 번째 또는 오른쪽)는 빨간색 라인 세그먼트만 절단할 수 있다.
  • 블루-레드-그린 해켄부시: 각 라인 세그먼트는 빨강, 파랑 또는 녹색으로 되어 있다.이 규칙은 블루-레드 해켄부시와 동일하며, 그린 라인 세그먼트는 어느 선수라도 자를 수 있다는 추가 규정이 있다.

블루-레드 해켄부시는 블루-레드-그린 해켄부시의 특수한 사례에 불과하지만, 분석이 훨씬 간단한 경우가 많기 때문에 별도로 주목할 필요가 있다.블루-레드 해켄부시는 이른바 콜드게임으로, 본질적으로 첫발을 내딛는 것이 결코 유리할 수 없다는 것을 의미하기 때문이다.

분석

해켄부시는 종종 이 분야의 창시자들이 쓴 '숫자와 게임에 관한 책과 수학 놀이의 이기는 방법'에서 시작하여 결합 게임 이론의 정의와 개념을 보여주는 예시 게임으로 사용되어 왔다.특히 청색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적색-적합성-적합성적-적-적합성적-적-적합성적-적합성적합성적-적합성적합성적합성적합성적합성적합성-적합성적합성블루-레드-그린 해켄부시는 스타와 다른 모든 민첩한 선수와 같이 실제 숫자가 아닌 추가 게임을 만들 수 있다.

게임의 추가 분석은 정점과 가장자리의 집합체로서 보드를 고려하고 지면에 놓여 있는 각 정점에 대한 경로를 조사함으로써 그래프 이론을 사용하여 할 수 있다(그것은 구별되는 정점으로 간주되어야 한다 - 그래프의 선으로 간주하는 것이 아니라 모든 지점을 함께 식별하는 것이 해롭지 않다).

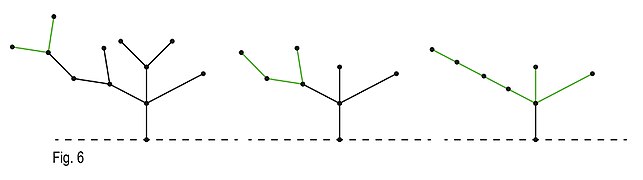
공평한 버전의 하켄부시(플레이어가 특정 색을 사용하지 않는 것)에서는 게임을 수직, 수렴, 다이버전트 등 몇 가지 경우로 나누어 님 힙을 사용하는 것을 생각할 수 있다.대나무 줄기로도 불리는 라인 세그먼트의 수직 스택으로만 플레이되는 이 게임은 님이 직접 되며 이와 같이 직접 분석할 수 있다.다른 부분, 즉 나무는 게임에 주름을 더하고 나뭇가지가 꼭지점에서 모일 때, 가지들을 빠른 총액과 동일한 길이의 비지점 줄기로 교체할 수 있다는 대장 원리의 사용을 요구한다.이 원리는 게임의 표현을 대나무 줄기의 보다 기본적인 버전으로 바꾼다.만들 수 있는 마지막 가능한 그래프 집합은 임의의 뿌리 그래프라고도 알려진 수렴 그래프들이다.퓨전 원리를 사용함으로써 어떤 사이클의 모든 정점이 그래프의 값을 변경하지 않고 함께 융합될 수 있다고 기술할 수 있다.[2]따라서 어떤 수렴 그래프도 단순한 대나무 줄기 그래프로 해석할 수 있다.세 가지 유형의 그래프를 모두 결합하면 게임의 총량을 변경하지 않고도 게임에 복잡성을 더할 수 있어 게임이 님의 전략을 취할 수 있게 된다.

결장 증명 원칙

콜론 원리는 나뭇가지가 꼭지점에서 모일 때, 가지들을 빠른 총액과 같은 길이의 비지점 줄기로 대체할 수 있다고 말한다.고정적이지만 임의의 그래프 G를 고려하고 G에서 임의의 꼭지점, x를 선택한다. H와1 H를2 동일한 Sprague-Grundy 값을 갖는 임의의 트리(또는 그래프)가 되도록 한다.두 개의1 그래프x G = G : H1, G2 = Gx : H를2 고려하십시오. 여기서x Gi : H는 그래프 G의 꼭지점 x에 트리 H를i 부착하여 구성한 그래프를 나타낸다.대장 원리는 두 그래프 G1과 G2가 동일한 Sprague-Grundy 값을 갖는다고 말한다.두 게임의 합계를 그림 5.4와 같이 고려한다.G와1 G가2 같은 스프래그-그룬디 값을 갖고 있다는 주장은 두 경기의 합이 스프래그-그룬디 값 0이라는 주장과 맞먹는다.즉, 합계 G1 + G가2 P 위치라는 것을 보여 주는 것이다.G1+G에서2 두 번째로 움직인 선수라면 승리가 보장된다. 한 경기에서는 첫 번째 선수가 G에서 한 쪽 가장자리를 잘라서 움직이면 두 번째 선수가 다른 경기에서도 G에서 같은 가장자리를 깰 수 있다.(이러한 한 쌍의 움직임으로 H와1 H가2 게임에서 삭제될 수 있지만 그렇지 않으면 H와1 H는2 방해받지 않는다.)만약 첫 번째 플레이어가1 H나 H에서2 가장자리를 잘라 움직인다면, H와12 H의 스프래그-그룬디 값이 더 이상 같지 않기 때문에, 스프래그-그룬디 값을 동일하게 유지하는 움직임이 H나1 H에2 존재한다.이런 식으로 너는 그가 할 수 있는 모든 행동에 대해 항상 회답을 할 것이다.이것은 네가 마지막 수를 써서 이긴다는 것을 의미한다.[3]

  • 콜론 원리를 사용하여 게임을 줄일 수 있는 예

참조

  1. ^ 해켄부시란 무엇인가?geometer.org에서.
  2. ^ R., Berlekamp, Elwyn (2001–2004). Winning ways for your mathematical plays. Conway, John H. (John Horton), Guy, Richard K. (2nd ed.). Natick, Mass.: A.K. Peters. ISBN 9781568811420. OCLC 45102937.
  3. ^ Ferguson, Thomas S. (Fall 2000). "Game Theory" (PDF).

외부 링크