우정 그래프

우정 그래프
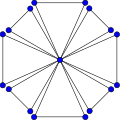우정8 그래프 F.
정점	2n+1
가장자리	3n
반지름	1
지름	2
둘레	3
색수	3
색도 지수	2n
특성.	단위 거리 플라나르 오일러어 요인에 중요한 국소 선형의
표기법	Fn
그래프 및 모수 표

그래프 이론의 수학 분야에서 우정 그래프(또는 네덜란드 풍차 그래프 또는 n-fan) F는_n 2n+1 정점과 3n 가장자리를 갖는 평면 비방향 그래프다.^[1]

우정 그래프 F는_n 주기 그래프 C의₃ n개의 복사본을 공통 꼭지점과 결합하여 구성할 수 있다.^[2]

시공에 의해 우정의 그래프 F는_n 풍차 그래프 Wd(3, n)와 이형이다.둘레 3, 지름 2, 반지름 1의 단위 거리다.그래프 F는₂ 나비 그래프와 이형이다.

우정 정리

폴 에르데스, 알프레드 레니, 베라 T의 우정 정리. 소스(1966)는 ^[3]두 꼭지점마다 정확히 하나의 이웃을 가지고 있는 속성을 가진 유한한 그래프가 정확히 우정 그래프라고 말한다.비공식적으로, 만약 한 무리의 사람들이 모든 한 쌍의 사람들이 정확히 한 명의 친구를 가지고 있다는 재산을 가지고 있다면, 다른 모든 사람들과 친구인 한 사람이 있어야 한다.그러나 무한 그래프의 경우 이 속성을 가진 동일한 카디널리티의 여러 가지 그래프가 있을 수 있다.^[4]

우정의 정리에 대한 조합 증명서는 머르지오스와 운거에 의해 주어졌다.^[5]또 다른 증거는 크레이그 후네케에 의해 주어졌다.^[6]2018년 10월 알렉산더 판 데르 베켄스가 메타트 메일링 리스트에서 메타트에서의 공식화된 증거를 보고하였다.^[7]

라벨링 및 착색

우정 그래프는 색도 번호 3과 색도 지수 2n을 가지고 있다.그것의 색도 다항식은 사이클 그래프 C의₃ 색도 다항식에서 추론할 수 있으며${\displaystyle }$(${\displaystyle \mathrm{x}}$-${\displaystyle {}^{}}$2)${\displaystyle {}^{}{n}^{}}$ (${\displaystyle \mathrm{x}}$ ${\displaystyle -{}^{}}$1 ) ${\displaystyle n^{}}$ ${\displaystyle {}^{}}$($x-2)^{n}(x-1)^{n}x}$와 같다$.$

우정의 그래프_n F는 n이 이상할 경우에만 가장자리-그레이스적이다.n ≡ 0 (mod 4) 또는 n ^[8][9]≡ 1 (mod 4)일 경우에만 우아하다.

모든 우정 그래프는 중요한 요소다.

극단 그래프 이론

극단적 그래프 이론에 따르면 (정점 수에 비례하여) 에지가 충분히 많은 모든 그래프는 하위 $그래프$로 k ${\displaystyle k}$ -fan을$$ 포함해야 한다.보다 구체적으로, 가장자리 수가 다음과 같은 경우 $n{\displaystyle }$ ${\displaystyle n}$ -vertex$$ 그래프에 적용된다.

${\displaystyle \left\lfloor {n^{2}}:{4}\right\floor +f(k),}$

여기서 $f{\displaystyle }$(${\displaystyle k}$) ${\displaystyle f(k)}$은(는) $k{\displaystyle {}^{}}$ 2${\displaystyle {}^{}}$- k ${\displaystyle k}$이(가) 홀수일 경우$$ k ${\displaystyle 2}$ -${\displaystyle {}^{}}$${\displaystyle k}$ ${\displaystyle$ $k^{2}-k}-k}$이며, $k{\displaystyle }$ ${\displaysty k}$이(가) 짝수일 경우$$ f${\displaystyle (}$는 k -${\displaystyle \mathrm{3k}}$$)$이다.이러한 경계는 삼각형이 없는 그래프에서 가장자리 수에 대한 투란의 정리를 일반화하며, $더{\displaystyle }$ 적은 수의 가장자리에는 k ${\displaystyle k}$ -fan을$$ 포함하지 않는 그래프가 존재한다는 점에서 이 문제에 대해 가능한 최선의 경계다.^[10]

참조