프레셰 거리

수학에서, 프레셰 거리(Frechet distance)는 곡선을 따라 점들의 위치와 순서를 고려한 곡선들 사이의 유사성의 측도입니다.그것은 모리스 프레셰의 이름을 따서 지어졌습니다.

직관적 정의

개가 별도의 유한한 곡선 경로를 가로지르며 목줄을 매고 개를 산책시키는 사람을 상상해 보세요.각각은 끈을 늦추기 위해 속도를 바꿀 수 있지만, 둘 다 뒤로 움직일 수 없습니다.두 곡선 사이의 프레셰 거리는 두 곡선이 시작부터 끝까지 별도의 경로를 통과할 수 있는 가장 짧은 끈의 길이입니다.이 정의는 두 곡선에 대해 대칭적입니다. 개가 주인을 산책시키는 경우 프레셰 거리는 동일합니다.

형식 정의

S ${displaystyle$ S $}$ 를 $S$ 메트릭 공간으로 $S$ 합니다.S{displaystyle S}의 곡선 A({displaystyle A})는 단위 간격에서 S{displaystyle S}(즉, A : [0,1] → S{displaystyle A:[0,1]\rightarrow S})로 이어지는 연속적인 지도이다 $le \alpha$ : [ $0,1]\rightarrow [0,1$

A(디스플레이 스타일 A)와 B(디스플레이 스타일 B)를 S(디스플레이 스타일 S)에서 두 개의 곡선으로 지정하고, A(디스플레이 스타일 A)와 B(디스플레이 스타일 B) 사이의 프레셰 거리를 [0, 1]의 전체 재파라미터화 α({displaystyle \alpha})와 β({displaystyle \beta})의 전체 최대 [0, 1]의 최대 디스플레이 스타일 [0, 1]의 최소로 정의한다, $t\in [0,1]$ S에서 $A(\alpha (t))$ ( $(t){\alpha($ $B(\beta (t))$ 와 B $B(\beta (t))$ β $($ ){\ $displaystyle$ B $(\beta(t$ $A(\alpha (t))$ 의 $S$ 에 대한 $\displaystyle$ t $[$ $0$ $S$ ,1 $]}.$ 수학적 표기법에서 프리셰 $F(A,B)$ F $)$ 는 F $(A$ ,B)를 $표시$ 하는 F(A $,B)$ 입니다 $F(A,B)$ $t\in [0,1]$

$\"표시 스타일 F(A,B)=\inf _{\alpha,\big}\,\,\max _{t\in [0,1]}\,\,{\Bigg \}d{\Big(}A(\alpha(t),\beta(t){\Bigg \}}}}$

$d$ 서 d ${displaystyle$ d $}$ 는 $d$ S ${displaystyle$ S $S$ 의 거리 함수입니다.

비공식적으로 $매개변수$ t ${displaystyle$ t $}$ 를 $t$ "시간"으로 생각할 수 있습니다. $A(\alpha (t))$ A $alpha(t))}$ 는 개의 위치이고, $B(\beta (t))$ )){\ $beta$ $(t)}$ 는 $A(\alpha (t))$ $B(\beta (t))$ 개의 $시간$ t $($ 그 반대)에서 개의 주인의 위치입니다. $시간$ t {\ $displaystyle$ $t$ $}$ 에서 $t$ 이들 사이의 끈 길이는 A $A(\alpha (t))$ ( $A(\alpha (t))$ $) (\alpha$ $($ $t))$ 와 $A(\alpha (t))$ $B(\beta (t))$ B $(β$ ( $t$ (\ $A(\alpha (t))$ (t $[0,1]$ 사이의 거리입니다. [ $,$ $]$ 의 $[0,1]$ 가능한 모든 재설정에 대해 $최소값$ 을 취합니다. $}$ 은 $[0,1]$ (는) 최대 리드 길이가 최소화된 지정된 경로를 따라 걷는 것을 선택하는 것에 해당합니다.α ${\displaystyle \alpha$ }와 $\alpha$ $\alpha$ $\beta$ 가 $\beta$ 감소하지 않는다는 $\alpha$ 은 개나 주인 모두가 후퇴할 수 없다는 것을 의미합니다.

프레셰 미터법은 거리가 프레셰 거리에 기여하는 점 쌍이 각각의 곡선을 따라 연속적으로 스위프하기 때문에 두 곡선의 흐름을 고려합니다.따라서 프리셰 거리는 임의의 점 집합에 대한 하우스도르프 거리와 같은 대안보다 곡선에 대한 유사성을 더 잘 측정할 수 있습니다.두 곡선은 하우스도르프 거리는 작지만 프레셰 거리는 클 수 있습니다.

프레셰 거리와 그 변형은 형태^[1] 형성 및 필기 인식에서^[2] 단백질 구조 ^[3]정렬에 이르기까지 여러 문제에서 적용됩니다.Alt와 Godau는^[4] 파라메트릭 검색 원리에 기초하여 유클리드 공간에서 두 다각형 곡선 사이의 프레셰 거리를 계산하는 다항식 시간 알고리즘을 처음으로 설명했습니다.이 알고리즘의 실행 시간은 m과 n 세그먼트가 있는 두 개의 다각형 곡선에 대해 O $O(mn\cdot \log(mn))$ log $O(mn\cdot \log(mn))$ ( $O(mn\cdot \log(mn))$ ) $\$ $displaystyle$ O $(mn\cdot \log(mn))$ 입니다 $O(mn\cdot \log(mn))$ .

자유 공간 다이어그램

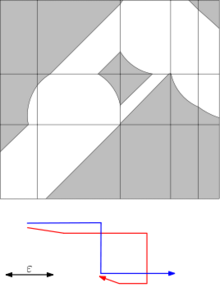
example of a free-space diagram — 빨간색과 파란색 곡선의 자유 공간 다이어그램입니다.두 곡선 모두에 매개변수 간격 [0,1]을 사용하는 텍스트의 정의와 달리 이 예에서는 곡선이 호 길이로 매개변수화됩니다.

두 곡선의 프레셰 거리를 계산하는 중요한 도구는 Alt와 Godau에 ^[4]의해 도입된 자유 공간 다이어그램입니다.주어진 거리 임계값 ε에 대한 두 곡선 사이의 자유 공간 다이어그램은 매개변수 공간에서 최대 ε 거리에 있는 두 곡선의 모든 점 쌍으로 구성된 2차원 영역입니다.

$디스플레이 스타일 D_{\varepsilon}(A,B):=\{\,(\alpha,\beta )\in [0,1]^{2}\midd(A(\alpha),B(\beta))\leq \varepsilon \,\}$

자유 공간 $D_{\varepsilon }(A,B)$ $D_{\varepsilon }(A,B)$ ( $)$ \ $displaystyle D_{\varepsilon}(A, B)}$ 에 $D_{\varepsilon }(A,B)$ 수평 방향과 수직 방향 모두에서 단조로운 경로가 포함된 경우에만 F $A$ , $)$ \ $displaystyle F(A$ , $B)$ 는 $F(A,B)$ 최대 ε입니다.

확률 분포 사이의 거리(FID 점수)

곡선 사이의 거리를 측정하는 것 외에도, Frechet 거리는 확률 분포 간의 차이를 측정하는 데 사용될 수 있습니다.

$\mu _{X}$ $\mu _{X}$ X $({$ $\mu _{Y}$ $\mu _{Y}$ Y $({$ 와 $\mu _{Y}$ 공분산 행렬 $\Sigma _{X}$ X({\ $displaystyle \Sigma_{X})$ 및 $\Sigma _{X}$ $({$ 를 갖는 두 다변량 가우스 분포의 경우 이러한 분포^[5] 사이의 프레셰 거리는 다음과 같습니다.

$d^{2}=|\mu _{X}-\mu _{Y}|^{2}+\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})$ 2 $=$ $d^{2}=|\mu _{X}-\mu _{Y}|^{2}+\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})$ X - $d^{2}=|\mu _{X}-\mu _{Y}|^{2}+\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})$ $d^{2}=|\mu _{X}-\mu _{Y}|^{2}+\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})$ + $d^{2}=|\mu _{X}-\mu _{Y}|^{2}+\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})$ (Δ $d^{2}=|\mu _{X}-\mu _{Y}|^{2}+\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})$ X $d^{2}=|\mu _{X}-\mu _{Y}|^{2}+\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})$ + $d^{2}=|\mu _{X}-\mu _{Y}|^{2}+\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})$ Y - $d^{2}=|\mu _{X}-\mu _{Y}|^{2}+\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})$ ( $d^{2}=|\mu _{X}-\mu _{Y}|^{2}+\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})$ X $d^{2}=|\mu _{X}-\mu _{Y}|^{2}+\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})$ Y ) $d^{2}=|\mu _{X}-\mu _{Y}|^{2}+\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})$ / $d^{2}=|\mu _{X}-\mu _{Y}|^{2}+\operatorname {tr} (\Sigma _{X}+\Sigma _{Y}-2(\Sigma _{X}\Sigma _{Y})^{1/2})$ ) ${\displaystyle$ d $^{2}=$ \ $mu$ _{ $X}-\mu$ _{Y $}$ ^{ $2}$ +\ $Sigma _{Y} _$ { $X}+\Sigma$ _{Y} _{ $1$ _{X} _{X} \X}_{X}_{X}_{MA}_{X}_2}_{X}_{ $MA$ }

이 거리는 생성적 적대 네트워크에 의해 생성된 이미지와 훈련에 사용된 실제 이미지를 비교하는 데 사용되는 FID(Fréchet inception distance)의 기본입니다.

변종

약한 프레셰 거리는 엔드포인트가 각각의 곡선을 따라 단조롭게 움직일 필요 없이 고전적인 프레셰 거리의 변형입니다. 개와 주인은 개 사이의 끈을 짧게 유지하기 위해 역추적할 수 있습니다.Alt와 Godau는^[4] 관련 그리드 그래프의 미니맥스 경로 계산을 기반으로 다각형 곡선 사이의 약한 프레셰 거리를 계산하는 더 간단한 알고리듬을 설명합니다.

결합 거리라고도 하는 이산 프레셰 거리는 아이터와 ^[6]만닐라에 의해 정의된 다각형 곡선에 대한 프레셰 메트릭의 근사치입니다.이산 프레셰 거리는 끝이 두 다각형 곡선의 정점에 위치하고 가장자리 내부에 있지 않는 리드의 위치만 고려합니다.이 특별한 구조를 통해 이산 프레셰 거리는 쉬운 동적 프로그래밍 알고리즘에 의해 다항 시간 내에 계산될 수 있습니다.

두 곡선이 다면체 지형이나 장애물이 있는 일부 유클리드 공간과 같은 유클리드 공간이 아닌 메트릭 공간에 포함될 때 곡선의 두 점 사이의 거리는 가장 자연스럽게 두 점 사이의 최단 경로 길이로 정의됩니다.리드는 엔드포인트에 연결되는 측지선이어야 합니다.곡선 사이의 결과 메트릭을 측지선 프레셰 ^[1]^[7]^[8]거리라고 합니다.쿡과 웬크는^[7] 단순 폴리곤에서 두 다각형 곡선 사이의 측지선 프레셰 거리를 계산하는 다항식 시간 알고리즘을 설명합니다.

만약 우리가 주변 미터법 공간에서 줄이 계속해서 움직여야 한다고 추가로 요구한다면, 우리는 두 곡선 사이의 동형 프레셰^[9] 거리의 개념을 얻습니다.목줄은 한 위치에서 다른 위치로 연속적으로 전환될 수 없습니다. 특히, 목줄은 장애물을 뛰어넘을 수 없으며, 충분히 길어야만 지형에서 산을 쓸 수 있습니다.목줄의 움직임은 두 곡선 사이의 호모토피를 설명합니다.Chambers 등은 장애물이 있는 유클리드 평면에서 다각형 곡선 사이의 동형 프레셰 거리를 계산하는 다항식 시간 알고리듬을 설명합니다.^[9]

예

반경 r1({displaystyle r_{1})과 r2({displaystyle r_{2})의 두 동심원 사이의 프레셰 거리는 각각 r1 - r2이다. {{displaystyle r_{1}-r_{2}}. 주인이 가만히 서 있고 개가 원의 반대쪽으로 이동할 때 가장 긴 끈이 필요하다,주인과 개가 원 주위를 일정한 각속도로 걸을 때 가장 짧은 끈을 묶습니다. ( $|r_{1}-r_{2}|$ - $|r_{1}-r_{2}|$ \ $displaystyle r_{1}-r_{2})$

적용들

프레셰 거리는 그래픽 디자인 ^[10]원리인 시각적 계층 구조를 연구하는 데 사용되어 왔습니다.

참고 항목

레퍼런스

^ ^a ^b Efrat, Alon; Guibas, Leonidas J.; Har-Peled, Sariel; Mitchell, Joseph S. B.; Murali, T. M. (2002), "New similarity measures between polylines with applications to morphing and polygon sweeping" (PDF), Discrete and Computational Geometry, 28 (4): 535–569, doi:10.1007/s00454-002-2886-1, S2CID 16382161.
^ Sriraghavendra, R.; Karthik, K.; Bhattacharyya, Chiranjib (2007), "Fréchet distance based approach for searching online handwritten documents", Proc. 9th International Conference on Document Analysis and Recognition (ICDAR '07), pp. 461–465, doi:10.1109/ICDAR.2007.121, S2CID 2533396.
^ Minghui, Jiang; Ying, Xu; Binhai, Zhu (2008), "Protein structure-structure alignment with discrete Fréchet distance" (PDF), Journal of Bioinformatics and Computational Biology, 6 (1): 51–64, doi:10.1142/S0219720008003278, PMID 18324745.
^ ^a ^b ^c Alt, Helmut; Godau, Michael (1995), "Computing the Fréchet distance between two polygonal curves" (PDF), International Journal of Computational Geometry and Applications, 5 (1–2): 75–91, doi:10.1142/S0218195995000064.
^ Dowson, D. C; Landau, B. V (1 September 1982). "The Fréchet distance between multivariate normal distributions". Journal of Multivariate Analysis. 12 (3): 450–455. doi:10.1016/0047-259X(82)90077-X. ISSN 0047-259X.
^ Eiter, Thomas; Mannila, Heikki (1994), Computing discrete Fréchet distance (PDF), Tech. Report CD-TR 94/64, Christian Doppler Laboratory for Expert Systems, TU Vienna, Austria.
^ ^a ^b Cook, Atlas F., IV; Wenk, Carola (2008), Geodesic Fréchet distance with polygonal obstacles (PDF), Tech. Report CS-TR-2008-0010, University of Texas at San Antonio{{citation}}CS1 유지보수: 여러 이름: 작성자 목록(링크).
^ Maheshwari, Anil; Yi, Jiehua (2005), "On computing Fréchet distance of two paths on a convex polyhedron", Proc. 21st European Workshop on Computational Geometry (PDF), pp. 41–44.
^ ^a ^b Chambers, Erin Wolf; Colin de Verdière, Éric; Erickson, Jeff; Lazard, Sylvain; Lazarus, Francis; Thite, Shripad (2009), "Homotopic Fréchet distance between curves, or Walking your dog in the woods in polynomial time" (PDF), Computational Geometry: Theory and Applications, 43 (3): 295–311, doi:10.1016/j.comgeo.2009.02.008.
^ Urano, Yoko; Kurosu, Aaron; Henselman-Petrusek, Gregory; Todorov, Alexander (2021). "Visual hierarchy relates to impressions of good design". CHI'21 Workshop on Eye Movements as an Interface to Cognitive State: 1–9. doi:10.31234/osf.io/hksf9. S2CID 236599584.

진일보한 내용

de Berg, Mark, "Analyzing Trajectories of Moving Objects", Computational Geometry, Two Selected Topics (PDF), pp. 11–75.
Aronov, Boris, Har-Peled, Sariel, Knauer, Knauer, Knauer, Wang, Yusu, Wenk, Carola (2006), "곡선에 대한 프레셰 거리, 재검토", Proc. 제14회 알고리즘에 대한 유럽 심포지엄(PDF), 컴퓨터 과학 강의 노트, vol. 4168, Springer-Ver-Lag, pp.52-63, Arxiv:150.07.085, 10.10.10.10.10.10.8.1.1.1.8.1.1.1,2010-06-12에 원본(PDF)에서 보관.
Alt, Helmut; Buchin, Maike (2010), "Can we compute the similarity between surfaces?", Discrete and Computational Geometry, 43: 78–99, arXiv:cs.CG/0703011, doi:10.1007/s00454-009-9152-8, S2CID 5799576.

[efrat02new-1] Efrat, Alon; Guibas, Leonidas J.; Har-Peled, Sariel; Mitchell, Joseph S. B.; Murali, T. M. (2002), "New similarity measures between polylines with applications to morphing and polygon sweeping" (PDF), Discrete and Computational Geometry, 28 (4): 535–569, doi:10.1007/s00454-002-2886-1, S2CID 16382161.

[sri07frechet-2] Sriraghavendra, R.; Karthik, K.; Bhattacharyya, Chiranjib (2007), "Fréchet distance based approach for searching online handwritten documents", Proc. 9th International Conference on Document Analysis and Recognition (ICDAR '07), pp. 461–465, doi:10.1109/ICDAR.2007.121, S2CID 2533396.

[minghui08protein-3] Minghui, Jiang; Ying, Xu; Binhai, Zhu (2008), "Protein structure-structure alignment with discrete Fréchet distance" (PDF), Journal of Bioinformatics and Computational Biology, 6 (1): 51–64, doi:10.1142/S0219720008003278, PMID 18324745.

[alt95frechet-4] Alt, Helmut; Godau, Michael (1995), "Computing the Fréchet distance between two polygonal curves" (PDF), International Journal of Computational Geometry and Applications, 5 (1–2): 75–91, doi:10.1142/S0218195995000064.

[gaussian-5] Dowson, D. C; Landau, B. V (1 September 1982). "The Fréchet distance between multivariate normal distributions". Journal of Multivariate Analysis. 12 (3): 450–455. doi:10.1016/0047-259X(82)90077-X. ISSN 0047-259X.

[eiter94discrete-6] Eiter, Thomas; Mannila, Heikki (1994), Computing discrete Fréchet distance (PDF), Tech. Report CD-TR 94/64, Christian Doppler Laboratory for Expert Systems, TU Vienna, Austria.

[cook08geodesic-7] Cook, Atlas F., IV; Wenk, Carola (2008), Geodesic Fréchet distance with polygonal obstacles (PDF), Tech. Report CS-TR-2008-0010, University of Texas at San Antonio{{citation}}CS1 유지보수: 여러 이름: 작성자 목록(링크).

[maheshwari05frechet-8] Maheshwari, Anil; Yi, Jiehua (2005), "On computing Fréchet distance of two paths on a convex polyhedron", Proc. 21st European Workshop on Computational Geometry (PDF), pp. 41–44.

[chambers09homotopic-9] Chambers, Erin Wolf; Colin de Verdière, Éric; Erickson, Jeff; Lazard, Sylvain; Lazarus, Francis; Thite, Shripad (2009), "Homotopic Fréchet distance between curves, or Walking your dog in the woods in polynomial time" (PDF), Computational Geometry: Theory and Applications, 43 (3): 295–311, doi:10.1016/j.comgeo.2009.02.008.

[10] Urano, Yoko; Kurosu, Aaron; Henselman-Petrusek, Gregory; Todorov, Alexander (2021). "Visual hierarchy relates to impressions of good design". CHI'21 Workshop on Eye Movements as an Interface to Cognitive State: 1–9. doi:10.31234/osf.io/hksf9. S2CID 236599584.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

Search