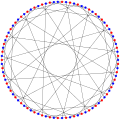
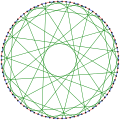
포스터 그래프

Foster graph
포스터 그래프
Foster graph.svg
포스터 그래프
이름을 따서 명명됨로널드 마틴 포스터
정점90
가장자리135
반지름8
지름8
둘레10
자동형성4320
색수2
색도 지수3
대기열 번호2
특성.큐빅
양립자
대칭
해밀턴어
거리-변환
그래프 및 모수 표

그래프 이론의 수학적 분야에서 포스터 그래프는 90 정점과 135개의 가장자리를 가진 초당적 3정형 그래프다.[1]

포스터 그래프는 해밀턴식이며 색도 번호 2, 색도 지수 3, 반지름 8, 지름 8, 둘레 10을 가지고 있다.또한 3-Vertex 연결, 3-edge 연결 그래프이기도 하다.2번 대기열이 있고 책 두께의 상한은 4번이다.[2]

세제곱 거리-정규 그래프는 모두 알려져 있다.[3]포스터 그래프는 13개의 그래프 중 하나이다.교차로 배열 {3,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,2,2,3}[4]이(가) 있는 고유한 거리 변환 그래프다.일반화 쿼드랑글 GQ(2,2)의 8-gon이 없는 독특한 트리플 커버인 부분 선형 공간의 발생 그래프로 구성할 수 있다.그것은 R. M. 포스터의 이름에서 따온 것인데, 포스터의 세제곱 대칭 그래프의 인구 조사에는 이 그래프가 포함되어 있었다.

포스터 그래프의 초당적 절반은 거리 정규 그래프와 국소 선형 그래프다.도표 6을 가진 그러한 그래프의 유한한 수 중 하나이다.[5]

대수적 특성

포스터 그래프의 자동형성 그룹은 순서 4320의 그룹이다.[6]그것은 정점, 가장자리, 그리고 그래프의 호에서 전이적으로 작용한다.따라서 포스터 그래프는 대칭 그래프다.그것은 어떤 정점과 어떤 가장자리로도 가져가는 자동모형을 가지고 있다.포스터 인구조사에 따르면 F90A로 참조되는 포스터 그래프는 90 정점에 대한 유일한 입방 대칭 그래프다.[7]

The characteristic polynomial of the Foster graph is equal to .

갤러리

  • 다양한 사이클을 강조하기 위한 포스터 그래프 색상.

  • 포스터 그래프의 색상은 2이다.

  • 포스터 그래프의 색지수는 3이다.

참조

  1. ^ Weisstein, Eric W. "Foster Graph". MathWorld.
  2. ^ Wolz, Jessica; SAT를 이용한 엔지니어링 선형 레이아웃.2018년 튀빙겐 대학교 석사 논문
  3. ^ 브루워 A. E., 코헨 A. M., 노이마이어 A.거리-일반 그래프.뉴욕: 스프링거-베를라크, 1989.
  4. ^ 세제곱 거리 정규 그래프, A. 브루어.
  5. ^ Hiraki, Akira; Nomura, Kazumasa; Suzuki, Hiroshi (2000), "Distance-regular graphs of valency 6 and ", Journal of Algebraic Combinatorics, 11 (2): 101–134, doi:10.1023/A:1008776031839, MR 1761910
  6. ^ 로일, G. F090A 데이터[permanent dead link]
  7. ^ 콘더, M., 도브사니, P. "삼각형 대칭 그래프 최대 768정점까지." J. 콤빈수학. 콤빈.계산하다.40, 41-63, 2002.
  • Biggs, N. L.; Boshier, A. G.; Shawe-Taylor, J. (1986), "Cubic distance-regular graphs", Journal of the London Mathematical Society, 33 (3): 385–394, doi:10.1112/jlms/s2-33.3.385, MR 0850954.
  • Van Dam, Edwin R.; Haemers, Willem H. (2002), "Spectral characterizations of some distance-regular graphs", Journal of Algebraic Combinatorics, 15 (2): 189–202, doi:10.1023/A:1013847004932, MR 1887234.
  • Van Maldeghem, Hendrik (2002), "Ten exceptional geometries from trivalent distance regular graphs", Annals of Combinatorics, 6 (2): 209–228, doi:10.1007/PL00012587, MR 1955521.