불확실성 포함 예상값

의사결정 이론과 양적 정책 분석에서 불확실성 포함(EVIU)의 기대값은 확률론적 분석에 기초한 결정 대 불확실성을 무시한 분석에 기초한 결정의 예상 가치 차이다.^[1][2][3]

배경

언제 어디서나 불확실성이 존재하는 곳에서 매일 결정을 내려야 한다.대부분의 일상적인 결정에서 다양한 휴리스틱스는 불확실성 앞에서 합리적으로 행동하기 위해 사용되며, 종종 불확실성의 존재에 대해 거의 생각하지 않는다.그러나 공공성이 높은 상황에서 더 큰 고득점 결정이나 결정의 경우, 의사결정자는 종종 양적 분석이나 의사결정 분석과 같이 의사결정 문제에 대한 보다 체계적인 처리로부터 이익을 얻을 수 있다.

정량적 의사결정 모델을 구축할 때, 모델 구축자는 다양한 관련 요소를 식별하고, 이를 입력 변수로 인코딩한다.이러한 투입변수로부터 결과 변수라고 불리는 다른 수량을 계산할 수 있으며, 이는 의사결정자에게 정보를 제공한다.예를 들어, 아래에 상세히 기술된 예에서, 의사결정자는 비행기의 일정 출발 전에 공항으로 출발해야 하는 시간(결정)을 결정해야 한다.한 가지 입력 변수는 공항 주차장까지 운전하는 데 걸리는 시간이다.모델은 이것과 다른 입력정보를 통해 의사결정자가 비행을 놓칠 가능성이 얼마나 되는지와 다양한 의사결정에 대한 순비용(분 단위)을 계산할 수 있다.

결정에 도달하기 위해, 매우 일반적인 관행은 불확실성을 무시하는 것이다.각 입력 변수에 대한 최선의 추측(단일 값)을 사용함으로써 정량적 분석과 모델 구축을 통해 의사결정이 이루어진다.그런 다음 계산된 포인트 추정치에 대해 결정을 내린다.그러나 많은 경우에 불확실성을 무시하면 결과 변수에 대한 추정은 종종 의사결정자를^[4] 오도하는 매우 나쁜 결정을 초래할 수 있다.

정량적 의사결정 모델의 불확실성을 무시하는 대안은 불확실성을 모델의 일부로 명시적으로 인코딩하는 것이다.이 접근방식으로, 각 입력 변수에 대해 하나의 최선의 추측이 아닌 확률 분포를 제공한다.그 분포의 분산은 입력량에서 주관적인 불확실성(또는 지식의 부족)의 정도를 반영한다.그런 다음 소프트웨어 도구는 몬테카를로 분석과 같은 방법을 사용하여 불확실성을 결과 변수에 전파하여 의사결정자가 자신의 결정에 미치는 영향을 명시적으로 파악하며, 많은 경우 결과적으로 훨씬 더 나은 결정을 내릴 수 있다.

불확실성 무시 대 명시적으로 불확실성을 모델링하는 두 가지 접근방식을 비교할 때, 자연스러운 질문은 그것이 도달한 결정의 질에 실제로 얼마나 많은 차이를 만들어 내느냐 하는 것이다.1960년대에 로날드 A. 하워드는 그러한 척도 중 하나인 완벽한 정보의 기대 가치(EVPI)를 제안했는데^[5], 이는 불확실한 모든 입력 변수에 대한 "진정한" 값을 얼마나 학습할 가치가 있는지에 대한 척도였다.불확실성에 대한 민감도에 대한 매우 유용한 측정치를 제공하는 한편, EVPI는 불확실성에 대한 명시적 표현과 추론에서 얻은 결정의 실제 개선을 직접적으로 포착하지 않는다.이를 위해 맥스 헨리온은 박사 논문에서 이 기사의 주제인 불확실성 포함(EVIU)의 기대치를 소개했다.

공식화

내버려두다

${\displaystyle {\begin{array}{ll}d\in D&{\text{the decision being made, chosen from space }}D\\x\in X&{\text{the uncertain quantity, with true value in space }}X\\U(d,x)&{\text{the utility function}}\\f(x)&{\text{the prior subjective probability distribution (density function) on }}x\end{array}}}$

불확실성을 포함하지 않을 경우 불확실한 수량의 예상 값인$$$E{\displaystyle }$[ ${\displaystyle x}$ ${\displaystyle ]}$ ${\displaystyle E[x]}$만 사용하여 최적의 결정을 찾는다.따라서 불확실성을 무시한 결정은 다음과 같은 방법으로 결정된다.

${\displaystyle d_{iu}={\arg \max_{d}~U(d,E[x])).}$

불확실성을 고려한 최적의 결정은 기대 효용성을 최대화하는 베이즈 표준 결정이다.

${\displaystyle d^{*}={\arg \max_{d}{d}{d}}{\int U(d,x)f(x)\,dx}.}$

EVIU는 다음과 같은 두 가지 결정 간의 기대 효용성의 차이다.

${\displaystyle EVIU=\int _{X}\왼쪽[U(d^{*}x)-U(d_{iu}x)\right]f(x)\,dx.}$

불확실한 수량 x와 결정 변수 d는 각각 많은 스칼라 변수로 구성될 수 있으며, 이 경우 공간 X와 D는 각각 벡터 공간이다.

예

오른쪽 도표는 의사결정자가 공항에서 비행기를 타기 위해 얼마나 일찍 집을 떠나야 하는지를 결정하는 영향력 도표다.녹색 사각형의 단일 결정은 비행기의 출발 시간 전에 출발하기로 결정한 시간(분)이다.청록색 난자에서 다이어그램에 4개의 불확실한 변수가 표시됨:집에서 공항 주차장까지 차로 이동하는 데 필요한 시간(분), 주차장에서 게이트까지 가는 데 걸리는 시간(분), 출발 전 탑승구에 있어야 하는 시간(분), 비행기를 놓쳤을 때 발생하는 손실(분) 등이다.이러한 각 노드에는 확률 분포 viz가 포함되어 있다.

Time_to_drive_to_airport   := LogNormal(median:60,gsdev:1.3) Time_from_parking_to_gate  := LogNormal(median:10,gsdev:1.3) Gate_time_before_departure := Triangular(min:20,mode:30,max:40) Loss_if_miss_the_plane     := LogNormal(median:400,stddev:100)

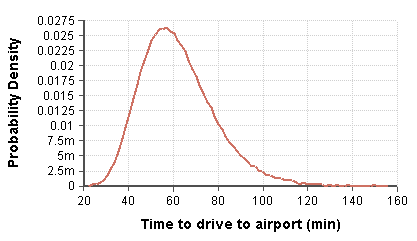
이러한 분포는 각각 통계적으로 독립적인 것으로 간주된다.중위수 60과 기하학적 표준 편차가 1.3인 첫 번째 불확실한 변수 Time_to_drive_to_airport에 대한 확률 분포는 이 그래프에 설명되어 있다.

모델은 비용(빨간색 육각형 변수)을 평면에 성공적으로 탑승하기 위해 소비된 분(또는 분 단위 등가)으로 계산한다.너무 늦게 도착하면 비행기를 놓쳐 다음 비행기를 기다려야 하는 큰 손실(부정적 효용)을 입게 된다.너무 일찍 도착하면 불필요하게 장시간 비행기를 기다려야 하는 비용이 발생한다.

EVIU를 이용하는 모델은 효용 함수를 사용하거나 동등하게 손실 함수를 이용할 수 있다. 이 경우 효용 함수는 손실 함수의 음수일 뿐이다.어느 경우든 EVIU는 긍정적일 것이다.주된 차이점은 단지 손실 함수를 가지고 효용을 극대화하기 보다는 손실을 최소화함으로써 결정을 내린다는 것이다.여기서의 예는 손실 함수인 코스트(Cost)를 사용한다.

따라서 계산된 각 변수에 대한 정의는 다음과 같다.

Time_from_home_to_gate := Time_to_drive_to_airport + Time_from_parking_to_gate + Loss_iff_miss_plane Value_per_at_at_home := 1

비용 := Value_per_minute_at_home * Time_I_leave_home + (If Time_)I_leave_home < Time_from_home_to_gate 그 다음 Loss_if_miss_theplane Ether 0)

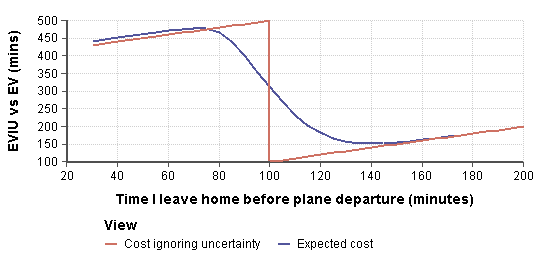
다음 그래프는 불확실성을 무시한 기대 효용에 대한 불확실성을 고려한 기대값(매끄러운 파란색 곡선)을 표시하며, 의사결정 변수의 함수로 그래프로 표시한다.

불확실성이 무시되면 최소 비행 100분 전에 출발하는 한 확실하게 비행이 이뤄지는 것처럼 행동하고, 그보다 더 늦게 출발하면 확실하게 비행을 놓치게 된다.모든 것이 확실한 것처럼 행동하기 때문에 비행 100분(혹은 100분 1초) 전에 정확히 출발하는 것이 최적의 행동이다.

불확실성을 고려할 때 기대값은 매끄럽게(파란 곡선) 되며, 최적 조치는 비행 140분 전에 떠나는 것이다.비행 100분 전 결정으로 기댓값 곡선은 불확실성을 무시할 때 예상되는 비용이 313.7분인 반면, 비행 140분 전 출발할 때 예상되는 비용은 151분이다.이 두 가지 차이점은 EVIU이다.

$[\displaystyle EVIU=313.7-151=162.7]{\text{분}}}$

즉, 결정을 내릴 때 불확실성을 명시적으로 고려한다면 평균 162.7분의 절약이 실현된다.

선형 2차 제어

중앙집중식 선형 2차 제어의 맥락에서, 진화 방정식에는 부가적인 불확실성이 있지만 그 방정식의 계수 값에 대한 불확실성이 없는 상황에서, 불확실성을 고려하는 제어 변수에 대한 최적 솔루션은 불확실성을 무시하는 해결책과 동일하다.불확실성을 포함하는 0의 기대값을 제공하는 이 속성을 확실성 등가성이라고 한다.

완벽한 정보의 기대 가치(EVPI)와의 관계

EVIU와 EVPI 모두 베이지스 결정의 예상 가치를 불확실성 없이 이루어진 또 다른 결정과 비교한다.EVIU의 경우, 불확실성이 존재하지만, EVPI의 경우, 이 다른 결정은 x에 대한 완벽한 정보를 얻음으로써 불확실성이 제거된 후에 이루어진다.

EVPI는 x에 대해 불확실한 예상 비용이고 EVIU는 확실하다고 가정하는 추가 예상 비용이다.

EVIU는 EVPI와 마찬가지로 효용 함수의 단위 측면에서 기대값을 제공한다.

참고 항목

• 샘플 정보의 기대값
• 대량 디스패치 소멸

참조