고갈 지역

반도체 물리학에서 고갈층, 고갈 영역, 접합 영역, 공간 전하 영역 또는 공간 전하층으로도 불리는 고갈 영역은 이동 전하 캐리어가 확산되거나 전계에 의해 제거된 전도성 도프된 반도체 재료 내의 절연 영역입니다.고갈 영역에 남아 있는 유일한 요소는 이온화된 공여체 또는 수용체 불순물입니다.

양이온과 음이온으로 이루어진 이 영역을 이 영역의 캐리어가 고갈되기 때문에 고갈 영역이라고 합니다.

고갈 영역은 모든 자유 전하 캐리어를 제거하여 전도 영역에서 형성되며 전류를 흐르게 하는 영역이 없기 때문에 이러한 이름이 붙습니다.고갈 영역을 이해하는 것은 현대 반도체 전자 장치를 설명하기 위한 핵심입니다. 다이오드, 양극 접합 트랜지스터, 전계 효과 트랜지스터 및 가변 캐패시턴스 다이오드는 모두 고갈 영역 현상에 의존합니다.

p-n 접합부의 형성

그림 1.상단: 확산 전 p-n 접합부; 하단:균형에 도달한 후

그림 2위에서 아래로상단: 접합부를 통한 홀 및 전자 농도; 두 번째: 전하 밀도;세 번째: 전계; 바닥: 전위

그림 3전방 바이어스 모드의 PN 접점은 고갈 폭이 감소합니다.p접합부와 n접합부는 모두 1e15/cm3 도핑 수준에서 도핑되어 약 0.59V의 내장 전위가 발생한다.n 및 p 영역(빨간색 곡선)에서 전도 대역 및 원자가 대역에 대한 서로 다른 준 페르미 수준을 관찰합니다.

고갈 영역은 p-n 접합부에 걸쳐 즉각적으로 형성된다.접점이 열평형 상태이거나 안정된 상태일 때 가장 쉽게 설명됩니다. 두 경우 모두 시스템의 특성은 시간에 따라 달라지지 않으며 동적 ^[1]^[2]평형이라고 불립니다.

전자와 구멍은 잉크가 균등하게 분배될 때까지 물로 확산되는 것처럼 농도가 낮은 영역으로 확산됩니다.정의상 N형 반도체는 P형 반도체에 비해 자유전자(전도대역 내)가, P형은 N형보다 홀(원자가대역 내)이 많다.따라서 N도프 및 P도프 반도체를 함께 배치하여 접합부를 형성하면 N측 전도대역의 자유전자가 P측 전도대역으로 이동(확산)하고 P측 원자가대역의 구멍이 N측 원자가대로 이동한다.

전사에 이어 확산된 전자가 구멍에 접촉해 P측의 재결합에 의해 제거된다.마찬가지로 확산된 구멍은 자유전자와 재결합되어 N측에서 제거된다.최종 결과는 확산된 전자와 구멍이 사라졌다는 것입니다.접합계면 근방의 N측 영역에서는 (1) P측으로의 전자의 확산 및 (2) P측에서 확산되는 구멍으로의 전자의 재결합에 의해 전도대역의 자유전자가 없어진다.인터페이스 근처의 P측 영역에 있는 구멍도 같은 이유로 없어집니다.그 결과 접합계면 주변에서는 다수전하 캐리어(N형 반도체에서는 자유전자, P형 반도체에서는 홀)가 고갈되어 이 영역을 고갈 영역 또는 고갈 영역이라고 한다.상기 과전하 캐리어 확산에 의해 공핍영역이 대전되어 그 N측이 정전하되고 P측이 음전하된다.그러면 전하 확산에 반대되는 힘을 제공하는 전장이 생성됩니다.전기장이 구멍과 전자의 더 이상의 확산을 멈출 정도로 강할 때, 고갈 영역은 평형에 도달합니다.공핍 영역에 걸쳐 전장을 적분하면 내장 전압(접점 전압 또는 장벽 전압 또는 접촉 전위라고도 함)이 결정됩니다.

물리적으로는 (1) 전계에 의한 전하 캐리어 드리프트 및 (2) 공간적으로 변화하는 캐리어 농도에 의한 전하 캐리어 확산으로부터 반도체 디바이스에서의 전하 전달이 이루어진다.공핍영역의 P측에서는 전기전도율θ로 전계에 의해 홀이 표류하고 확산정수D에 의해 확산되는 순전류밀도를 다음과 같이 구한다.

${\bf {J}}=\sigma {\bf {E}}-eD\nabla p$ ${\bf {J}}=\sigma {\bf {E}}-eD\nabla p$ ${\bf {J}}=\sigma {\bf {E}}-eD\nabla p$ E - ${\bf {J}}=\sigma {\bf {E}}-eD\nabla p$ ${\bf {J}}=\sigma {\bf {E}}-eD\nabla p$ ${\bf {J}}=\sigma {\bf {E}}-eD\nabla p$ p \ $displaystyle$ \ $bf$ { J ${\bf {J}}=\sigma {\bf {E}}-eD\nabla p$ } ${\bf {J}}=\sigma {\bf {E}}-eD\nabla p$ = \ sigma \ $bf {$ E ${\bf {J}}=\sigma {\bf {E}}-eD\nabla p$ } - $eD$ \ $nabla$ p ${\bf {J}}=\sigma {\bf {E}}-eD\nabla p$ ,

${\bf {E}}$ 서 E $(\$ 는 ${\bf {E}}$ 전계, e는 기본 전하(1.6×10⁻¹⁹ 쿨롱), p는 구멍 밀도(단위 볼륨당 수)입니다.전장은 전계 방향을 따라 홀을 드리프트시키고 확산 홀은 농도가 감소하는 방향으로 이동하기 때문에 홀의 경우 양의 밀도 구배를 위한 음의 전류가 발생합니다.(캐리어가 전자일 경우 홀 밀도 p는 음의 부호를 가진 전자 밀도 n으로 대체됩니다; 경우에 따라서는 두 전자 모두및 홀을 포함해야 합니다.)두 개의 전류 성분이 균형을 이룰 때, 동적 평형의 p-n 결합 고갈 영역에서와 같이, 전류는 D와 θ에 관련된 아인슈타인 관계로 인해 0이 된다.

전방 바이어스

전방 바이어스(N 측에 대해 P 측에 양의 전압을 인가)는 고갈 영역을 좁히고 반송파 주입에 대한 장벽을 낮춥니다(오른쪽 그림에 표시).좀 더 자세히 설명하자면, 다수 통신사는 바이어스 장으로부터 에너지를 얻어 해당 지역으로 들어가 반대 전하를 중화시킬 수 있습니다.치우침이 심할수록 중화(또는 영역의 이온 스크리닝)가 더 많이 발생합니다.캐리어는 이온에 재결합할 수 있지만 페르미 에너지가 근접하기 때문에 열 에너지는 즉시 재결합 캐리어를 다시 전환시킵니다.바이어스가 강하여 고갈 영역이 매우 얇아지면 (접점 인터페이스를 통해) 전류의 확산 성분이 크게 증가하고 드리프트 성분이 감소합니다.이 경우 순전류는 P측에서N측으로 흐릅니다.반송파 밀도가 커서(적용된 바이어스 전압에 따라 기하급수적으로 변화), 접점이 전도성을 띠며 큰 전진 ^[3]전류를 허용합니다.전류에 대한 수학적 설명은 쇼클리 다이오드 방정식으로 제공됩니다.역바이어스 하에서는 낮은 전류가, 전진 바이어스 하에서는 큰 전류가 흐르는 것이 정류의 한 예입니다.

역편향

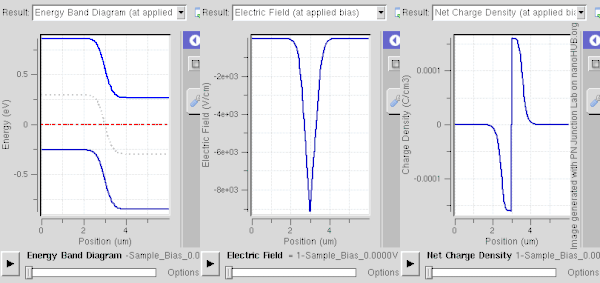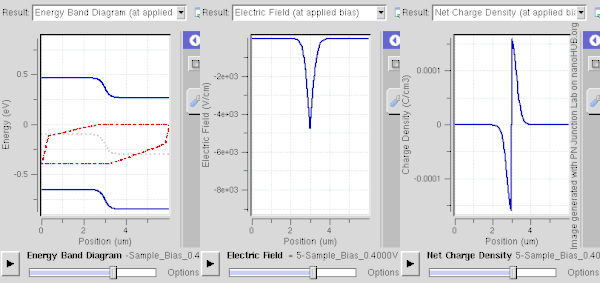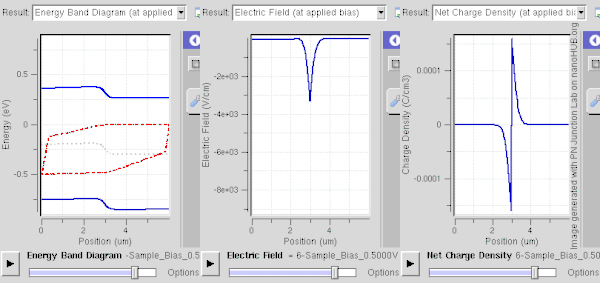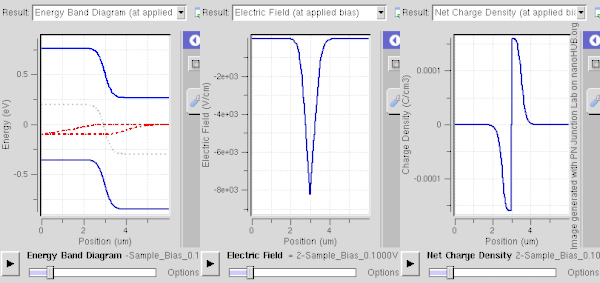
역바이어스(N 측에 대해 P 측에 음의 전압을 인가) 하에서는 공핍 영역에 걸친 전위 강하(전압)가 증가합니다.기본적으로, 대부분의 캐리어는 접합부에서 밀려나면서 더 많은 전하 이온을 남깁니다.따라서 공핍 영역은 넓어지고 그 장은 강해져 (접점 인터페이스를 통해) 전류의 드리프트 성분이 증가하고 확산 성분이 감소한다.이 경우 순전류는 N측에서P측으로 흐릅니다.반송파 밀도(대부분 마이너 캐리어)는 작고 역포화 전류가 매우 적게 흐릅니다.

고갈 레이어 폭 결정

그림 2와 같이 완전 고갈 분석에서, 전하가 한계점에서 갑자기 떨어져 근사하게 될 것이며, 실제로는 점차적으로 포아송 방정식으로 설명된다.플럭스^[4] 밀도의 양은 다음과 같습니다.

${\frac {Q_{n}}{x_{n}}&=qN_{d}\{\frac {Q_{p}}{x_{p}}}&=-qN_{a}\\end{aligned}}$

$Q_{n}$ 서 $({$ 과 $Q_n$ $({$ 는 $Q_{p}$ 각각 음전하와 양전하의 양, $({$ ${n$ $})$ 은 $x_n$ 음전하와 양전하의 거리이며 0을 $N_{a}$ 으로 N $({$ $N_$ ${$ a $x_{p}$ })은 음전하의 거리입니다.}와 $N_{a}$ $N_{d}$ { $displaystyle N_{$ d $N_{d}$ }는 $각각$ 수용체와 공여체 원자의 양이고 $q{displaystyle$ q $q$ }는 전자 전하입니다 $.$

$거리$ $d$ x {\ $displaystyle$ dx $}$ 에 $dx$ 대한 플럭스 $밀도$ D(\ $displaystyle$ D $)$ 의 $D$ 적분을 취하여 $전계$ E $(\displaystyle$ E $)($ 즉, 가우스의 법칙)를 결정하면 그림 2와 같이 두 번째 그래프가 생성됩니다.

$(\displaystyle E=sysfrac {int D,dx}{\epsilon _{s}}})$

여기서 $\epsilon _{s}$ s $\epsilon _{s}$ \ $displaystyle$ \ $abilon$ _ ${s}$ 는 $\epsilon _{s}$ 물질의 유전율입니다.거리에 대한 전계의 적분에 따라 $전위$ V(\ $displaystyle$ $\Delta V$ V $V$ 가 결정됩니다.이것은 그림 2와 같이 내장 $\Delta V$ $\Delta V$ V(\ $displaystyle\Delta$ V $)$ 와도 $\Delta V$ 같습니다.

$V=\int Edx=\Delta V$

마지막 방정식은 고갈층 $x_{n}$ $x_{n}$ n(\ $displaystyle x_{n})$ 의 $x_n$ 함수가 $전위$ V(\ $displaystyle$ V $V$ 에 의존하도록 배열됩니다.

${\frac {\aligned}x_{n}&=sq}{\frac {N_{a}}{N_{d}}{\frac {1}{N_{a}+N_{d}}(\x_{p}&=sqrt {\frac {2\flacilon _{s}}{q}}{\frac {N_{d}}{n_{a}}}}{\frac {1}{N_{a}+})N_{d}}(\Delta V)}}}\\end {aligned}$

요약하면 $($ 스타일 $x_{n})$ 과 $x_n$ $({$ style x_ ${p})$ 는 $x_{p}$ 중심에 대한 마이너스 및 플러스 고갈층 폭이며, $({$ N_ ${a$ })와 $N_{a}$ $({$ N_ ${d})$ 는 $N_{d}$ 각각 수용체와 도너 원자의 양이다. $({display style$ q})는 전자 전하이고 $\Delta V$ V $(\displaystyle\Delta$ V $)$ 는 $\Delta V$ 내장 전압이며, 일반적으로 독립 ^[4]변수입니다.

MOS 캐패시터에서의 형성

P형 실리콘의 금속 산화물 반도체 구조

고갈 영역의 또 다른 예는 MOS 캐패시터에서 발생합니다.P형 기판의 경우 오른쪽 그림에 나와 있습니다.처음에 반도체가 전하 중성이며, 홀에 의한 전하가 수용체 도핑 불순물에 의한 음전하와 정확히 균형을 이룬다고 가정한다.게이트에 정전하 Q를 도입함으로써 게이트에 정전압이 인가되면 게이트에서 가장 가까운 반도체에서 정전하 홀이 게이트 상의 정전하로 역류하고 저부 접점을 통해 장치를 빠져나간다.이동 구멍이 남아 있지 않기 때문에 절연되는 고갈된 영역을 남깁니다. 움직이지 않고 음으로 대전된 수용체 불순물만 남습니다.게이트에 정전하가 많을수록 게이트 전압이 인가되고 반도체 표면을 빠져나가는 구멍이 많아져 고갈 영역이 커집니다.(이 디바이스에서는 고갈폭에 제한이 있습니다.표면 근처의 얇은 층 또는 채널에서 캐리어의 반전층이 시작됨으로써 설정됩니다.위의 설명은 반전층이 형성되지 않을 정도로 낮은 양의 전압에 적용됩니다.)

게이트 재료가 벌크 반도체와 반대 타입의 폴리실리콘일 경우 위의 p-n 접합과 거의 동일한 방법으로 게이트가 기판과 전기적으로 단락되면 자발적 고갈 영역이 형성된다.자세한 내용은 폴리실리콘 고갈 효과를 참조하십시오.

공핍 영역의 총 폭은 적용된 역 바이어스와 불순물 농도의 함수입니다.

전하중립성의 원리는 양전하의 합이 음전하의 합과 같아야 한다고 말합니다.

n+N_{A}=p+N_{D},

여기서 n과 p는 자유 전자와 홀의 $N_{D}$ $({$ 와 $N_{D}$ $({$ 는 $N_{A}$ 각각 "길이 단위당" 이온화 공여체와 수용체의 수이다.이와 같이 $({$ 와 $N_{D}$ $({$ 는 $N_{A}$ 모두 도핑 공간 밀도로 볼 수 있습니다.완전 이온화와 n $n,p\ll N_{D},N_{A}$ $n,p\ll N_{D},N_{A}$ $n,p\ll N_{D},N_{A}$ $n,p\ll N_{D},N_{A}$ $n,p\ll N_{D},N_{A}$ $n,p\ll N_{D},N_{A}$ $(\$ n, $p\l N_{D}, N_{A$ 를 가정하면 다음과 같습니다.

qN_{A}w_{P}\approx qN_{D}w_{N}\,

qN_{A}w_{P}\approx qN_{D}w_{N}\,

qN_{A}w_{P}\approx qN_{D}w_{N}\,

qN_{A}w_{P}\approx qN_{D}w_{N}\,

qN_{A}w_{P}\approx qN_{D}w_{N}\,

N W

qN_{A}w_{P}\approx qN_{D}w_{N}\,

\

displaystyle qN_{A}w_{P}\about qN_{D}w_{N

$w_{P}$ 서 w P $(\$ 와 $w_{P}$ w $(\$ 은 $w_{N}$ 각각 p 및 n 반도체의 고갈 폭입니다.이 조건을 통해 순 음의 수용체 전하가 순 양의 기증자 전하의 균형을 정확히 유지합니다.이 경우 총 $w=w_{N}+w_{P}$ 폭은 w $w=w_{N}+w_{P}$ $w=w_{N}+w_{P}$ N + $w=w_{N}+w_{P}$ P { $displaystyle$ w = $w$ _ { $N}+w_{P$ 고갈 폭의 완전한 파생이 ^[5]참조에 제시되어 있습니다.이 유도는 포아송 방정식을 1차원, 즉 야금 접합부에 수직인 차원으로 푸는 것에 기초한다.전기장은 공핍폭(위 그림 참조)을 벗어나 0이므로 가우스의 법칙은 각 영역의 전하 밀도가 균형을 이룬다는 것을 의미합니다. 이 하위 섹션의 첫 번째 방정식에서 알 수 있습니다.각 영역을 분리하여 처리하여 각 영역의 전하 밀도를 포아송 방정식으로 치환하면 결국 고갈폭의 결과로 이어진다.고갈 폭의 결과는 다음과 같습니다.

\displaystyle w\apprough \left [{\frac {2\epsilon _{r}\epsilon _{0}}{q}}\left ({\frac {N_{A}+N_{D}}}\right)\left (V_{bi}-V\fright)

여기서 $\epsilon _{r}$ r $\epsilon _{r}$ {\ $displaystyle \epsilon$ _ ${r}$ 은 $\epsilon_r$ 반도체의 상대 유전 유전율, $V_{bi}$ $V_{bi}$ { $displaystyle V_{$ bi}는 $V_{bi}$ 내장 전압 $,$ V {\ $displaystyle$ V $}$ 는 $V$ 인가 바이어스입니다.고갈 영역은 n개 영역과 p개 영역 사이에 대칭적으로 분할되지 않습니다. 이는 가볍게 도핑된 ^[6]쪽으로 향합니다.좀 더 완전한 분석은 고갈 영역의 ^[7]가장자리 근처에 아직 일부 캐리어가 있다는 것을 고려할 것이다.그러면 위의 마지막 괄호 세트에 -2kT/q 항이 추가됩니다.

MOS 콘덴서의 고갈 폭

p-n 접합에서와 같이, 여기서의 지배 원칙은 전하 중립성이다.P형 기판을 가정해 봅시다.영역 A와 함께 게이트에 양의 전하 Q를 배치하면 게이트 전하의 정확한 균형을 맞추기 위해 충분한 양의 음의 수용체가 노출되는 깊이까지 구멍이 고갈됩니다.도판트 밀도가 $N_{A}$ 부피당 $(\$ 리셉터라고 $N_{A}$ 가정하면 전하 중성성은 관계를 만족시키기 위해 고갈 폭 w가 필요합니다.

{{displaystyle Q/A=qN_{A}w,}

공핍폭이 충분히 넓어지면 전자는 반도체 산화물 계면에서 매우 얇은 층으로 나타나는데, 이는 P형 물질에 널리 퍼져 있는 구멍에 반대 방향으로 대전되기 때문에 반전층이라고 불립니다.반전층이 형성되면 게이트 차지Q의 증가에 따라 고갈폭의 확대가 정지됩니다.이 경우, 더 많은 전자를 반전층 안으로 끌어당김으로써 중립성이 달성된다.MOSFET에서는 이 반전층을 채널이라고 부릅니다.

공핍층 및 밴드 벤딩 전계

고갈층과 관련된 효과는 밴드 벤딩으로 알려져 있습니다.이 효과는 고갈층의 전계가 게이트의 (최대) $E_{m}$ $E_{m}$ {\ $displaystyle E_{m}$ 에서 $E_{m}$ 고갈 ^[8]폭의 가장자리의 0으로 선형적으로 변화하기 때문에 발생합니다.

E_{m}={Q\over A\epsilon_{0}=qN_{A}{w\over \epsilon_{0}},

여기서 $\epsilon _{0}$ 0 \ $displaystyle$ \ $silon$ _ { $0$ } = $\epsilon _{0}$ 8.854×10⁻¹² F/m, F는 파라드, m은 미터이다.이 선형으로 변화하는 전장은 공간 내에서 2차적으로 변화하는 전위를 유도합니다.에너지 수준 또는 에너지 대역은 이 전위에 따라 구부러집니다.

「」를 참조해 주세요.

레퍼런스

^ Robert H. Bishop (2002). The Mechatronics Handbook. CRC Press. ISBN 0-8493-0066-5.
^ John E. Ayers (2003). Digital Integrated Circuits: Analysis and Design. CRC Press. ISBN 0-8493-1951-X.
^ Sung-Mo Kang and Yusuf Leblebici (2002). CMOS Digital Integrated Circuits Analysis & Design. McGraw–Hill Professional. ISBN 0-07-246053-9.
^ ^a ^b "Electrostatic analysis of a p-n diode". ecee.colorado.edu. Retrieved 2018-09-26.
^ Pierret, Robert F. (1996). Semiconductor Device Fundamentals. pp. 209 to 216.
^ Sasikala, B; Afzal Khan; S. Pooranchandra; B. Sasikala (2005). Introduction to Electrical , Electronics and Communication Engineering. Firewall Media. ISBN 978-81-7008-639-0.
^ Kittel, C; Kroemer, H. (1980). Thermal Physics. W. H. Freeman. ISBN 0-7167-1088-9.
^ Wayne M. Saslow (2002). Electricity, Magnetism, and Light. Elsevier. ISBN 0-12-619455-6.

[1] Robert H. Bishop (2002). The Mechatronics Handbook. CRC Press. ISBN 0-8493-0066-5.

[2] John E. Ayers (2003). Digital Integrated Circuits: Analysis and Design. CRC Press. ISBN 0-8493-1951-X.

[3] Sung-Mo Kang and Yusuf Leblebici (2002). CMOS Digital Integrated Circuits Analysis & Design. McGraw–Hill Professional. ISBN 0-07-246053-9.

[:0-4] "Electrostatic analysis of a p-n diode". ecee.colorado.edu. Retrieved 2018-09-26.

[5] Pierret, Robert F. (1996). Semiconductor Device Fundamentals. pp. 209 to 216.

[6] Sasikala, B; Afzal Khan; S. Pooranchandra; B. Sasikala (2005). Introduction to Electrical , Electronics and Communication Engineering. Firewall Media. ISBN 978-81-7008-639-0.

[7] Kittel, C; Kroemer, H. (1980). Thermal Physics. W. H. Freeman. ISBN 0-7167-1088-9.

[8] Wayne M. Saslow (2002). Electricity, Magnetism, and Light. Elsevier. ISBN 0-12-619455-6.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Search

고갈 지역

네임스페이스

더

목차