황소 그래프

황소 그래프
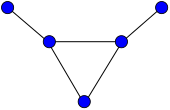황소 그래프
정점	5
가장자리	5
반지름	2
지름	3
둘레	3
자동형성	2(Z/2Z)
색수	3
색도 지수	3
특성.	플라나르 단위 거리
그래프 및 모수 표

그래프 이론의 수학적 분야에서 bull 그래프는 두 개의 분리형 펜던트 가장자리가 있는 삼각형의 형태로 5개의 정점과 5개의 가장자리를 가진 평면형 비방향 그래프다.^[1]

색도 번호 3, 색도 지수 3, 반지름 2, 직경 3, 둘레 3을 가지고 있다.또한 자기 완성 그래프, 블록 그래프, 분할 그래프, 구간 그래프, 발톱 없는 그래프, 1Vertex 연결 그래프, 1Edge 연결 그래프 등이 있다.

황소가 없는 그래프

그래프는 유도 서브그래프로 황소가 없는 경우 황소가 없다.삼각형이 없는 그래프는 황소가 없는 그래프인데, 모든 황소가 삼각형을 포함하기 때문이다.강인한 완벽한 그래프 정리는 일반 그래프에 대한 증명보다 훨씬 이전에 황소 프리 그래프에 대해 입증되었으며,^[2] 황소 프리 퍼펙트 그래프의 다항식 시간 인식 알고리즘이 알려져 있다.^[3]

마리아 추드노브스키와 슈무엘 사프라는 황소가 없는 그래프를 더 일반적으로 연구해 왔으며, 그러한 그래프는 반드시 큰 패거리나 큰 독립된 집합(황소 그래프를 위한 Erd–s-Hajnal 추측)^[4]을 가지고 있어야 한다는 것을 보여주고, 이러한 그래프에 대한 일반적인 구조 이론을 발전시켰다.^[5][6][7]

색채 및 특성 다항식

색도 다항식이${\displaystyle }$( ${\displaystyle \mathrm{x}}$- 2${\displaystyle }$)${\displaystyle }$( ${\displaystyle x}$- ${\displaystyle 1{}^{}}$) 3 ${\displaystyle {}^{}}$ ${\displaystyle (x-2)(x-1)^{3}x}$과 같은 세 개의 그래프$.$

bull 그래프의 색도 다항식은${\displaystyle }$( ${\displaystyle \mathrm{x}}$- 2${\displaystyle }$)${\displaystyle }$( x${\displaystyle }$- ${\displaystyle 1{}^{}}$) ${\displaystyle {3\mathrm{}}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle (x-2)(x-1)^{3}x}$ 입니다$.$다른 두 개의 그래프는 황소 그래프와 색상으로 동일하다.

그것의 특징적인 다항식은 -${\displaystyle x}$( ${\displaystyle {x\mathrm{}}^{}}$ 2${\displaystyle {}^{}}$- ${\displaystyle \mathrm{x}}$- 3${\displaystyle }$)$$( x ${\displaystyle {2\mathrm{}}^{}}$+ ${\displaystyle 1}$ )$displaystyle -x(x^{2}-x-3$) $(x^{2}+x-1)}$ 입니다$.$

그것의 Tutte 다항식은 ${\displaystyle {x\mathrm{}}^{}}$ 4${\displaystyle {}^{}}$+ ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$+ ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle$ x$^{4}+x^{3}+x^{2}y}$ 입니다$.$

참조