제로 억제 의사결정도

이 문서에는 참고 자료, 관련 읽기 또는 외부 링크가 포함되어 있지만 인라인 인용이 부족하여 출처가 불분명합니다. 좀 더 정밀한 인용문을 도입하여 이 글의 개선에 도움을 주시기 바랍니다.(2018년 11월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

제로 억제 결정 다이어그램(ZSDD 또는 ZDD)은 가변 순서가 고정된 특정 종류의 이진 결정 다이어그램(BDD)입니다.이 데이터 구조는 특히 특정 조합 문제에 적합한 집합의 규범적인 콤팩트한 표현을 제공합니다.OBDD(Ordered Binary Decision Diagruction Diagram) 축소 전략을 기억하십시오. 즉, 두 출력 에지가 동일한 노드를 가리킬 경우 노드가 하위 노드 중 하나로 교체됩니다.반대로 ZDD 내의 노드는 그 양의 엣지가 단말 노드 0을 가리키면 그 음의 자노드로 치환된다.이를 통해 스파스 집합의 압축이 개선된 대체적인 강력한 정규 형식을 제공합니다.미나토 신이치가 1993년에 고안한 삭감 룰에 근거하고 있다.

배경

Binary Decision Diagram에서 Boolean 함수는 루트, 방향, 비순환 그래프로 나타낼 수 있습니다.이 그래프는 여러 개의 의사결정 노드와 터미널 노드로 구성됩니다.1993년 일본의 미나토 신이치는 조합 문제를 해결하기 위해 랜달 브라이언트의 BDD를 수정했다.그의 "Zero-Suppressed" BDD는 희박한 비트 벡터의 집합을 표현하고 조작하는 것을 목표로 합니다.문제의 데이터가 길이 n의 비트 벡터로 표현될 경우 변수 할당에 대응하는 벡터가 세트 내에 있을 때 벡터의 서브셋은 n개의 변수에 걸쳐 부울 함수로 표현될 수 있다.

Bryant에 따르면, 논리 함수의 형태를 사용하여 곱의 합과 관련된 문제를 표현하는 것이 가능하다고 합니다.이러한 형식은 종종 기호 0, 1 및 -를 포함하는 문자열로 나타나는 "cubes" 집합으로 나타납니다. 예를 들어 함수${\displaystyle }$(${\displaystyle {\stackrel{}{}1}_{\mathrm{}}}$ 1${\displaystyle {}_{}{x\mathrm{}}_{}}$ x${\displaystyle {}_{}}$2) ${\displaystyle (}$ ( ${\displaystyle {\stackrel{}{}2}_{\mathrm{}}}$ 2$$ ${\displaystyle {x\mathrm{}}_{}}$ 3) { $displaystyle$( \$bar$ {$x } _$ { { {1} \ land $x_{2$} \$lor$ ( \ bar {$x$} _ { x } _ { \ } { } { } \ $3 plus$ 3 $})$에서 벡터의 수 2n보다 적다 \{01-,-11,-00\}}. 10,01,, OO각각 기호 1,0이고 그리고 –을 나타내기 위해 비트를 사용하여Playstyle,}. 비트 벡터의 집합는 것은 희박하다는톤 비트 벡터와{011000,001010,000101}{\displaystyle\와 같이{011000,001010,000101\}의 형태에 위의 집합 통보서를 나타낼 수 있he 비트 벡터의 최대 수, 세트에는 0과 같은 요소가 다수 포함되어 있습니다.이 경우 노드 변수를 1로 설정하면 함수가 0을 출력할 경우 노드를 생략할 수 있습니다.이는 특정 비트 위치에서 1이 벡터가 세트 내에 없음을 암시하는 조건에서 볼 수 있습니다.스파스 세트의 경우 이 상태는 일반적이기 때문에 많은 노드를 제거할 수 있습니다.

Minato는 ZDD가 특히 2단계 로직 최소화의 고전적인 문제, 나이트 투어 문제, 고장 시뮬레이션, 타이밍 분석, N-queen 문제 및 약한 분할과 같은 조합 문제에 적합하다는 것을 증명했습니다.ZDD를 사용함으로써 OBDD에서의 n비트 벡터 세트의 표현 크기를 n배까지 줄일 수 있다.실제로 최적화는 통계적으로 유의합니다.

정의들

Zero-Suppressed Decision Diagram(ZDD; 제로 억제 의사결정 다이어그램)을 다음과 같이 임의의 방향 비순환 그래프로 정의합니다.

1. 터미널 노드는 다음 중 하나입니다.

• 유닛 패밀리 $\{{\displaystyle }$ $}$ { $displaystyle$\ { \ $emptyset \$ } $$（ set set),),),),세트)를 나타내는 특수 노드 또는
• 빈 패밀리 "\$displaystyle \emptyset$을 나타내는 특수 노드$.$

2. 각 비터미널 노드는 다음 조건을 충족합니다.

a. 노드에는 양의 정수 v로 라벨이 붙어 있습니다.이 라벨은 일의일 필요는 없습니다.

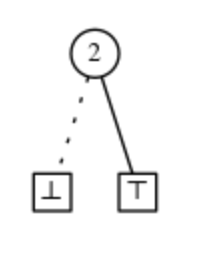
b. 노드의 등급은 2입니다.나가는 에지 중 하나는 "LO"이고 다른 하나는 "HI"입니다. (그림에서 LO 에지의 경우 점선을 그리고 HI 에지의 경우 실선을 그릴 수 있습니다.)

c. 수신처 노드는 터미널 또는 v보다 엄밀하게 큰 정수로 라벨이 부착되어 있습니다.따라서 모서리 방향은 레이블에서 유추할 수 있으므로 다이어그램에서 화살촉을 생략할 수 있습니다.

d. HI 에지는 points노드를 가리키지 않습니다.

3. 도수가 0인 노드가 정확히 1개 있습니다.루트 노드는 terminal 또는 다이어그램에서 가장 작은 정수로 라벨이 지정됩니다.

4. 두 노드의 라벨이 동일한 경우 LO 또는 HI 가장자리가 다른 노드를 가리킵니다.즉, 용장 노드는 존재하지 않습니다.

HI 엣지가 node노드를 가리키거나 조건4를 유지할 수 없는 경우에는 Z를 비감소 ZDD라고 부릅니다.컴퓨터 프로그램에서는 부울 함수를 비트로 표현할 수 있으므로 the노드와 node노드는 1과 0으로 나타낼 수 있다.위의 정의에서 BDD에 2개의 규칙을 적용함으로써 조합 세트를 효율적으로 나타낼 수 있습니다.

1. 엣지가 0 터미널 노드를 가리키는 노드를 모두 제거합니다(그림 1 ).그런 다음 모서리를 다른 하위 그래프에 직접 연결합니다.

2. 모든 동등한 서브그래프를 원래의 BDD와 동일하게 공유합니다.

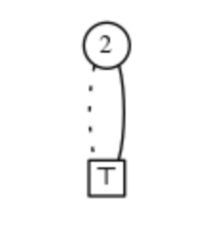
입력 변수의 수와 순서가 고정되면 제로 억제 BDD는 부울 함수를 고유하게 나타냅니다(그림 2에서 증명된 바와 같이 BDD를 사용하여 부울 바이너리 트리를 나타낼 수 있습니다).

집합 패밀리 표시

F를 ZDD로 합니다.v를 루트 노드로 합니다.그 후, 다음과 같이 입력합니다.

1. v = ,이면 다른 노드가 있을 수 없으며 F는 빈 패밀리인 the를 나타냅니다.

2. v = ,이면 다른 노드가 있을 수 없으며, F는 빈 집합 { }. }만 포함하는 패밀리를 나타냅니다.이것은 유닛 패밀리라고 불리며 로 나타냅니다.

3. v에 두 자녀가 있는 경우v0을 LO 노드로 하고 v1을 HI 노드로 합니다.Fi를 vi에 뿌리를 둔 ZDD로 나타내는 패밀리로 하자. 이것은 유도 증명으로 나타낼 수 있다.그럼 F는 가족을 나타냅니다.

$\displaystyle F_{0}\cup \{\alpha \cup \{v\}\mid \alpha \in F_{1}\}$

LO 분기는 F에서 v를 포함하지 않는 집합으로 나타낼 수 있습니다: $F{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle =}$ {${\displaystyle \alpha }$ : α${\displaystyle \delta }$F , ${\displaystyle v}$ α$$} {$display F_{0$} = \{\alpha $:\alpha$ \$in$F , v$\notin \}$

그리고 F의 집합으로서의 HI 분기는 v: ${\displaystyle F}$ ${\displaystyle {1\mathrm{}}_{}}$ $=$ {${\displaystyle \alpha }$ ${\displaystyle \{}$ { ${\displaystyle v}$ ${\displaystyle \}}$ : α${\displaystyle f}$F , ${\displaystyle v\alpha }$ α$$ { $displaystyle F_{1}=\{\alpha$ \$backslash$\{$v\}} :\alpha$ \$in F,v\$alpha \}를 포함한다.

예

그림 3: 패밀리 $\varnothing {\displaystyle \mathrm{}}$∅ { ${\displaystyle \mathrm{\varnothing \varnothing }}$ ${\displaystyle \{}$ { ${\displaystyle 2}$ ${\displaystyle \}=}${ 2 ${\displaystyle \}}$ ${\displaystyle \}}$ { { ${\displaystyle 2}$ } $}$ { { $displaystyle$\$emptyset \ cup$\ { 2 \ } = \ { \ { 2 \ $}$} = \ { 2 \ $displaystyle$ e$_$ {$2$} } $ary{\displaystyle {}_{}}$ an an anary 。Elementary 패밀리는${\displaystyle }${$n}$ {displaystyle $\{\n$ 형식으로 구성되며 ${\displaystyle {en}_{}}$ ${$ 로 $표시$됩니다.

${\displaystyle \mathrm{그림}}$ 4: 패밀리${\displaystyle }${${\displaystyle \mathrm{}\varnothing }$ ${\displaystyle \}}$ ∅ { ${\displaystyle \varnothing \}=}$ { ${\displaystyle ,}$ ${\displaystyle 、}$ { ${\displaystyle 2}$} $}$ { { $displaystyle$\ { \ \ $emptyset$ \ { \ { \ \$cup$ \ { 2 \ } \ } = \ { \ { \ { $2$\ $emptyset , \$ } } = \ { \ { \ { \ } } } }

그림 5: {${\displaystyle 2}$ ${\displaystyle \}}$ 패밀리 $\{{\displaystyle }$}${\displaystyle \cup }$ { ${\displaystyle \mathrm{\varnothing }1}$ ${\displaystyle \}=}${ { ${\displaystyle 1}$ ${\displaystyle \}}$, { ${\displaystyle 2}$ ${\displaystyle \}}$} $}$ { $displaystyle$\ { \ { \ { \ { \ { 2 \ } \ $cup$ \ { \ { \ \ $emptyset$\ $cup$\ { 1 \ } = \ { \ { \ { \ $1$\ , \ $}$ } } } } = \ { \ { \ { \ { \ { \ { 1 } } } } }

${\displaystyle \mathrm{그림}}$ 6: {${\displaystyle }$1 ${\displaystyle \}}{\displaystyle \{}$ { ${\displaystyle 2}$ ${\displaystyle \}=}${ { ${\displaystyle 1}$,${\displaystyle }$2 ${\displaystyle \}}$ $}$ { { $displaystyle$\ { \ { \ { \ { 1 \ } \ $cup$\ { 2 \ } = \ { \ { \ { 1, 2 \$$} \ } } = \ { \ { \ { 1 , $2$ \ } } } }

특징들

ZDD의 한 가지 특징은 조합 세트가 같은 한 형식이 입력 변수의 수에 의존하지 않는다는 것입니다.그래프를 생성하기 전에 입력 변수 수를 수정할 필요가 없습니다.ZDD는 조합으로 표시되지 않는 객체의 변수를 자동으로 억제하므로 스파스 조합을 효율적으로 조작할 수 있습니다.ZDD의 또 다른 장점은 그래프 내의 1-경로 수가 조합 세트의 요소 수와 정확히 같다는 것입니다.원래의 BDD 에서는, 노드 삭제에 의해서 이 속성이 파손됩니다.따라서 ZDD는 단순한 BDD보다 조합 세트를 나타내는 것이 좋습니다.단, 그림 7과 같이 일반적인 부울 함수를 나타낼 때는 원래의 BDD를 사용하는 것이 좋습니다.

기본 조작

여기에서는, 원래의 BDD와 조금 다르기 때문에, ZDD의 기본적인 조작을 나타냅니다.아래 표에서 생성된 예에 대해서는 그림 8을 참조해 주십시오.

Empty()는 ö(빈 집합)를 반환합니다.

Base()는 {0}을(를) 반환합니다.

Subset1(P, var)은 var = 1과 같은 P의 서브셋을 반환합니다.

Subset0(P, var)은 var = 0과 같은 P의 하위 집합을 반환합니다.

Change(P, var)는 var가 반전될 때 P를 반환합니다.

Union(P, Q)이 $$한다( P${\displaystyle q}$Q { $displaystyle$ P$\cup$ Q$\}$ )

Intsec(P, Q)이 $$한다( P${\displaystyle q}$Q { $displaystyle$ P\$cap$ Q$\}$ )

Diff(P, Q)가 $$됩니다( P${\displaystyle }$-$$ { $display style$ P -$$Q$$} )

Count(P)는 P$${\$display\left\vert$ P$\right\vert$를 ${\displaystyle 반환}$합니다.(요소의 수)

ZDD 에서는, 원래의 BDD 에서는 불가결한 조작인 NOT 조작은 없습니다.그$$ 이유는 유니버설 $집합{\displaystyle }$U를 정의하지 않으면 보집합 P$$${\$ ${\$$displaystyle$ {$P$$\}\}$를 계산할 수 없기 때문입니다.ZDD에서는 ${\$ ${\displaystyle$ {$P}}$는 Diff(U, P)로$$ 계산할 수 있습니다.

알고리즘

${\displaystyle P}$ $=$ ${\displaystyle {P\mathrm{}}_{}}$ 0${\displaystyle {}_{}}$+ ${\displaystyle {P\mathrm{}}_{}}$ 1 $displaystyle$\left $\vert$ P$\right \vert$ =\$left \vert P_{0}\right \vert +\left \vert$ P_{$1}\right \vert$})$$이라고 가정하면 ZDD의 세트 수를 재귀적으로 계산하여 54 멤버를 설정할 수 있습니다.랜덤 액세스가 고속이며, 일련의 세트에 대해 가능한 모든 조작을 ZDD 상에서 효율적으로 실행할 수 있습니다.

미나토에 따르면 ZDD에 대한 상기 조작은 원래의 BDD와 마찬가지로 재귀적으로 실행할 수 있다.알고리즘을 간단히 설명하기 위해 절차를 정의한다.Getnode(top, P0, P1)변수 톱의 노드를 반환하고 2개의 서브그래프 P0과 P1을 반환한다.uniq-table이라고 불리는 해시 테이블을 사용하여 각 노드를 고유하게 유지할 수 있습니다.노드 제거 및 공유는 다음 사용자만이 관리할 수 있습니다.Getnode().

Getnode(위, P0, P1) { if (P1 == ö)가 P0을 반환하고 /* 노드 제거 */P = uniq-table에 (위, P0, P1)가 있는 노드를 검색합니다. (P가 존재하는 경우) P; /* 노드 공유 */P = P가 있는 노드 생성(위, P1; 01)

사용.Getnode()그 후, 다음과 같이 그 외의 기본적인 조작을 나타낼 수 있습니다.

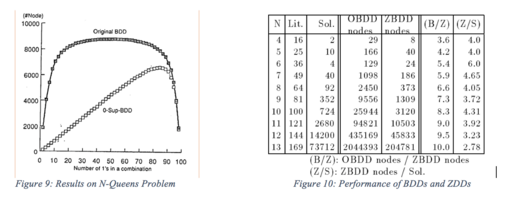
Subset1 (P, var) { if (P.top < var) ret ö; (P.top == var) return P1; (P.top > var) getnode (P.top, Subset1(P0, var), Subset1(P1, var)};

Subset0 (P, var) { if (P.top < var) ret ö; (P.top == var) return P0; (P.top > var) getnode (P.top, Subset0(P0, var), Subset0(P1, var)};

만약 반환 Q(P== ø)변화{;만약(P== Q)반환 P;연합(P, Q)만약(Q== ø)반환 P만약(P.top>Q.top)반환 Getnode(P.top,{만약(P.top>var)반환 Getnode(P.top 변경(Po는 교정된 동력,'), Change(P1,')한 경우-(P.top<>var)반환 Getnode(초본, ø, P);만약(P.top ==의 ')반환 Getnode,(초본, P1, Po는 교정된 동력).}(P,').연합(P0, Q), P1), (P.top < Q.top)가 Getnode(Q.top, Union(P, Q0), Q1), (P.top == Q.top)가 Getnode(P.top, Union(P0, Q0), Union(P1, Q1)을 반환하는 경우;

Intsec (P, Q) { if (P == ö) return > if (P == ö) return > if (P == Q) return P, if (P.top > Q.top) return Intsec (P.top) return > Q.

Diff (P, Q) { if (P == ö) return ö; if (Q == ö) return P; if (P == Q) return ö; if (P.top > Q.top) return Getnode (P.top, Diff (P0, Q.top) returning P. if (Q) returning)

카운트(P) {if (P == ö)가 0을 반환하고, (P == {ö})이(가) 1을 반환하고, 반환 카운트(P0) + 카운트(P1);}

이러한 알고리즘은 최악의 경우 변수 수에 대해 기하급수적으로 시간이 걸리지만 BDD에서도 마찬가지로 최근 작업 결과를 기억하는 캐시를 사용함으로써 성능을 향상시킬 수 있습니다.캐시는 동등한 하위 그래프에 대한 중복 실행을 방지합니다.그림 9와 그림 10과 같이 중복되지 않는 한 알고리즘은 그래프 크기에 비례하는 시간에 작동할 수 있습니다.

어플

사전으로서의 ZDD

ZDD는 예를 들어 Stanford GraphBase에서 WORDs(5757)를 설정하는 등 영어의 5글자를 나타내는 데 사용할 수 있습니다.이를 위한 한 가지 방법은${\displaystyle }$5개의 숫자$($ 1, ${\displaystyle ...,}$ ${\displaystyle {x\mathrm{}}_{}}$ $5$2$(x_{$1}, $...$${\displaystyle {\mathrm{x\_}}_{}{}_{}}$$25$$})$의 경우에만 1로 $정의$되는${\displaystyle }함수{\displaystyle }$(${\displaystyle {x\mathrm{}}_{}}$${\displaystyle {}_{}}$1, ${\displaystyle ...,}$${\displaystyle {}_{}}$x_${$$25$})를 고려하는 것입니다${\displaystyle .}$$..,{\displaystyle }$ ( ${\displaystyle {}_{}}$ ${\displaystyle {21}_{}{}_{}}$. , x ${\displaystyle {25}_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}${ $displaystyle$ ( x$_$ { $21$, x$_$ { $25$$}$ _ { } )_$$$\{$$2}}$${\displaystyle }$2 ( ${\displaystyle 00001{}_{}}$ ($00001{\displaystyle }$$)$$2$ (... , z $= 11010$ (${\displaystyle \mathrm{예}}$:${\displaystyle 0}$, )${\displaystyle 1,}$ ${\displaystyle 0,1}$, ${\displaystyle 1}$,${\displaystyle 0,}$ ${\displaystyle 0,}$ ${\displaystyle {\mathrm{x}}_{}}$ 25${\displaystyle {}_{}}$ $= x$ $({displaystyle f(0,0,$1,1$,0,1$,$1$,1,1,1,1$,0,$1,$0,1$,$1,0,$0,1,1,1,$0,0$,0$,0,x_{25$25개 변수의 함수는 Z(f) = 6233개의 노드를 가지며, 이는 5757개의 단어를 표현하기에 나쁘지 않습니다.이진 트리, 시도 또는 해시 테이블에 비해 ZDD는 단순 검색을 완료하는 데 최적이지는 않을 수 있지만 부분적으로만 지정된 데이터 또는 대략적인 키와 일치해야 하는 데이터를 검색하는 데 효율적입니다.복잡한 쿼리를 쉽게 처리할 수 있습니다.게다가 ZDD는 많은 변수를 수반하지 않습니다.실제로 ZDD를 사용하면 이들 5개의 문자 단어를 스파스 $함수{\displaystyle }$F$($.${\displaystyle }$.${\displaystyle }$. , ${\displaystyle {z\mathrm{}}_{}{}_{}{}_{}}$ , 2${\displaystyle }$,${\displaystyle }$. , ${\displaystyle {}_{}{}_{}{2\mathrm{}}_{}}$,${\displaystyle }$.${\displaystyle }$, . , . , .${\displaystyle }$, $z$ $)(표시 스타일$ F($a_{1$} , $z_{2}$ , $z_{5})$로서 나타낼 수 있습니다.example은 두 번째 문자가 "a"인지 여부를 결정합니다."crazy"라는 단어를 나타내려면 ${\displaystyle {c\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {r2\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {3\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {z\mathrm{}}_{}}$ 4 $=$ ${\displaystyle {}_{}}$ ${\displaystyle {5\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle 1}${ $displaystyle c_{1$} =$a_{$2$} = a_{$3}=$z_{4$}=$y_${5$}=$1}이고 $다른{\displaystyle {}_{}}$ 모든 변수가 0일 때 F를 참으로 만들 수 있습니다.따라서 F는 5757개의 서브셋$\{{\displaystyle }$ ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}{}_{}}$2, ${\displaystyle {i\mathrm{}}_{}{}_{}}$, ${\displaystyle {c\mathrm{}}_{}{}_{}}$, h $}{$ $displaystyle$\ {$w_{1}, h_{2}, i_{$3}, $c_{4}, h_{5$ 등으로 구성된 패밀리로 간주할 수 있습니다.이 130개의 변수를 사용하는 경우 ZDD 크기 Z(F)는 실제로는 6233이 아닌 5020입니다.Knuth에 따르면, BDD를 사용하는 B(F)의 등가 크기는 46,189로 Z(F)보다 상당히 크다.비슷한 이론과 알고리즘을 가지고 있음에도 불구하고 ZDD는 이 문제에 대한 BDD보다 상당히 큰 마진을 가지고 있습니다.따라서 ZDD를 사용하면 BDD에 너무 부담이 큰 특정 쿼리를 수행할 수 있습니다.초급 패밀리에서 복잡한 서브셋 패밀리를 쉽게 구성할 수 있습니다.특정 패턴을 포함하는 단어를 검색하려면 ZDD에서 패밀리 대수를 사용하여 (${\displaystyle F}$/${\displaystyle P}$ )${\displaystyle p}$P \ $displaystyle ( F$ /$P$ ) \ $sqcup$ P$$$$（ P p p p ） p 1${\displaystyle {}_{}{h3\mathrm{}}_{}}$ ${\displaystyle {5\mathrm{}}_{}}$ \ $displaystyle a$_ { 1$$} \ $sqcup h _ 5$） 。

단순한 경로를 나타내는 ZDD

ZDD를 사용하여 단순한 경로를 무방향 그래프로 나타낼 수 있습니다.예를 들어, 3×3 그리드의 왼쪽 상단 모서리(그림 11 참조)에서 오른쪽 하단 모서리까지 두 번 방문하지 않고 12가지 방법이 있습니다.

이러한 경로는 그림 13에 나타낸ZDD로 나타낼 수 있습니다.여기서 각 노드 mn은 "경로에 m과 n 사이의 호가 포함되어 있습니까?"라는 질문을 나타냅니다.예를 들어 13과 12 사이의 LO 브랜치는 경로에 1에서2까지의 호가 포함되어 있지 않은 경우 다음으로 문의해야 할 것은 1에서2까지의 호가 포함되어 있는지 여부입니다.노드 12에서 나가는 LO 브런치가 없는 것은 1에서3으로 가지 않는 패스는 1에서2로 가야 함을 나타냅니다.이 ZDD에서는 ZDD의 노드 13, 36, 68, 89에서 HI 브랜치를 취함으로써 제1 패스를 얻는다(단순히 go로 가는 LO 브랜치는 생략된다).그림 13의 ZDD는 어떠한 방법으로도 의미가 없어 보일 수 있지만, 그리드가 커짐에 따라 ZDD의 장점이 분명해집니다.예를 들어 8x8 그리드의 경우 코너에서 코너로 이동하는 단순 경로의 수는 789,360,053,252(Knuth)입니다.경로는 33580 노드에서 ZDD를 사용하여 나타낼 수 있습니다.

간단한 경로의 실제 예는 Randal Bryant에 의해 제안되었습니다. "만약 내가 미국 대륙을 드라이브 투어하고, 모든 주(州)를 방문하고, 각 주를 한 번만 통과하고 싶다고 가정한다면.총 거리를 최소화하려면 어떤 경로를 선택해야 합니까?그림 14는 이 로드맵에 대한 무방향 그래프를 보여 주며, 숫자는 인접한 수도들 사이의 최단 거리를 나타낸다.문제는 가장 작은 전체 길이의 해밀턴 경로를 형성하는 이러한 에지 중 서브셋을 선택하는 것입니다.이 그래프의 모든 해밀턴 경로는 메인주(ME)의 Augusta에서 시작하거나 끝나야 합니다. CA에서 시작한다고 가정합니다.CA에서 ME로의 모든 경로를 특징짓는 ZDD를 찾을 수 있는데, Knuth에 따르면 이 ZDD는 7850개의 노드만을 가지고 있으며, CA에서 ME로의 단순한 경로가 정확히 437,525,772,584개 가능하다는 것을 효과적으로 보여주고 있다.에지 수에 따라 생성 함수는 다음과 같습니다.

$displaystyle 4z^{11}$$$$+33385461z^{46}+1407075z^{47$

따라서 이러한 가장 긴 경로는 2,707,075의 크기를 가진 해밀턴 경로입니다. 이 경우 ZDD는 단순 경로와 해밀턴 경로에 효율적입니다.

8개의 큐 문제

체스판의 정사각형을 나타내는 64개의 입력 변수를 정의합니다.각 변수는 해당 정사각형에 여왕이 있는지 여부를 나타냅니다.생각해 보세요.

• 특정 열에서는 변수가 하나만 "1"입니다.
• 특정 행에서 변수는 "1"뿐입니다.
• 특정 대각선에서 변수가 하나 또는 하나도 없는 경우 "1"입니다.

OBDD를 구축하면 해결할 수 있지만, ZDD를 사용하는 것이 효율적이며, 8-Queens 문제에 대한 ZDD를 구축하려면 S1에서 S8까지 8단계가 필요합니다.각 단계는 다음과 같이 정의할 수 있습니다.

첫 번째 줄에 퀸을 배치하는 모든 선택지를 나타냅니다.

S2: 첫 번째 여왕을 위반하지 않도록 두 번째 줄에 여왕을 배치하는 모든 선택 사항을 나타냅니다.

S3: 이전 퀸을 위반하지 않도록 세 번째 열에 퀸을 배치하는 모든 선택 사항을 나타냅니다.

…

S8: 이전 퀸을 위반하지 않도록 8번째 열에 퀸을 배치하는 모든 선택 사항을 나타냅니다.

S8용 ZDD는 8-Queens 문제의 모든 잠재적 해결책으로 구성됩니다.이 특정 문제의 경우 캐싱을 통해 알고리즘의 성능이 대폭 향상될 수 있습니다.캐시를 사용하여 중복을 방지하면 그림 10에 나타낸 것과 같이 기본 작업만 사용하는 경우보다 N-Queens 문제를 최대 4.5배 빠르게 개선할 수 있습니다.

기사의 여행 문제

기사단 투어 문제는 역사적 의미가 있다.기사 그래프에는 체스판의 정사각형을 묘사하기 위한 꼭지점 n2개가 포함되어 있습니다.모서리는 기사의 법적 움직임을 보여준다.기사는 게시판의 각 광장을 정확히 한 번 방문할 수 있습니다.Olaf Schröer, M. Löbing 및 Ingo Wegener는 그래프 상의 각 에지에 대해 부울 변수를 할당하고 모든 에지를 지정하는 총 156개의 변수를 할당함으로써 이 문제에 접근했습니다.문제의 해결은 156비트 조합 벡터로 나타낼 수 있다.Minato에 따르면, 모든 솔루션에 대한 ZDD 구축은 직접 해결하기에는 너무 큰 규모입니다.분열하고 정복하는 것이 더 쉽다.문제를 보드의 두 부분으로 나누고 하위 공간에 ZDD를 구성함으로써 64개의 엣지를 포함한 각 솔루션으로 더 나이트의 투어 문제를 해결할 수 있다.그러나 그래프가 매우 희박하지 않기 때문에 ZDD를 사용하는 이점은 그다지 명확하지 않습니다.

장애 시뮬레이션

N. Takahashi 등은 OBDD를 사용하여 여러 고장이 주어진 고장 시뮬레이션 방법을 제안했다.이 연역적 방법은 고장 세트를 1차 입력에서 1차 출력으로 전송하고 1차 출력에서 고장을 캡처합니다.이 메서드는 유니테 큐브 집합 식을 포함하므로 ZDD가 더 효율적입니다.단일 큐브 집합 계산에서 ZDD로부터의 최적화는 ZDD가 VLSI CAD 시스템 개발 및 기타 무수한 애플리케이션에서 유용할 수 있음을 나타냅니다.

「 」를 참조해 주세요.

• 순서 있는 바이너리 결정도(OBDD)
• 치환 결정도(ddDD)
• 시퀀스 결정도(SeqDD)
• 중요도(SDD)
• 그룹 의사결정도(GDD)

사용 가능한 패키지

• CUDD: BDD와 ZBDD를 구현하는 C로 작성된 BDD 패키지, 콜로라도 대학교, 볼더
• JDD, 일반적인 BDD 및 ZBDD 작업을 구현하는 Java 라이브러리
• Graphillion, Python 기반 ZDD 소프트웨어 구현
• [1], Donald Knuth의 CWEB ZDD 구현.

레퍼런스

추가 정보

• Minato, Shin-Ichi (1993). "Zero-suppressed BDDS for set manipulation in combinatorial problems". Proceedings of the 30th international on Design automation conference - DAC '93. pp. 272–277. doi:10.1145/157485.164890. ISBN 978-0-89791-577-9. S2CID 11096308.
• Ch. Meinel, T.Theobald, "VLSI-Design: OBDD – Foundations and Applications", Springer-Verlag, 베를린, 하이델베르크, 뉴욕, 1998.
• Minato, Shin-ichi (May 2001). "Zero-suppressed BDDs and their applications". International Journal on Software Tools for Technology Transfer. 3 (2): 156–170. doi:10.1007/s100090100038. hdl:2115/16895. S2CID 42919336.
• Bryant, R.E. (1995). "Binary decision diagrams and beyond: Enabling technologies for formal verification". Proceedings of IEEE International Conference on Computer Aided Design (ICCAD). pp. 236–243. doi:10.1109/ICCAD.1995.480018. ISBN 978-0-8186-7213-2. S2CID 62602492.
• 린, 벤"ZDDs" ZDDs - Stanford University, 2005, crypto.stanford.edu/pbc/notes/zdd/.
• Mishchenko, Alan (2001). "An Introduction to Zero-Suppressed Binary Decision Diagrams" (PDF). CiteSeerX 10.1.1.67.8986. S2CID 14216256. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
• 크누스, 도널드 EThe Art of Computer Programming, 제4권 2008년 12월 22일

외부 링크

• 린, 벤"ZDDs" ZDDs - Stanford University, 2005, crypto.stanford.edu/pbc/notes/zdd/
• Donald Knuth, Fun With Zero-Suppressed Binary Decision Diagram(ZDD) (비디오 강의, 2008)
• 미나토 신이치, 그래프에서의 패스 카운트(ZDD의 기초) (미라이칸에서 제작되는 비디오 일러스트)