가시성 폴리곤

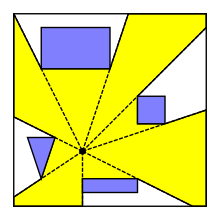
계산 기하학에서 장애물 중 평면의 p 지점에 대한 가시성 폴리곤 또는 가시성 영역은 p에서 볼 수 있는 평면의 모든 점의 가능한 무한 폴리곤 영역이다.가시성 폴리곤은 세그먼트 또는 폴리곤에서 가시성을 위해 정의할 수도 있다.가시성 폴리곤은 로봇공학, 비디오 게임, 그리고 미술관에 경비원을 가장 잘 배치하는 것과 같은 시설 위치를 결정하는데 유용하다.

가시성 폴리곤이 경계를 이루면 별 모양의 폴리곤이다.가시성 폴리곤은 해당 지점에서 발생하는 모든 광선이 결국 어떤 장애물에서 종료될 경우 경계된다.예를 들어 장애물이 단순한 폴리곤의 가장자리이고 p가 폴리곤 내부에 있는 경우 등이 여기에 해당한다.후자의 경우 가시성 다각형은 선형 시간에서 찾을 수 있다.^[1][2][3][4]

정의들

형식적으로 평면 가시성 폴리곤 문제를 이와 같이 정의할 수 있다.$S{\displaystyle }$ ${\displaystyle S}$을(를) ${\displaystyle {\mathrm{}}^{}}$ 2 ${\$^{$2}}$의 장애물(부분$$ 또는 다각형) 집합으로 하고$,$ $p{\displaystyle }$ ${\displaystyle p}$을(를) 장애물 내에 있지 않은$$ $R{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\$2}}의 지점으로 한다$$.그런 다음 점 가시성 $폴리곤{\displaystyle }$ V ${\displaystyle$ V$}$의 모든 점 $Q{\displaystyle }$ ${\displaystyle$ $q}$에 대해 세그먼트 $p{\displaystyle }$ ${\displaystyle q}$ ${\displaystyle pq}$이$($가) $S{\displaystyle }$ ${\displaystystyle S$의 어떤 장애물도$$ 교차하지 ${\displaystyle {\mathrm{}}^{}}$ R$$2 {\$displaystystyleb {R}$^{R}$$$^{$R}의 점 집합이다$$.

마찬가지로 세그먼트 가시성 폴리곤 또는 에지 가시성 폴리곤은 선 세그먼트를 따라 모든 점에서 볼 수 있는 부분이다.

적용들

가시성 다각형은 로봇공학에서 유용하다.예를 들어 로봇 국산화에서는 라이더와 같은 센서를 사용하는 로봇이 볼 수 있는 장애물을 감지해 가시성 다각형과 비슷하다.^[5]

그것들은 또한 비디오 게임에서도 유용하며, 그것을 구현하기 위한 간단한 알고리즘을 설명하는 수많은 온라인 자습서가 있다.^[6][7][8]

점 가시성 폴리곤 알고리즘

점 가시성 폴리곤 계산을 위해 수많은 알고리즘이 제안되었다.문제의 다른 변형(예: 다른 유형의 장애물)의 경우 알고리즘은 시간 복잡성에 따라 달라진다.

순진한 알고리즘

순진한 알고리즘은 이해하고 구현하기 쉽지만 다른 알고리즘보다 훨씬 느릴 수 있기 때문에 최적의 알고리즘은 아니다.

균일한 레이 주물 "물리적" 알고리즘

실생활에서 빛나는 점은 모든 방향에서 빛을 발산하기 때문에 그것이 보이는 영역을 비춘다.이것은 여러 방향으로 광선을 쏘면 시뮬레이션할 수 있다.점이 $p{\displaystyle }$ ${\displaystyle p}$이고 장애물 집합이 $S{\displaystyle }$ ${\displaystyle S}$이라고 가정해 보십시오. 그러면 다음과 같은 방법으로 유사점을 나타낼 수 있다$.$

algorithm naive_bad_algorithm(${\displaystyle p}$, ${\displaystyle S}$) is ${\displaystyle V}$ := ${\displaystyle \emptyset }$ for ${\displaystyle \theta =0,\cdots ,2\pi }$:         // shoot a ray with angle ${\displaystyle \theta }$ ${\displaystyle r}$ := ${\displaystyle$$S{\displaystyle }$ ${\displaystyle S}$의 각 장애물에 대한$$ $\inflt$$\}:$ r${\displaystyle }${\$displaystyle$ r$}=$min(${\displaystyle }$ ${\$$displaystyle$ $r$$},$ ${\displaystyle p}$ ${\\displaystyle$ $p$${\displaystyle \}}$에서 이 방향의 장애물까지의$$ 거리)을 V${\displaystyle }$${\$$displaystystyle V}$에 추가하십시오$.$

이제 무한히 많은 각도를 다 시도할 수 있다면 결과는 정확할 것이다.불행히도 컴퓨터의 한계 때문에 모든 방향을 실제로 시도한다는 것은 불가능하다.근사치는 예를 들어 50개의 광선을 균일하게 간격을 두고 주조하여 생성할 수 있다.그러나 작은 장애물이 인접한 두 개의 광선에 의해 완전히 놓칠 수 있기 때문에 이것은 정확한 해결책은 아니다.게다가, 대략 비슷한 해결책을 얻기 위해 많은 광선을 쏴야 할 수도 있고 출력 가시성 폴리곤에는 필요 이상으로 정점이 더 많을 수도 있기 때문에, 그것은 매우 느리다.

모든 꼭지점에 대한 레이 캐스팅

앞에서 설명한 알고리즘은 모든 장애물의 정점에 광선만 쏘는 것으로 충분하다는 관찰을 함으로써 속도와 정확성 모두에서 현저하게 향상될 수 있다.왜냐하면 가시성 폴리곤의 경계를 따라 구부러지거나 코너는 장애물에 있는 어떤 구석(즉, 꼭지점)에 기인해야 하기 때문이다.

알고리즘 순진_better_algorithm(${\displaystyle }$ ${\displaystyle$ $p$$\},$ $S{\displaystyle }$ ${\displaystyle S}$)은 ${\displaystyle S}$의 각$$ 장애물 $b{\displaystyle }$ ${\displaystyle b$$}$에 대해$$$$V ${\displaystyle$ $\$$empt$ $\}:/$shoot이다.$p{\displaystyle }$ ${\displaystyle$ $p}$에서 $v{\displaystyle }$ ${\$$displaystyle$ $v}$ r ${\displaystyle$ $r$$}$ :=$$$$ $S{\displaystyle }$ $\{\}$의 각 장애물 $b{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$$displaystyle p}$에 대한$$ $p{\displaystyle }$${\$$displaystyle v}$까지의 거리$\displaystyle$ $S$$}$: r ${\displaystyle r}$ :=$$$min{\displaystyle }$(${\displaystyle }$ ${\$$displaystyle$ $r$ p ${\$displaystyle $p}$에서 $\$ {\$displaystyle b$$'}$까지의 거리$)$에 정점$({\displaystyle }$ ( ,${\displaystyle r}$)을$$V ${\$$displaystyle$ V$}$에 추가한다$.$

위의 알고리즘은 정확하지 않을 수 있다.Talk 아래의 토론을 참조하십시오.

이 알고리즘의 시간 복잡성은 $O{\displaystyle }$( ${\displaystyle {n\mathrm{}}^{}}$ 2${\displaystyle {}^{}}$) ${\displaystyle O(n^{2})}$ 입니다$.$알고리즘이 $모든{\displaystyle }$ n$${\$displaystyle n$} 정점에$$ 레이를 쏘고, 레이가 끝나는 지점을 확인하려면 $O{\displaystyle (n)}$ ${\displaystyle O(n)$ 장애물$$ 하나와 교차하는지를 확인해야 하기 때문이다.이것은 비디오 게임과 같은 많은 간단한 어플리케이션에 충분하며, 그만큼 많은 온라인 자습서들이 이 방법을 가르치기 때문이다.^[8]그러나 나중에 보게 될 것처럼 더 빠른 $O{\displaystyle (n}$ ${\displaystyle \log \mathrm{logn}}$) ${\displaystyle O(n\log$ n$)}$ 알고리즘$$(또는 장애물이 단순한 다각형이거나 고정된 수의 다각형 구멍이 있는 경우 더 빠른 알고리즘)이 있다.

단순 폴리곤에서 점의 최적 알고리즘

간단한 다각형 $P{\displaystyle \mathcal{}}$ ${\$과 $점{\displaystyle }$ P ${\$$mathcal {\$$displaystyle p}$을(를) 감안할 때$,$ $p{\displaystyle }${\$displaystyle$p}에서 볼 수 있는$$ $P{\displaystyle \mathcal{}}${\$displaystystyle {p}$의 영역 계산에 선형 시간 알고리즘이 최적임$.$ 이러한 알고리즘은 1981년에 처음 제안되었다.^[2]하지만, 그것은 꽤 복잡하다.1983년에 개념적으로 간단한 알고리즘이 제안되었는데,^[3] 1987년에 수정된 사소한 오류가 있었다.^[4]

후자의 알고리즘은 여기서 간략하게 설명될 것이다.It simply walks around the boundary of the polygon ${\displaystyle {\mathcal {P}}}$, processing the vertices in the order in which they appear, while maintaining a stack of vertices ${\displaystyle {\mathcal {S}}=s_{0},s_{1},\cdots ,s_{t}}$ where ${\displaystyle s_{t}}$ is the맨 위스택은 $지금$까지 p$${\$displaystyle p}$에 보이는 정점을 구성한다$.$ 나중에 알고리즘을 실행하는 동안 $S{\displaystyle \mathcal{}}$ ${\$의 모호한 부분이 발견되면 $S{\displaystyle \mathcal{}}$ ${\$에서 모호한 정점이 튀어나올 것이다$.$겹겹이 쌓이다알고리즘이 종료될 때까지 $S{\displaystyle \mathcal{}}$ ${\$은(는) 모든 가시 정점, 즉 원하는 가시성 폴리곤으로 구성된다$$.효율적인 구현이 2014년에 발표되었다.^[9]

구멍이 있는 폴리곤의 점에 대한 최적의 알고리즘

$h{\displaystyle }$ ${\displaystyle h}$홀과$$ $n{\displaystyle }$ ${\displaystyle n}$ 정점이$$ 있는 폴리곤의 한 점에 대해서는 최악의 경우 $\theta {\displaystyle \mathrm{}(n}$+ ${\displaystyle h}$ ${\displaystyle \log }$ ${\displaystyle }$ ${\displaystyle h}$) ${\displaystyle \Theta(n+h\log h)}$ 알고리즘이$$ 최적임을 나타낼 수 있다.그러한 알고리즘은 그 최적성의 증명과 함께 1995년에 제안되었다.^[10]그러나 샤젤의 선형 시간 다각형 삼각측량 알고리즘에 의존하고 있어 극히 복잡하다.

세그먼트 중 한 점에 대한 최적의 알고리즘

끝점을 제외하고 교차하지 않는 세그먼트

$엔드포인트$를 제외하고 교차하지 않는 n ${\displaystyle n}$ 세그먼트$$ 집합 중 한 점에 대해서는 최악의 경우 $\theta {\displaystyle \mathrm{}(n}$ log${\displaystyle \mathrm{nn}}$) ${\displaystyle \Theta(n\log$ n$)}$ 알고리즘이$$ 최적임을 보여줄 수 있다.그 이유는 가시성 폴리곤 알고리즘이 가시성 폴리곤의 정점을 정렬된 순서로 출력해야 하기 때문에, 정렬의 문제는 가시성 폴리곤의 계산으로 줄어들 수 있기 때문이다.^[11]

세그먼트 중 한 점에 대한 가시성 폴리곤을 계산하는 알고리즘은 다른 모든 종류의 폴리곤 장애물에 대한 가시성 폴리곤을 계산하는 데 사용될 수 있다. 왜냐하면 모든 폴리곤은 세그먼트로 분해될 수 있기 때문이다.

분열시켜 정복하다.

가시성 다각형을 계산하기 위한 분할 및 분할 알고리즘은 1987년에 제안되었다.^[12]

각도 스위프

가시성 다각형을 계산하기 위한 회전 평면 스위프 알고리즘과 같은 각도 스위프는 1985년과^[13] 1986년에 제안되었다.^[11]아이디어는 먼저 모든 세그먼트 끝점을 극각으로 정렬하고, 그 순서대로 그 위에 반복하는 것이다.반복하는 동안 이벤트 라인은 힙으로 유지된다.효율적인 구현이 2014년에 발표되었다.^[9]

일반적으로 교차하는 세그먼트

일반적으로 교차하는 세그먼트 사이의 점의 경우 가시성 폴리곤 문제는 선형 시간 내에 하단 봉투 문제로 축소할 수 있다.다벤포트-신젤 인수에 따르면 최악의 경우 하단 엔벨롭에는 $vert{\displaystyle \mathrm{}(n}$ ${\displaystyle \alpha }$ (n${\displaystyle \Theta (n)}$의 정점 수가 있으며, 여기서 $\alpha {\displaystyle (n}$ ${\displaystyle )}$ ${\displaystyle \alpha (n)}$은 역 Ackermann 함수다.$in{\displaystyle \mathrm{}}$ (n ${\displaystyle \log }$ $){\displaystyle \Theta (n\log$ n$)}$ time으로$$ 실행되는 최악의 경우 분할 및 분할 알고리즘은 1989년에 John Hershberger에 의해 생성되었다.^[14]

참조

외부 링크

• http://web.informatik.uni-bonn.de/I/GeomLab/VisPolygon/index.html.en (단순 다각형으로 표시 - 애플릿)

소프트웨어

• VisiLibity:평면 폴리곤 환경에서 가시성 계산을 위한 무료 오픈 소스 C++ 라이브러리.
• 가시성-폴리곤-js: 각도 스위프 방법을 사용하여 세그먼트 중 한 점에 대한 가시성 다각형을 계산하기 위한 공용 도메인 Javascript 라이브러리.