정점 분리기

관련 항목
그래프 연결
연결성 대수연결성 사이클 순위 순위(그래프 이론) SPQR 트리 St-연결성 K-연결성증명서 픽셀 연결 정점 분리기 강하게 연결된 구성 요소 바이콘넥트 그래프 브릿지
v t

그래프 이론에서 정점 부분 집합 ${\displaystyle S}$$display$ V {\$displaystyle{\displaystyle }$ S\$subset V}$은 그래프에서$$ $S{\displaystyle }$ ${\$$displaystyle$ $S}$을(를) 분리하는 경우$$ ${\displaystyle a}$ $및{\displaystyle }$ b$$ ${\displaystyle b}$에 대한 정점 구분자$$(또는 정점 절단, 분리 세트)이다.간결하게 연결된 구성 요소.

예

r 행과 c 열이 있는 그리드 그래프를 생각해 보십시오. 정점의 총 개수 n은 r*c입니다. 예를 들어, 그림에서 r = 5, c = 8 및 n = 40. r이 홀수일 경우 중심 행이 하나 있고, 그렇지 않을 경우 중심과 똑같이 가까운 두 개의 행이 있다. 마찬가지로 c가 홀수일 경우 중심 열이 하나 있고, 그렇지 않을 경우 중심과 똑같이 가까운 두 개의 열이 있다. 이러한 중심 행이나 열 중 하나로 S를 선택하고 그래프에서 S를 제거하면 그래프를 두 개의 더 작은 연결된 하위 그래프 A와 B로 분할하는데, 각각 정점이 최대 n/2이다. r ≤ c (그림과 같이)인 경우, 중심 기둥을 선택하면 r n nn 정점이 있는 구분자 S가 표시되며, 마찬가지로 c r r의 경우 중심 행을 선택하면 최대 vertn 정점이 있는 구분자를 표시된다. 따라서 모든 그리드 그래프에는 최대 크기 separatorn의 구분자 S가 있으며, 이 구분자를 제거하여 각각 최대 크기 n/2인 두 개의 연결된 구성요소로 분할한다.^[1]

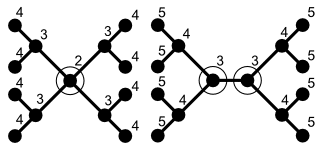
다른 종류의 예를 들어보자면, 모든 자유 트리 T에는 하나의 꼭지점으로 구성된 분리자 S가 있으며, 이 분리막 T를 최대 n/2의 크기로 두 개 이상의 연결된 구성 요소로 분리한다. 보다 정확히 말하면, 나무가 중심인지 바이크입력인지에 따라 항상 정확히 한 정점 또는 정확히 두 정점이 있는데, 이 정점은 그러한 구분자에 해당한다.^[2]

이러한 예와는 반대로, 모든 정점 분리기가 균형을 이루는 것은 아니지만, 그 속성은 평면 분리기 정리처럼 컴퓨터 과학의 응용에 가장 유용하다.

최소 구분자

S를 (a,b)-분리자, 즉 두 개의 비인접 정점 a와 b를 구분하는 정점 부분 집합으로 한다. S의 적절한 부분집합이 a와 b를 구분하지 않는 경우 S는 최소(a,b)-분리기가 된다. 보다 일반적으로 S는 일부 비인접 정점 쌍(a,b)에 대한 최소 구분자라면 최소 구분자라 불린다. 이는 정점 쌍(u,v)에 대해 S의 적절한 부분 집합이 최소(u,v)-분리기가 아니라는 최소 분리 집합과 다르다는 점에 유의하십시오. 다음은 최소 구분자를 특징짓는 잘 알려진 결과물이다.^[3]

Lemma. A vertex separator S in G is minimal if and only if the graph ${\displaystyle G-S}$, obtained by removing S from G, has two connected components ${\displaystyle C_{1}}$ and ${\displaystyle C_{2}}$ such that each vertex in S is both adjacent to some vertex in ${\displaystyle C_{1}}$ and to ${\displaystyle {C\mathrm{}}_{}}$ 2 ${\$}}개의 꼭지점$.$

최소 (a,b)"-분리기도 대수적 구조를 형성한다. 주어진 그래프 G의 두 고정 정점 a와 b에 대해, a에서 b까지의 모든 경로가 T를 충족하기 전에 S를 충족한다면, a (a,b)-분리자 S는 다른 (a,b)-분리자 T의 전신으로 간주될 수 있다. 보다 엄밀하게 말하면, 이전의 관계는 다음과 같이 정의된다. S와 T를 'G'에서 두 개(a,b)로 구분한다. 그 다음에 S는 기호 ${\displaystyle S_{}^{}}$ ${\displaystyle {}_{}^{}}$ a${\displaystyle {}_{}^{}}$, b ${\displaystyle G_{}^{}}$ $_{a,b}^{G}T$에서 각 $x{\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle S}$ ${\displaystyle \setminus }$ T ${\displaystyle x\in S\setminus T}$에 대해$$X를 B에 연결하는 모든 경로가 T와 만나는 경우 T의 전신이다. 이전 관계가 모든 (a,b) 구분자 집합에 대해 사전 순서를 산출한다는 정의에 따른다. 나아가 에스컬란테(1972)는 G에서 최소(a,b)-분리기의 집합으로 제한했을 때 전임자 관계가 완전한 격자를 발생시킨다는 것을 증명했다.

참고 항목

• 코드 그래프, 모든 최소 구분 기호가 클라이크인 그래프.
• k-35x 연결 그래프

메모들

참조

• Escalante, F. (1972). "Schnittverbände in Graphen". Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg. 38: 199–220. doi:10.1007/BF02996932.
• George, J. Alan (1973), "Nested dissection of a regular finite element mesh", SIAM Journal on Numerical Analysis, 10 (2): 345–363, doi:10.1137/0710032, JSTOR 2156361.
• Golumbic, Martin Charles (1980), Algorithmic Graph Theory and Perfect Graphs, Academic Press, ISBN 0-12-289260-7.
• Jordan, Camille (1869). "Sur les assemblages de lignes". Journal für die reine und angewandte Mathematik (in French). 70 (2): 185–190.
• Rosenberg, Arnold; Heath, Lenwood (2002). Graph Separators, with Applications. Springer. doi:10.1007/b115747.