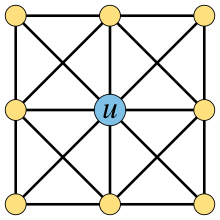
범용 꼭지점
Universal vertex그래프 이론에서 범용 꼭지점은 그래프의 다른 모든 정점에 인접한 비방향 그래프의 정점이다.그래프에 설정된 하나의 원소 지배를 형성하기 때문에 지배 정점이라고도 할 수 있다.(그래프의 논리에서 보편적으로 정량화된 정점과 혼동해서는 안 된다.)
보편적 꼭지점을 포함하는 그래프를 원추형이라고 할 수 있다.이런 맥락에서 보편적 꼭지점은 원뿔의 정점이라고도 할 수 있다.[1]그러나 이 용어는 정점이 평면 하위 그래프를 남기는 정점인 정점 그래프의 용어와 상충된다.
그래프의 특수 패밀리
별은 정확히 보편적인 꼭지점을 가진 나무로, 독립된 집합에 보편적인 꼭지점을 추가하여 만들 수도 있다.마찬가지로 휠 그래프는 사이클 그래프에 범용 꼭지점을 추가함으로써 형성될 수 있다.[2]기하학에서 3차원 피라미드는 바퀴 그래프를 골격으로 가지고 있으며, 보다 일반적으로 고차원 피라미드의 그래프는 피라미드의 정점으로서 보편적인 정점을 가지고 있다.
소소하게 완벽한 그래프(순서-이론적 나무의 비교가능성 그래프)는 항상 나무의 뿌리인 보편적 꼭지점을 포함하고 있으며, 더 강하게는 연결된 모든 유도 하위그래프가 보편적 꼭지점을 포함하는 그래프로 특징지어질 수 있다.[3]연결된 분계점 그래프는 미미하게 완벽한 그래프의 하위 클래스를 형성하므로 범용 꼭지점을 포함하기도 한다. 범용 꼭지점 또는 절연된 꼭지점(사건 가장자리가 없는 그래프)을 반복적으로 추가하여 구성할 수 있는 그래프로 정의할 수 있다.[4]
보편적 꼭지점이 있는 모든 그래프는 해체 가능한 그래프로, 닫힌 이웃이 다른 정점의 부분 집합인 정점을 반복적으로 제거하면 정점을 하나의 정점으로 줄일 수 있다는 것을 의미한다.다른 모든 정점을 제거하고 모든 정점을 제거하는 모든 제거 순서는 이 정의에 적합하다.거의 모든 해체 가능한 그래프는 보편적인 정점을 가지고 있는 -vertex 해체 가능한 그래프의 이 무한대로 가면서 한계에서 하나가 되는 경향이 있다는 점에서 보편적인 정점을 가지고 있다.[5]
그래프의 강한 산물에서 지배 횟수가 최대 곱절까지 증가한다는 관찰의 특별한 경우로서,[6] 강한 제품은 두 요인이 모두 증가한다면 그리고 그 두 가지 요인이 모두 증가한다면 만능 정점을 가진다.
인식
정점이 n개인 그래프에서 범용 꼭지점은 정확히 n - 1인 정점이다.따라서 분할 그래프와 마찬가지로 범용 꼭지점이 있는 그래프는 그래프의 구조를 보지 않고도 순전히 도 시퀀스에 의해 인식될 수 있다.
보편적 꼭지점을 갖는 속성은 그래프의 1차 논리학에서 공식으로 표현할 수 있다.그래프에서 인접 관계를 나타내기 위해~ 을(를) 사용하는 그래프 은 공식을 모형화하는 경우에만 범용 꼭지점을 가진다.
참조
- ^ Larrión, F.; de Mello, C. P.; Morgana, A.; Neumann-Lara, V.; Pizaña, M. A. (2004), "The clique operator on cographs and serial graphs", Discrete Mathematics, 282 (1–3): 183–191, doi:10.1016/j.disc.2003.10.023, MR 2059518.
- ^ Bonato, Anthony (2008), A course on the web graph, Graduate Studies in Mathematics, vol. 89, Atlantic Association for Research in the Mathematical Sciences (AARMS), Halifax, NS, p. 7, doi:10.1090/gsm/089, ISBN 978-0-8218-4467-0, MR 2389013.
- ^ Wolk, E. S. (1962), "The comparability graph of a tree", Proceedings of the American Mathematical Society, 13: 789–795, doi:10.2307/2034179, MR 0172273.
- ^ Chvátal, Václav; Hammer, Peter Ladislaw (1977), "Aggregation of inequalities in integer programming", in Hammer, P. L.; Johnson, E. L.; Korte, B. H.; Nemhauser, G. L. (eds.), Studies in Integer Programming (Proc. Worksh. Bonn 1975), Annals of Discrete Mathematics, vol. 1, Amsterdam: North-Holland, pp. 145–162.
- ^ Bonato, Anthony; Kemkes, Graeme; Prałat, Paweł (2012), "Almost all cop-win graphs contain a universal vertex", Discrete Mathematics, 312 (10): 1652–1657, doi:10.1016/j.disc.2012.02.018, MR 2901161.
- ^ Lakshmanan, S. Aparna; Vijayakumar, A. (2009), "A note on some domination parameters in graph products", Journal of Combinatorial Mathematics and Combinatorial Computing, 69: 31–37, MR 2517304
- ^ Fomin, Fedor V.; Golovach, Petr A.; Thilikos, Dimitrios M. (2021), "Parameterized complexity of elimination distance to first-order logic properties", 36th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2021, Rome, Italy, June 29 - July 2, 2021, IEEE, pp. 1–13, arXiv:2104.02998, doi:10.1109/LICS52264.2021.9470540